GPS, ćwiczenia

GNSS - Globalne Nawigacyjne Systemy Satelitarne [2012.11/2013.01 - 1]

(wprowadzenie dla studentów kursu ETP na III semestrze studiów)

GPS a GNSS

W codziennym użyciu posługujemy się określeniem „GPS” [„ gie-pe-es”] w odniesieniu do powszechnie dostęp-

nej nawigacji satelitarnej, gdy tymczasem bardziej właściwym terminem jest dziś „GNSS”, obejmujący wszystkie ak-

tualnie istniejące i budowane Globalne Nawigacyjne Systemy Satelitarne, a to (w kolejności zaawansowania):

a) zbudowany i nadzorowany przez USA, w pełni operacyjny od stycznia 1994 r. system NAVSTAR GPS;

b) zbudowany przez ZSRR, zrekonstruowany przez Rosję, w pełni operacyjny od jesieni 2011 r. GLONASS;

c) budowany przez Chiny system COMPASS (modyfikacja wcześniejszego systemu BEIDOU; wg komunikatu z

grudnia 2011 r. Beidou osiągnął lokalną operacyjność na obszarze Chin i terytoriach przyległych);

d) budowany przez Japonię system QZSS (Quasi Zenith Satellite System), o zasadzie działania podobnej do Beidou;

e) budowany przez UE system GALILEO;

f) system projektowany przez Indie.

2. Nawigacja przed powstaniem GNSS

Podstawowym impulsem projektowania i budowy GNSS były potrzeby militarne okresu „zimnej wojny”, gdyż

znane i stosowane do lat 60-tych XX wieku systemy nawigacyjne nie odpowiadały możliwościom i potrzebom stale

ulepszanych rodzajów broni, a tym bardziej wprowadzanych nowości: atomowych łodzi podwodnych o praktycznie

nieograniczonym zasięgu, rakiet balistycznych, lotnictwa strategicznego i pocisków samosterujących.

Przypomnijmy: sposoby wyznaczania szerokości geograficznej na podstawie obserwacji wysokości Słońca

i gwiazd nad horyzontem były znane już w starożytności. Cztery wieki przed naszą erą szerokość geograficzna Mar-

sylii była znana greckim żeglarzom z błędem poniżej 30΄ (55 km), a Eratostenes w III w. p.n.e., znając odległość

dzielącą dwa punkty leżące na jednym południku, wyznaczył promień Ziemi na podstawie pomierzonej różnicy sze-

rokości geograficznych tych punktów dokładniej, niż zrobiono to w Europie w XVIII w. Niemal do połowy XX w.

wyznaczenie szerokości geograficznej statku na otwartym morzu, wykonywane za pomocą sekstansu, nie było moż-

liwe z błędem mniejszym niż 0.3º-0.5º (ok. 35-55 km w łuku południka), choć dzięki postępom astronomii i roz-

wojowi instrumentów dokładność wyznaczenia szerokości geograficznej punktu na stałym lądzie już w XIX w. osią-

gnęła poziom 0.1″-0.2″ (ok. 3-6 m). O wiele trudniejsze było wyznaczenie długości geograficznej, wymagające trans-

feru czasu. Na statku zliczanie przebytej trasy dawało w najlepszym przypadku błąd rzędu kilkunastu procent; dopie-

ro wprowadzony w 1761 r. chronometr Harrisona, zegar sprężynowy niewrażliwy na kołysanie, pozwolił na popra-

wienie dokładności wyznaczenia długości geograficznej do niecałej mili morskiej (1΄ łuku południka) po nawet

dwóch miesiącach żeglugi. W przypadku obserwatoriów lądowych było niewiele lepiej: równoczesne obserwacje

zjawisk astronomicznych - najczęściej przesłonięć gwiazd przez Księżyc lub zaćmień księżyców Jowisza - dawały

niewiele wyższe dokładności. Oczywiście wyznaczenia pozycji były możliwe tylko wówczas, gdy Słońca lub obser-

wowanych gwiazd nie zasłaniały chmury.

Przełom przyniósł początek XX wieku – w 1901 r. G. Marconi dokonał pierwszej transmisji sygnału radiowego

przez Atlantyk. Radio umożliwiło precyzyjną – już na początku przynajmniej na poziomie 0.01s – synchronizację ze-

garów na całej kuli ziemskiej, i tym samym dokładność wyznaczenia długości geograficznej obserwatoriów zrównała

się z dokładnością wyznaczenia ich szerokości. Radio umożliwiło też budowę zupełnie nowego rodzaju systemów

nawigacyjnych, których szczególny rozkwit nastąpił w okresie II wojny światowej. Niektóre z nich, tzw. hiperbolicz-

ne, w których pozycja była wyznaczana na podstawie różnic czasu recepcji sygnałów radiowych, emitowanych przez

przynajmniej dwie pary nadajników umieszczonych w punktach o znanych współrzędnych, pozwalały na wyznacze-

nie pozycji statku lub samolotu w strefie przybrzeżnej z dokładnością rzędu kilkuset metrów. Na szczególną uwagę

zasługują tu systemy: Loran, Omega i – wyjątek – całkowicie cywilna Decca, które służyły żeglarzom przez wiele

powojennych dziesięcioleci.

Systemy oparte na propagacji fal radiowych pozwoliły na nieprzerwane wyznaczanie pozycji, nawigację w każ-

dych warunkach pogodowych, jednakże emisja sygnałów z naziemnych źródeł powodowała niejednoznaczność ich

przebiegu: wzdłuż zakrzywionej powierzchni Ziemi lub w serii odbić od tej powierzchni i od jonosfery, i tym samym

niejednoznaczność wyznaczanych pozycji.

Kolejny przełom nastąpił 04 października 1957 r. Przyniosło go wystrzelenie przez ZSRR pierwszego sztuczne-

go satelity Ziemi – Sputnika-1. Nadawany przez Sputnika sygnał radiowy dobiegał do odbiorników naziemnych po

linii prostej i był doskonale odbieralny na wielkich obszarach, pomimo wywołanych efektem Dopplera zmian odbie-

ranej częstotliwości. Analizując odbierane sygnały, niemal natychmiast na całym świecie zdano sobie sprawę, że pre-

cyzyjna globalna nawigacja będzie możliwa tylko przy zastosowaniu systemów satelitarnych.

Pierwsze rozwiązania wykorzystywały właściwości efektu Dopplera. Zrównanie częstotliwości odbieranej przez

naziemny odbiornik z nominalną (emitowaną przez satelitę) następowało w momencie, gdy (pomijając nieistotne w

tym przypadku efekty relatywistyczne) zarówno odbiornik jak i satelita znalazły się w płaszczyźnie prostopadłej do

wektora chwilowej prędkości satelity. Równocześnie widoma prędkość zmian odbieranej częstotliwości pozwalała

wyznaczyć odległość odbiornika od satelity. Znajomość tych dwóch parametrów, wraz ze znajomością parametrów

orbity satelity, pozwalała, po odebraniu sygnałów z kilku satelitów, na wyznaczenie pozycji okrętu w ruchu w do-

wolnym miejscu oceanu światowego z kilkusetmetrową niepewnością. Na lądzie stałym jedno-dwudobowe rejestra-

cje prowadzone przez nieruchomy odbiornik już połowie lat 70-tych XX w. pozwalały na wyznaczenie jego pozycji

w każdych warunkach pogodowych z kilkumetrowym błędem (a więc była to dokładność porównywalna z dokładno-

ścią wyznaczeń astronomicznych, jednakże wolna od wpływu lokalnych odchyleń pionów), ale już różnica pozycji

dwóch odbiorników, wyznaczana symultanicznym pomiarem, była obarczona błędem rzędu 1 - 2 m niezależnie od

tego, czy odbiorniki były odległe od siebie o kilka metrów czy kilkaset kilometrów.

Systemy dopplerowskie umożliwiły wystarczająco precyzyjną nawigację flot, mogły wspomagać siły lądowe,

jednakże - z powodu długiego czasu potrzebnego do zebrania niezbędnej ilości danych - całkowicie nie odpowiadały

potrzebom lotnictwa i wojsk rakietowych. W zastosowaniach cywilnych zrewolucjonizowały geodezję wyższą,

umożliwiły precyzyjne wzajemne nawiązanie odległych wysp i kontynentów, a także wyznaczenie parametrów

kształtu Ziemi z nieosiągalną wcześniej dokładnością. Opracowany w latach 60-tych w USA system TRANSIT i

niewiele późniejsza radziecka TSIKADA („Cykada”) zostały w latach 70-tych udostępnione użytkownikom cywil-

nym. Pozostały w użyciu niemal do końca XX w., stopniowo ustępując miejsca dopiero systemom typu GNSS.

3. NAVSTAR GPS - początki.

Systemy hiperboliczne i dopplerowskie oraz wspomagające je systemy bezwładnościowe (nie omawiane w tym

kursie, wykorzystujące przyspieszeniomierze i żyrokompasy) nie zaspokajały potrzeb ani sił zbrojnych USA, ani

użytkowników cywilnych. Z tego powodu lotnictwo, marynarka i wojska lądowe próbowały już w latach 60-tych XX

w. budować własne systemy nawigacji satelitarnej. Poszukiwanie oszczędności wymusiło połączenie sił, doświad-

czeń i celów w jeden wspólny program. W pierwszy weekend września 1973 roku zebrał się zespół Joint Program

Office (Biuro Programu Wspólnego), którego uczestnicy, przedstawiciele wszystkich rodzajów sił zbrojnych USA

oraz NATO i pracujących dla wojska placówek badawczych, także cywilnych, podjęli fundamentalne decyzje okre-

ślające przyszły system nawigacji satelitarnej. Przede wszystkim sformułowano warunki, jakie nowy system miał

spełniać:

a) dostępność nieprzerwanie na całej kuli ziemskiej (24h/7d, 360º/±90º),

b) dostępność w każdych warunkach atmosferycznych,

c) umożliwienie trafienia 5 bomb i pocisków, zrzucanych lub wystrzeliwanych z różnych platform, w koło o śred-

nicy 10 m,

d) koszt pojedynczego odbiornika poniżej 10 tyś. USD (w cenach 1973 r.; ostatnie zdanie mieli księgowi ...).

Podejmując decyzję o budowie systemu GPS spełniającego te warunki, wykorzystano dotychczasowe doświad-

czenia: z systemu TRANSIT przejęto metody predykcji parametrów orbit, sposób eliminacji wpływu jonosfery oraz –

ważne na tym pionierskim etapie! – przekonanie o wykonalności i sensowności całego zadania. Budowane przez ma-

rynarkę satelity TIMATION wniosły doświadczenie z pracą zegarów atomowych w przestrzeni kosmicznej, a ostatni

z tych satelitów – NTS-II (zwany też Timation III) – posłużył do pierwszych testów praktycznych. Z programu 621B

lotnictwa przejęto projekt konstelacji oraz doświadczenie z pomiarami odległości do satelitów za pomocą fal radio-

wych modulowanych specjalnymi, binarnymi pseudolosowymi kodami, zdefiniowanymi w taki sposób, że wszystkie

satelity mogły pracować na tej samej częstotliwości fali nośnej. W uproszczeniu możemy przyjąć, że kody niosą

wskazania zegara satelity.

Projekt uzyskał ostateczną akceptację Departamentu Obrony USA (DoD) 17 grudnia 1973 r. i został skierowany

do realizacji. Pełną operacyjność osiągnął w styczniu 1994 roku i od tego czasu pracuje nieprzerwanie.

W wyniku decyzji podjętych we wrześniu 1973 r. podstawową techniką nawigacyjną systemu NAVSTAR GPS

(„NAVSTAR the Global Positioning System”), służącą wyznaczeniu pozycji użytkownika, jest jednokierunkowy, fa-

zowy pomiar odległości od (przynajmniej) czterech satelitów o znanych pozycjach.

4. GNSS – wyznaczenie pozycji nawigacyjnej

Przypomnijmy: w klasycznej geodezji pomiar odległości między punktami A i B za pomocą fazowego dalmierza

elektronicznego przebiega następująco: nad punktem A (rys. 1) centrujemy dalmierz D, zaś nad punktem B reflektor

(pryzmat dalmierczy) R. Po wzajemnym nakierowaniu dalmierza i reflektora inicjujemy pomiar, w czasie którego

D R

Rys. 1. Pomiar odległości AB dalmierzem elektronicznym

dalmierz emituje ciągłą falę elektromagnetyczną zwykle z zakresu głębokiej czerwieni – bliskiej podczerwieni

(λn ≈ 0.68÷0.86 µ). Jest to fala nośna, modulowana amplitudowo sinusoidalną falą pomiarową o niższej częstotli-

wości, zwykle z przedziału 50 – 300 MHz, co odpowiada długościom fali λ ≈ 6.0÷1.0 m,. Po odbiciu przez reflektor

fala powraca do dalmierza, w którym, w procesie korelacji fali emitowanej i powracającej, następuje pomiar różnicy

ich faz ∆φ. Tak więc ukośną, jeszcze niezredukowaną o wpływy atmosfery i parametry kalibracyjne, odległość Du

pomiędzy centrem elektronicznym dalmierza i centrem optycznym reflektora możemy przedstawić wzorem:

(1)

u =

( N + ϕ

∆ )

gdzie N oznacza nieznaną ilość pełnych odłożeń fali, ∆φ pomierzoną różnicę faz, a współczynnik ½ wynika z faktu,

że fala przebiega odległość Du dwukrotnie. Liczba całkowita N jest nazywana niejednoznacznością odległości: trzy

różne Du równe odpowiednio 4.275 m, 145.275 m i 1273.275 m są nierozróżnialne przy pomiarze z falą modulującą

λ=6.0 m, gdyż wszystkie dają w wyniku dzielenia przez λ/2 tę samą resztę 1.275 m. Różnica faz ∆φ, tu mierzona

w zakresie [0 - 1), jest taka sama dla wszystkich tych trzech odległości i równa 0.4250. Wartości niejednoznaczności

N – dla naszych przykładowych odległości będą to odpowiednio N = 1, 48 i 424 – najczęściej wyznacza się wykonu-

jąc dodatkowe pomiary przy innych długościach fali modulującej λ.

Przyjrzyjmy się opisanemu wyżej trybowi pomiaru:

a) dalmierz „wie”, gdzie jest pryzmat, bo musi zostać nań nacelowany;

b) pryzmat „wie”, gdzie jest dalmierz, bo musi zostać skierowany w jego stronę;

c) pryzmat ujawnia swoją obecność, reemitując (tu: odbijając) wysyłaną przez dalmierz falę;

d) pomiar różnicy faz jest wykonywany w dalmierzu, z wykorzystaniem jego zegara;

e) pomiar odległości jest wykonywany na kilku (trzech lub więcej) częstotliwościach modulacji w celu wyznaczenia

niejednoznaczności N;

f) starannie dobrana fala nośna z pogranicza zakresu widma widzialnego i bliskiej podczerwieni korzystnie przenika

przez atmosferę;

Żadna z tych cech pomiaru klasycznego nie może się odnosić do wojskowego systemu nawigacji satelitarnej!

Choć zasada działania jest podobna, to zarówno warunki pomiaru, szczegóły jego realizacji jak i cele są odmienne:

ad a) satelita nigdy nie będzie „wiedział”, gdzie znajduje się próbujący określić swą pozycję żołnierz czy użytkownik

cywilny, a więc wiązka promieniowania emitowanego przez satelitę musi objąć całą Ziemię i to jeszcze z naddat-

kiem dla nawigacji samolotów i satelitów na niskich orbitach okołoziemskich (LEO, Low Earth Orbit);

ad b) żołnierz nie będzie wiedział, w którą stronę zwrócić antenę odbiornika, na dodatek, jak się za chwilę okaże, do

wyznaczenia pozycji będzie mu potrzebny odbiór sygnałów z przynajmniej czterech satelitów równocześnie;

ad c) żołnierz nie może ujawnić swojej pozycji emitując czy reemitując jakiekolwiek sygnały, gdyż zostałby wtedy

wykryty przez przeciwnika – sygnał musi przebiegać jednokierunkowo, od satelity do odbiornika żołnierza;

ad d) jednokierunkowy przebieg sygnału powoduje, że w pomiarze różnicy faz sygnału emitowanego przez satelitę i

sygnału odbieranego przez użytkownika muszą być zastosowane dwa różne zegary: zegar satelity i zegar odbior-

nika; prędkość fali radiowej wymusza synchronizację tych zegarów z niepewnością rzędu kilku nanosekund.

ad e) na podstawie doświadczeń programu 621B przyjęto inny sposób wyznaczania liczb N, czyli niejednoznaczności

odległości, choć właściwości atmosfery Ziemi i tak wymusiły pomiar na przynajmniej dwóch częstotliwościach;

ad f) sygnał satelitarny, z konieczności o niewielkiej mocy (moc nadajników pojedynczego satelity GPS to zaledwie

kilkadziesiąt W), musi przeniknąć przez atmosferę aż do jej powierzchni: nie może zostać zaabsorbowany przez

swobodne elektrony i zjonizowany gaz w jonosferze, ani przez parę wodną w troposferze, nie mówiąc już o zasło-

nięciu przez chmury, mgły czy deszcz. Użyteczne „okno” jest wąskie, obejmuje w przybliżeniu zakres częstotli-

wości 1 ÷ 2 GHz (co odpowiada falom o długości 30 ÷ 15 cm), i od dawna nie ma już w nim wolnych pasm.

Tak więc równanie (1) dla odległości satelity S od odbiornika A, wyznaczanej za pomocą GNSS (rys. 2), przyjmie

postać (zgodnie z tradycją wskaźniki odnoszące się do satelitów będziemy pisali u góry, a odnoszące się do obiektów

naziemnych – u dołu symboli):

ρ = λ( S

N + ϕ

∆ ) (2) O

Tę samą odległość możemy jednakże przedstawić jako iloczyn prędkości fali elektromagnetycznej w próżni

(co jest prawdziwe dla >95% tej odległości) i czasu przebiegu, a także w postaci analitycznej w pewnym, trójwymia-

rowym, geocentrycznym układzie współrzędnych prostokątnych:

satelita S

z ρ odległość geometryczna, ρ = cτ =

( x − x ) + ( y − y ) + ( z − z ) (3)

odbiornik A

Rys. 2. Pomiary satelitarne, wektor łączący satelitę GNSS i odbiornik.

Przyjmijmy oznaczenia:

' S

= − δ

t - czas GPS emisji sygnału przez satelitę, zegar satelity pokazuje wtedy t

t (4)

- czas GPS odbioru sygnału, zegar odbiornika pokazuje wtedy t = t − t

δ (5)

wówczas, dla uproszczenia pomijając chwilowo opóźnienie atmosferyczne i inne zakłócenia:

= cτ = c(

t − t ) (6) A

W czasie pomiaru nie znamy odchyłek chodów zegarów satelity δ t i odbiornika δ t , tak więc bezpośredniemu

pomiarowi podlega pseudoodległość oznaczana d :

d = c( '

' S

t − t ) = c(

t − δ t − t + δ t ) = c(

t − t ) − c(

δ t − δ t )

= ρ − c(

δ t − δ t ) (7)

Informacja o błędzie zegara satelity δ t , zawarta w „depeszy nawigacyjnej”, nadawanej przez satelitę dodatkowo,

oprócz kodów pomiarowych, jest wystarczająco dokładna dla nawigacyjnego wyznaczania pozycji i dlatego ten błąd

teraz pominiemy (choć powróci, już jako resztowy błąd, w pomiarach fazowych):

' S

d = c t

(

− t ) = ρ − cδ t = ( x − x ) + ( y − y ) + ( z − z 2

) − cδ t (8)

Powyższe równanie pseudoodległości (8) jest podstawowym równaniem służącym do wyznaczania pozycji w GNSS.

Widzimy je tutaj w niejako „kanonicznej” formie, nie uwzględniającej spowolnienia fali elektromagnetycznej w at-

mosferze i wpływu innych czynników zakłócających.

Jednoznaczne wyznaczenie czterech niewiadomych x , y , z oraz δ t wymaga rozwiązania układu czte-

rech równań typu (8), a więc rejestracji sygnałów emitowanych przez cztery różne satelity. Każdy doświadczony

geodeta natychmiast zda sobie sprawę, że geometria rozmieszczenia satelitów i ich ilość będą decydowały o dokład-

ności wyznaczenia pozycji odbiornika. Obecność obserwacji nadliczbowych (wykorzystanie sygnałów odebranych z

więcej niż 4 satelitów) pozwoli na wyrównanie obserwacji, a przez to uwierzytelnienie wyniku i ocenę dokładności

wyznaczonej pozycji.

Pozycję wyznaczoną na drodze rozwiązania układu równań typu (8) określamy jako bezwzględną: wyznacza ją

w konkretnym geocentrycznym układzie współrzędnych pojedynczy odbiornik, korzystający wyłącznie z zarejes-

trowanych przez siebie sygnałów satelitarnych, bez pomocy jakichkolwiek danych z innych źródeł. Z tychże powo-

dów nazywamy ją też pozycją autonomiczną. Inne stosowane określenie to pozycja nawigacyjna - jej wyznaczenie

jest spełnieniem założeń GNSS jako systemów globalnej nawigacji.

Tak pracują najprostsze odbiorniki turystyczne i nawigacyjne, z nawigacją samochodową włącznie, a także woj-

skowe. Jednakże w rzeczywistych wyznaczeniach uwzględnia się wpływ atmosfery (zwłaszcza jonosfery). Wyzna-

czenie pozycji odbiornika na drodze rozwiązania układu równań pseudoodległości z uwzględnieniem wpływów at-

mosfery spełnia wymogi stawiane systemom GNSS przez użytkownika wojskowego.

5. GNSS – poszukiwanie wyższej dokładności – wyznaczenie pozycji różnicowej kodowej

Głównymi źródłami błędów w wyznaczeniu bezwzględnym (pomijając niedoskonałości odbiornika) są: niezna-

jomość opóźnienia atmosferycznego oraz niedokładność wyznaczenia pozycji satelitów na podstawie przewidywa-

nych parametrów orbit (te przewidywane parametry nadaje każdy satelita we wspomnianej już depeszy satelitarnej).

Charakter tych źródeł powoduje, że wartości błędów są silnie skorelowane przestrzennie. Można wpływy tych błę-

dów zredukować, jeśli w sąsiedztwie będzie pracował inny odbiornik ustawiony na punkcie o znanych współrzęd-

nych. Nazwiemy go odbiornikiem bazowym lub referencyjnym i oznaczymy B. Znajomość własnych współrzęd-

nych, a tym samym możliwość obliczenia odległości do satelity ρ , pozwoli mu wyznaczyć odchyłki pomiarów po-

szczególnych pseudoodległości d obarczonych pełną listą błędów (wpływu atmosfery, parametrów orbit, zegarów

itp.):

∆

= d − ( x − x ) + ( y − y ) + ( z − z ) (9) B

Dzięki przestrzennemu skorelowaniu właściwości atmosfery i dużej odległości satelitów od powierzchni Ziemi,

odchyłki te są praktycznie takie same w promieniu nawet kilkuset kilometrów od stacji bazowej (przyjmuje się, że

ich niepewność wzrasta mniej więcej o 1 m/100 km). Wzięte z przeciwnym znakiem mogą być wykorzystywane jako

poprawki (korekcje) do pseudoodległości wyznaczanych przez inne odbiorniki, pracujące w tak szerokim sąsiedztwie

stacji referencyjnej. Dostarczane w trybie czasu rzeczywistego drogą radiową, przez łącza telefonii komórkowej lub

internet, pozwalają na dokładną bieżącą nawigację, zaś dołączone do plików danych przeznaczonych do postpro-

cessingu pozwalają na obliczenie poprawionych pozycji na etapie prac kameralnych. Pozycja wyznaczana przez od-

biornik nawigacyjny korzystający z tych poprawek nie jest już jednak pozycją bezwzględną, lecz względną, różnico-

wą. Systemy służące do wyznaczania pozycji różnicowej nazywamy DGPS (Differential GPS, ogólniej DGNSS).

Podany schemat opisuje najprostszą postać DGNSS. Pojedyncza stacja bazowa może obsługiwać odbiorniki tylko

jednego użytkownika lub wszystkie pracujące w określonym regionie; systemy rozmieszczonych co kilkaset kilome-

trów stacji bazowych dostarczają dziś uśrednione i interpolowane dane korekcyjne na obszar całych kontynentów:

przykładowo WAAS (Wide Area Augmentation System) dla USA i znacznych przyległych obszarów Kanady i Mek-

syku, EGNOS (European Geostationary Navigation Overlay Service) dla Europy i północnej Afryki, GAGAN dla In-

dii, SNAS dla Chin czy MSAS dla Japonii. Dzięki danym przekazywanym ze stacji referencyjnej w systemach

DGNSS, odbiorniki nawigacyjne uzyskały zdolność wyznaczania pozycji różnicowej z niepewnością 1-2 m w po-

ziomie, a odbiorniki o szczególnej konstrukcji, w pewnych warunkach, nawet z niepewnością rzędu 0.2 -0.3 m.

Z oczywistych przyczyn działanie w trybie różnicowym nie nadaje się do zastosowań wojskowych: stacja refe-

rencyjna emituje, w taki czy inny sposób, sygnały elektromagnetyczne, a więc może zostać natychmiast wykryta i, w

warunkach konfliktu zbrojnego, w ciągu najwyżej kilkunastu minut zniszczona. Zastosowania cywilne, dzięki lepszej

niż w trybie autonomicznym dokładności, są jednakże ogromne: od GIS, przez precyzyjne rolnictwo, precyzyjną na-

wigację lądową, śródlądową i morską, aż po systemy precyzyjnego lądowania samolotów.

Niestety, również z oczywistych przyczyn te w najlepszym razie kilkudecymetrowe dokładności nie zadowalają

geodetów.

GNSS – realizacja różnicowa fazowa

Już pierwsze doświadczenia cywilne z rejestracją sygnałów emitowanych przez satelity GPS wykazały, że moż-

liwa jest rejestracja nie tylko faz kodów (na podstawie których odbiornik poznaje czas nadania t sygnału, niezbęd-

ny do wyznaczenia pseudoodległości), ale także faz fal nośnych, na których te kody są modulowane.

Połączenie rejestracji faz fal nośnych, dobiegających do odbiornika od przynajmniej czterech satelitów, z ideą

różnicowego wyznaczania pozycji, dało w efekcie dokładności satysfakcjonujące geodetów. Składowe wektora ∆AB

różnicy pozycji dwóch punktów, na których przez odpowiednio długi czas równocześnie pracują i symultanicznie

wykonują odczyty faz fal nośnych dwa odbiorniki GNSS klasy geodezyjnej, mogą być dziś wyznaczane z niepewno-

ścią nie przekraczającą pojedynczych milimetrów, nawet jeśli te punkty są oddalone od siebie o tysiące kilometrów.

Technika pozwalająca uzyskiwać te fantastyczne dokładności jest dziełem użytkowników cywilnych. Jej szczegóły

podlegają ciągłej ewolucji mającej na celu uproszczenie i optymalizację pomiarów i obliczeń. Jak mówi znane wśród

geodetów wykonujących pomiary z wykorzystaniem GNSS porzekadło, ograniczenia zastosowań GNSS wynikają

tylko z ograniczeń naszej wyobraźni.

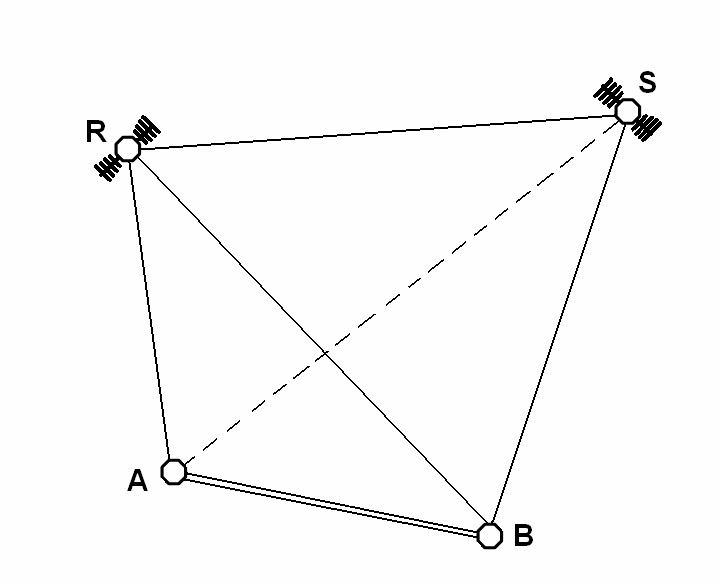
Rozpatrzmy przypadek, w którym sygnały nadawane przez dwa satelity R i S są rejestrowane równocześnie

przez dwa odbiorniki umieszczone w punktach A i B. Wyznaczeniu podlega wspomniany wyżej wektor ∆AB :

→

∆ = ∆

∆

−

( x

, y

, z

)

( x

x , y

y , z

z ) (10)

Rys. 3. „Czworościan GNSS” utworzony przez wektory łączące satelity i odbiorniki

Jeden z możliwych modeli (korzystam z [1]) wyznaczenia składowych wektora ∆AB na podstawie rejestrowa-

nych sygnałów satelitarnych GNSS przedstawia odległości ρ, na przykład satelita R – odbiornik A, w postaci różnicy

fazy sygnału emitowanego przez satelitę R i odbieranego przez odbiornik A i nazywa tę różnicę po prostu fazą Φ.

Uwzględniając podstawowe źródła błędów – niepewność wyznaczenia liczby N pełnych odłożeń fali λ na drodze od

R do A, wpływ atmosfery na tejże drodze, rozdzielony na wpływ jonosfery I i troposfery T, oraz wpływy błędów ze-

garów zarówno satelity δtS jak i odbiornika δtA, fazę Φ w chwili t1 przedstawia się zwykle w postaci:

Φ ( t ) = ρ ( t ) + N − δ t ( t ) + δ tR ( t ) + I R ( t ) + T R ( t ) (11) A

analogicznie faza Φ na drodze od satelity R do odbiornika B, rejestrowana w tej samej chwili t1, wyniesie:

Φ ( t ) = ρ ( t ) + N −

δ ( t ) +

t R

δ ( t ) + I R ( t ) + T R ( t ) . (12)

Wielkości N nie posiadają oznaczenia ti, gdyż w prawidłowo prowadzonej rejestracji sygnałów satelitarnych war-

tość N jest stała w czasie.

W obu powyższych wyrażeniach występuje błąd zegara satelity δtR . Różnica faz (11) i (12) będzie od niego

praktycznie uwolniona (pozostanie niewielka różnica wynikająca z faktu, że sygnały z satelity R zarejestrowane rów-

nocześnie przez dwa odbiorniki A i B, nie mogły być wyemitowane równocześnie – gdyż na ogół miały różnej dłu-

gości drogi do przebycia).

Odejmując stronami (11) od (12) otrzymamy równanie pojedynczej różnicy fazy:

Φ ( t )

= Φ ( t )

− Φ ( t ) . (13) AB

Proszę zwrócić uwagę na sposób oznaczania różnic za pomocą par wskaźników. Oczywiście zachodzi:

Φ ( t ) = ρ ( t ) + N −

δ ( t ) +

δ ( t ) + I R ( t ) + T R ( t ) (14)

Równanie pojedynczej różnicy (14), w którym różnicowaniu podlegają odczyty fazy sygnału nadchodzącego od

jednego satelity zarejestrowane symultanicznie przez dwa odbiorniki, wiąże szukane składowe wektora ∆AB z zareje-

strowanymi fazami. Zawarta w tym równaniu różnica odległości od satelity R do odbiorników A i B, oznaczana

ρ , to rzut wektora ∆

AB (10) na kierunek do satelity R, zadawany przez wektor jednostkowy (por. rys. 3):

→

eR ( t ) = ( eR ( t ), eR ( t ), eR ( t )) . (15) 1

Miarą długości tego rzutu jest iloczyn skalarny wektorów ∆AB i eR:

→

ρ ( t )

eR t . (16) AB

= ∆ AB ⋅ ( )

Podobnie otrzymamy równanie pojedynczej różnicy fazy dla satelity S:

Φ ( t ) = ρ ( t ) + N −

δ ( t ) +

δ ( t ) + I S ( t ) + T S ( t ) (17)

gdzie:

→

ρ ( t )

eS t . (18) AB

= ∆ AB ⋅ ( )

Tworząc równanie pojedynczej różnicy wyeliminowaliśmy wpływ resztowych błędów zegarów satelitów, pozo-

stały jednakże błędy zegarów odbiorników. Wyeliminujemy je tworząc równanie podwójnej różnicy fazy:

Φ ( t )

= Φ ( t )

− Φ ( t ) , czyli: (19)

Φ ( t )

= ρ ( t ) + N RS + I RS ( t ) + T RS ( t )

(20)

gdzie:

→

ρ ( t )

eS t

eR t

(20)

= ∆ AB ⋅ ( ( )

1 −

( ))

jest różnicą rzutów wektora ∆AB na kierunki do satelitów.

Równanie podwójnej różnicy fazy jest fundamentalnym równaniem służącym do precyzyjnego wyznaczenia

składowych wektora ∆AB w pomiarach techniką GNSS. Znajomość współrzędnych jednego z punktów końcowych

tego wektora oraz jego składowych, pozwala wyznaczyć współrzędne drugiego punktu z nawet subcentymetrową do-

kładnością. W równaniach podwójnych różnic fazy występują trzy wspólne niewiadome – składowe wektora ∆AB -

oraz właściwa każdej podwójnej różnicy niewiadoma liczba całkowita N. Ułożenie równań dla kolejnych epok t = t1,

t2, … i ich odjęcie stronami – otrzymamy w ten sposób równania potrójnych różnic fazy - pozwala wyeliminować

tę indywidualną niewiadomą. Do wyznaczenia pozostałych trzech niewiadomych będą wówczas potrzebne trzy rów-

nania potrójnych różnic, które można utworzyć posiadając zarejestrowane dane z czterech różnych satelitów – po-

dobnie jak w rozwiązaniu nawigacyjnym.

Ale o tym jak rozwiązać układ równań podwójnych różnic fazy i jakie inne możliwości niosą pomiary GNSS –

porozmawiamy na zajęciach.

Podstawowa wykorzystana literatura:

[1] Hofmann-Wellenhof B., Lichtenegger H., Wasle E.: GNSS - Global Navigation Satellite Systems. GPS,

GLONASS, Galileo, and more, Springer-Verlag Wien 2008, ISBN 978-3-211-73012-6