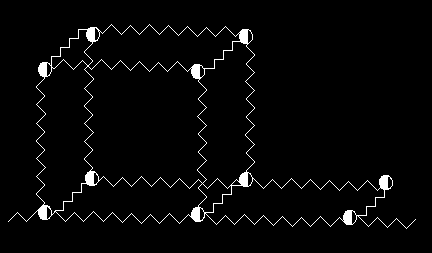Anna Linscheid

Zespół Fizyki, Akademia Rolnicza Do u ytku wewn trznego

WICZENIE 11

POMIAR WSPÓŁCZYNNIKA ROZSZERZALNO CI LINIOWEJ

CIAŁ STAŁYCH

Kraków, 02.2004

SPIS TRE CI

I. CZ

TEORETYCZNA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1. MIKROSKOPOWY OPIS ZJAWISKA ROZSZERZALNO CI LINIOWEJ...................................................................... 2

Mechaniczny model budowy sieci krystalicznej. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Oscylator harmoniczny w sieci krystalicznej. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Siły mi dzycz steczkowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

2. MAKROSKOPOWY OPIS ZJAWISKA ROZSZERZALNO CI LINIOWEJ .................................................................... 5

Izotropia i anizotropia. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Rozszerzalno liniowa ciał . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Rozszerzalno powierzchniowa i obj to ciowa ciał izotropowych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3. METODY POMIAROWE WSPÓŁCZYNNIKA ROZSZERZALNO CI CIEPLNEJ .......................................................... 7

II. CEL WICZENIA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

III. WYKONANIE WICZENIA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

IV. OPRACOWANIE WYNIKÓW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

V. LITERATURA UZUPEŁNIAJ CA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

ZAKRES WYMAGANYCH WIADOMOCI:

Poj cie temperatury, energii wewn trznej, ciepła. Mikroskopowy i makroskopowy opis

rozszerzalno ci cieplnej ciał. Rozszerzalno cieplna liniowa i obj to ciowa, termometry.

Sposoby przekazywania ciepła. Rola rozszerzalno ci cieplnej w powstawaniu pr dów

konwekcyjnych. Anomalna rozszerzalno wody i jej znaczenie

2

I. CZ

TEORETYCZNA

1. Mikroskopowy opis zjawiska rozszerzalno ci liniowej

Wymiary wi kszo ci ciał stałych wraz ze wzrostem temperatury ulegaj zmianie.

Ciepln rozszerzalno ci liniow ciała stałego nazywamy zmian jego wymiarów wywołan

zmian temperatury. Dla wyja nienia tego zjawiska posłu ymy si przedstawionym poni ej

modelem budowy ciała stałego.

Mechaniczny model budowy sieci krystalicznej

Ciała stałe maj budow krystaliczn lub bezpostaciow (amorficzn ). Kryształy

składaj si z atomów lub cz steczek rozmieszczonych w przestrzeni w sposób

uporz dkowany i tworz cych tzw. sie krystaliczn . Miejsca zajmowane przez poszczególne

atomy nazywaj si w złami sieci. Wzajemne odległo ci atomów s zbli one do ich

wymiarów i wynosz około 10-10m. Atomy wykonuj drgania wokół swoich poło e

równowagi. Amplitudy tych drga nie przewy szaj kilku procent wzajemnej odległo ci

atomów.

W niniejszym opracowaniu posłu ymy si mechanicznym modelem budowy sieci

krystalicznej. Według tego modelu wyobra amy sobie sie krystaliczn w postaci układu

cz steczek powi zanych ze sob spr ynkami (patrz rys.1), które obrazuj siły wzajemnego

oddziaływania s siednich atomów (siły spr ysto ci).

Oscylator harmoniczny w sieci krystalicznej

Atomy lub cz steczki gazu poruszaj si ruchem post powym, cz steczki ciała stałego

wykonuj drgania wokół poło e równowagi a rednia energia kinetyczna w obu przypadkach

ro nie wraz z temperatur . Wzrost energii wi e si ze wzrostem amplitudy drga .

Rys. 1. Model sieci krystalicznej

Rozwa my drganie pojedynczej cz steczki w sieci krystalicznej. Drgania odbywaj si

w trzech kierunkach ale dla jako ciowej oceny zjawiska wystarczy jednowymiarowa analiza

zachowania cz steczki. Zakładaj c, e działa na ni siła o warto ci proporcjonalnej do

wychylenia z poło enia równowagi, taki wprawiony w drgania układ nazywamy

jednowymiarowym oscylatorem harmonicznym a drgania te nazywamy harmonicznymi.

Wychylenie x cz steczki zmienia si wraz z upływem czasu zgodnie równaniem:

x = Asin(ωt+ϕ)

3

gdzie A - amplituda, czyli maksymalne wychylenie z poło enia równowagi, ω - cz sto , ϕ -

faza pocz tkowa. Zgodnie z prawami ruchu harmonicznego energia całkowita Ec drgaj cej

cz steczki o masie m, równa sumie energii kinetycznej Ek i potencjalnej Ep, jest niezale na od

czasu oraz poło enia cz steczki i proporcjonalna do kwadratu amplitudy:

2

mω 2A

Ec =

(1)

2

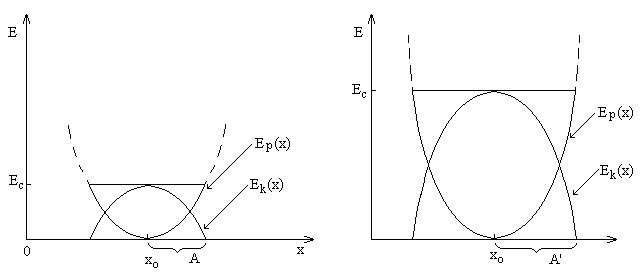
Rys. 2. Zale no energii całkowitej cz steczki od jej wychylenia z poło enia równowagi dla

modelu oscylatora harmonicznego

Na rys.2a, na osi pionowej zaznaczone s warto ci energii a na osi poziomej poło enia

x cz steczki w chwili t. x mo na traktowa jako odległo dwóch s siednich cz steczek ciała

stałego, z których jedna jest nieruchoma a druga podlega drganiom harmonicznym. Parabola

Ep przedstawia zale no energii potencjalnej od wychylenia (x-x0) z poło enia równowagi x0.

Parabola Ek przedstawia zale no energii kinetycznej od wychylenia (x-x0). Zgodnie z

równaniem (1) energia całkowita Ec=Ek+Ep cz steczki jest stała, Ec(x) =const, i na rys.2a

przedstawia j linia pozioma, któr nazywamy poziomem energetycznym. Gdy całkowita

energia drgaj cej cz steczki jest wi ksza, co przy tej samej cz sto ci drga oznacza

zwi kszenie amplitudy A, mówimy, e drgaj ca cz steczka znajduje si na wy szym poziomie

energetycznym. Tak sytuacj przedstawia rys.2b. Cz steczka oscyluje w wi kszych granicach

ni w przypadku przedstawionym na rys.2a ale poło enie rodka oscylacji pozostaje nadal

równe x0, a wi c rednia odległo pomi dzy cz steczkami jest taka sama.

Model oscylatora harmonicznego tłumaczy szereg wła ciwo ci sieci krystalicznej,

takich jak istnienie niezerowego ciepła wła ciwego, nie tłumaczy jednak zjawiska

rozszerzalno ci cieplnej stwierdzanej do wiadczalnie. Dla wyja nienia tego zjawiska nale y

zbada , czy siły działaj ce ze strony s siadów na pojedyncz cz steczk wychylon z

poło enia równowagi (siły mi dzycz syteczkowe) s rzeczywi cie proporcjonalne do warto ci

wychylenia i jakie s konsekwencje uwzgl dnienia w opisie sieci krystalicznej oddziaływa

nieharmonicznych.

Siły mi dzycz steczkowe

Rozszerzalno cieplna ciał stałych zwi zana jest z odmiennym ni w przybli eniu

harmonicznym charakterem zale no ci sił działaj cych pomi dzy s siednimi cz steczkami od

odległo ci pomi dzy nimi.

4

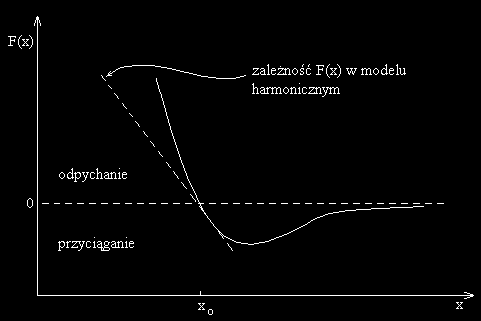
Rys. 3. Siła oddziaływania pomi dzy dwoma cz steczkami

w funkcji odległo ci pomi dzy nimi

Rys.3 przedstawia wykres przebiegu sił oddziaływania pomi dzy dwoma cz steczkami

w zale no ci od ich wzajemnej odległo ci x. Poniewa wykres nie jest lini prost (na rysunku

przedstawia j linia przerywana) taki model oddziaływania cz steczek nazwiemy "modelem

nieharmonicznym". Poło enie równowagi cz steczki x0 odpowiada odległo ci, dla której siły

odpychania i przyci gania równowa si . Gdy x>x0, przewa aj siły przyci gania (F<0, tzn.

zwrot siły przeciwny do zwrotu osi x), gdy x<x0, przewa aj siły odpychania (F>0).

Gdy zale no F(x) jest znana mo na znale zale no energii potencjalnej Ep

oddziaływania dwóch cz steczek od ich wzajemnej odległo ci i porówna j z przedstawion

na rys.2. T energi mo na obliczy posługuj c si nast puj cym wzorem:

x

Ep( )

x = − F( )

x ⋅ dx

∞

gdzie F(x) oznacza całkowit sił wzajemnego oddziaływania. Całk okre laj c Ep(x) mo na

tak e wyznaczy je li zale no F(x) znana jest jedynie w formie wykresu, takiego jak

przedstawiony na rys.3. Rys.4 przedstawia wynik całkowania. W przeciwie stwie do modelu

oscylatora harmonicznego krzywa przedstawiaj ca zale no Ep(x) nie jest symetryczna.

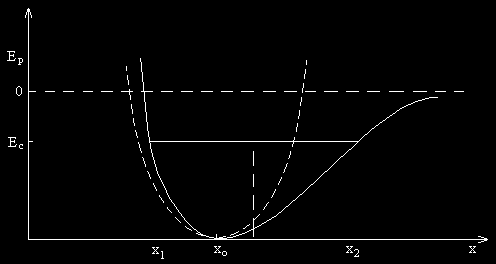
Rys. 4. Zale no Ep od odległo ci x w „modelu nieharmonicznym”

Tak jak w przybli eniu harmonicznym w "modelu nieharmonicznym" wraz ze

wzrostem temperatury energia całkowita cz steczek wzrasta i zajmuj one coraz to wy sze

poziomy energetyczne. Drgania cz steczek powoduj zmiany ich wzajemnych odległo ci w

przedziale od x1 do x2, Jak wida na rys.4, ze wzgl du na asymetri krzywej Ep(x), w wy szej

temperaturze rodek drga przesuwa si w prawo w stosunku do poło enia równowagi x0, co

5

odpowiada wzrostowi redniej odległo ci pomi dzy s siaduj cymi cz steczkami.

Powodowany zmian temperatury wzrost odległo ci s siednich cz steczek jest mały ale

zwielokrotniony przez liczb cz steczek wzdłu badanego kierunku daje obserwowaln

do wiadczalnie zmian wymiaru ciała.

2. Makroskopowy opis zjawiska rozszerzalno ci liniowej

Izotropia i anizotropia

Izotropi nazywamy niezale no wła ciwo ci fizycznych ciała od kierunku.

Anizotropi nazywamy brak izotropii.

Kryształy dzielimy na monokryształy i polikryształy. Polikryształy składaj si z du ej

liczby przypadkowo zorientowanych wzgl dem siebie małych kryształów, które tworz jedn

cało . Poniewa rozkład i orientacja tych małych kryształów jest dowolna, ciała

polikrystaliczne wykazuj izotropowo swoich wła ciwo ci. Ciała bezpostaciowe

(amorficzne), tzn. takie, które nie wykazuj prawidłowo ci w uło eniu cz steczek lub atomów,

tak e charakteryzuj si izotropowo ci .

Monokryształy to ciała krystaliczne, które w przeciwie stwie do polikryształów nie s

zlepkiem małych kryształów. Powstaj one z fazy ciekłej w procesie krystalizacji przez

dobudowywanie kolejnych warstw atomowych poczynaj c od jednego tzw. centrum

krystalizacji. Dla monokryształów rozszerzalno cieplna jest zjawiskiem anizotropowym i

pomiary rozszerzalno ci przeprowadza nale y dla ka dego z trzech kierunków osobno.

Konsekwencj anizotropii jest zmiana kształtu ciała przy zmianie temperatury.

Rozszerzalno liniowa ciał

Zale no ci długo ci ciał (l) od temperatury (t) s na ogół rosn ce. Malej ca zale no

l(t) jest wyj tkiem a jej przykładem mo e by rozszerzalno elaza w zakresie temperatur

750°C-780°C.

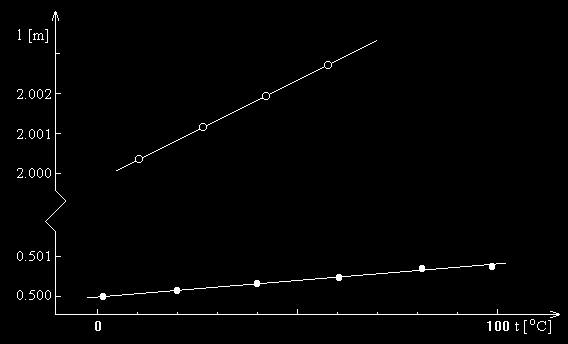
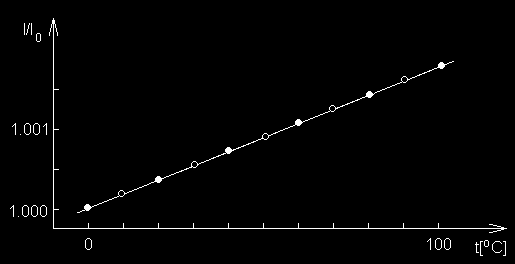
Rys. 5. Zale no długo ci (l) od temperatury (t) wyznaczona dla dwu ciał wykonanych z

mosi dzu o ró nych długo ciach pocz tkowych: l0 = 0.5 m i l’0 = 2 m

Na rys.5 przedstawiono typowe krzywe do wiadczalne zale no ci długo ci ciał od

temperatury wyznaczone dla ciał o ró nych długo ciach pocz tkowych wykonanych z tej

samej substancji (z mosi dzu). Jak wida przyrost długo ci ciała ∆l=lt-l0 zale y od przyrostu

6

temperatury i od tego jaka jest długo pocz tkowa (l0). Ponadto wida , e z du

dokładno ci zachodzi proporcjonalno ∆l~l0, tzn e ciało o czterokrotnie wi kszej długo ci

przy tej samej zmianie temperatury ∆t zwi ksza sw długo tak, e jej zmiana (∆l) jest tak e

czterokrotnie wi ksza. Liniowo wykresów wiadczy o proporcjonalno ci ∆l~∆t.

Podsumowuj c te obserwacje:

∆l ~ l0∆t

Je li chcemy zast pi znak proporcjonalno ci "~A" znakiem równo ci musimy

wprowadzi współczynnik proporcjonalno ci, który zale y od rodzaju substancji. Oznaczaj c go

przez α mo emy napisa :

∆l = α l0 ∆ t

Powy sza zale no prowadzi do definicji redniego współczynnika rozszerzalno ci

liniowej a. Jest on zdefiniowany nast puj co:

α = lt − l0

(2)

l0(t − t0)

gdzie: l0 jest długo ci ciała w temperaturze t0 natomiast lt długo ci w temperaturze t. Iloraz

(lt-l0)/l0 reprezentuje wzgl dn zmian długo ci. Definicj (2) odczyta mo na zatem w ten

sposób, e α jest "wzgl dn zmian długo ci ciała wywołan zmian jego temperatury o jeden

stopie " (Celsjusza lub Kelvina).

Z definicji (2) odczyta mo na jednostki, w których wyra ana jest warto a: 1/K (tzn.

K-1) lub 1/°C, gdzie K i °C oznaczaj odpowiednio stopnie Kelvina i Celsjusza. Niekiedy

stosuje si oznaczenie 1/deg (deg-1); deg jest mi dzynarodowym symbolem stopni.

Konsekwencj proporcjonalno ci zmiany długo ci ciała do jego długo ci pocz tkowej

jest to, e dwie krzywe rozszerzalno ci przedstawione na rys.5 dotycz ce wymiarów ró nych

ciał wykonanych z tej samej substancji mo na sprowadzi do jednej krzywej (rys.6)

wprowadzaj c na osi pionowej warto długo ci lt podzielonej przez długo pocz tkow l0.

Rys. 6. Zale no l/l0 od temperatury t wyznaczona dla ciał z rys. 5

Dokładniejsze pomiary wykazuj , e krzywe do wiadczalne przedstawione na rys.5 nie

s dokładnie prostymi. Ich kształt mo na opisa wielomianem drugiego lub trzeciego stopnia:

l

∗

2

t = l0(1+ α t

∆ + α ∆t + )

Tabela 1 przedstawia wyznaczone do wiadczalnie warto ci współczynników α i α* dla kilku

wybranych metali.

7

Tabela 1. Warto ci współczynników rozszerzalno ci liniowej wybranych substancji w

przedziale temperatur 10°C-90°C.

substancja

glin

mosi dz

ołów

elazo

α·105 [1/°C]

2.221

1.781

2.829

1.145

α*·108 [1/°C2]

1.14

0.98

1.20

0.71

Z danych zawartych w tabeli 1 wynika, e w przedziale od 10°C do 90°C warto składnika

α2∆t2 stanowi około 5% warto ci składnika α∆t. Zaniedbanie składników z wy szymi ni

pierwsza pot gami ∆t przy ilo ciowym opisie zjawiska rozszerzalno ci mo e by wi c

dopuszczalne. Nale y ponadto pami ta , e współczynniki α w definicji (2) i w powy szym

wielomianie nie s tymi samymi wielko ciami mimo tych samych oznacze . Dla odró nienia o

współczynniku a z definicji (2) mówimy jako o " rednim współczynniku rozszerzalno ci

liniowej".

Rozszerzalno powierzchniowa i obj to ciowa ciał izotropowych

Ciała izotropowe rozszerzaj c si nie zmieniaj swojego kształtu. Zmieniaj c wymiary

liniowe, zmieniaj pole powierzchni i obj to . Przez analogi do równania (2) definiujemy

współczynnik rozszerzalno ci powierzchniowej l:

λ = St − S0

(3)

S0(t − t0)

gdzie: S0 jest polem powierzchni ciała w temperaturze t0 (0°C) natomiast St polem w

temperaturze t. Stosuj c proste przekształcenia uzyskujemy zwi zek współczynnika

rozszerzalno ci powierzchniowej i liniowej: λ ≈ 2α

Analogicznie definiujemy współczynnik rozszerzalno ci obj to ciowej β:

β = Vt −V0

(4)

V0(t − t0)

gdzie: V0 jest obj to ci ciała w temperaturze t0 natomiast Vt obj to ci w temperaturze t.

Zwi zek współczynnika rozszerzalno ci obj to ciowej i liniowej jest nast puj cy:

β ≈ 3α

Podane powy ej zwi zki pomi dzy współczynnikami rozszerzalno ci powierzchniowej

i obj to ciowej a współczynnikiem rozszerzalno ci liniowej dobrze zgadzaj si z danymi

do wiadczalnymi dla ciał izotropowych.

Zmiany obj to ci ciał spowodowane zmianami temperatury powoduj zmiany ich

g sto ci. Poniewa masa m ciała nie ulega zmianie, zachodzi równo : Vt·ρt=V0·ρ0=m, gdzie

ρt oznacza g sto ciała w temperaturze t, ρ0 - g sto w temperaturze t0. Zatem:

ρ

ρ

=

0

1+ β (t − t0)

Zgodnie z powy sz zale no ci , gdy β>0 g sto ciała maleje wraz ze wzrostem temperatury.

3. Metody pomiarowe współczynnika rozszerzalno ci cieplnej

Pomiary warto ci współczynników rozszerzalno ci s przedmiotem działu fizyki

do wiadczalnej nazywanego dylatometri . Wyniki tych pomiarów s szeroko stosowane w

8

materiałoznawstwie w zagadnieniach, w których istotna jest znajomo zachodz cych wraz ze

zmianami temperatury zmian rozmiarów ciał i ich obj to ci. Najprostszy przyrz d do

mierzenia przyrostu długo ci - dylatometr przedstawiono na rys.7. Dokładno pomiaru

zmiany wymiarów ciała tym przyrz dem wynosi około 10µm. Istnieje szereg metod

pozwalaj cych zwi kszy t dokładno .

Dylatometry interferencyjne pozwalaj na pomiary o trzy rz dy wielko ci

dokładniejsze, tzn. s zdolne rejestrowa wydłu enia o warto ci ju około 0.01mm. Podobn

dokładno mo na uzyska w tzw. dylatometrze kwarcowym. W innej metodzie, zwanej

metod komparatora, pomiar zmiany długo ci wykonywany jest przy pomocy dwóch

mikroskopów.

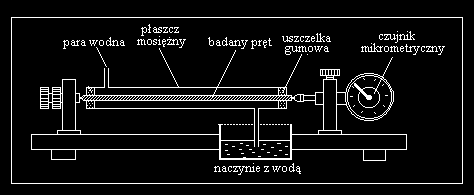
Rys. 7. Dylatometr - przyrz d do mierzenia współczynnika rozszerzalno ci cieplnej ciała

II. CEL WICZENIA

Celem wiczenia jest wyznaczenie współczynnika rozszerzalno ci liniowej dla

wybranych metali przy pomocy dylatometru.

III. WYKONANIE WICZENIA

Badane ciało ma posta pr ta umieszczonego wewn trz mosi nej rury, przez któr

przepuszcza si gor c par wodn (rys.7). Pomiary wykonujemy dla dwóch lub trzech kolejno

wybranych pr tów.

1. Przyjmujemy, e temperatura pocz tkowa pr ta t0 jest równa temperaturze

pokojowej, któr nale y odczyta na termometrze.

2. Zmierzy długo wybranego pr ta (l0) przy pomocy suwmiarki. Oszacowa

dokładno pomiaru długo ci.

3. Badany pr t umie ci w uchwycie, tak by ruchomy bolec czujnika

mikrometrycznego naciskał na płaski koniec pr ta. Nało y rurk gumow , przez

któr b dzie doprowadzana para wodna.

4. Tarcza podziałki mikrometru jest ruchoma. Obróci j tak, by zero skali pokrywało

si ze wskazówk mikrometru.

9

5. Wł czy ogrzewanie naczynia z wod i doprowadzi wod do wrzenia. Gdy woda

zacznie wrze nale y zmniejszy moc grzejn . Para skrapla si w naczyniu z zimn

wod .

6. Przepuszcza przez przyrz d par wodn tak długo, a wskazówka czujnika

mikrometrycznego wychyli si maksymalnie. Zanotowa wskazan przez czujnik

zmian długo ci pr ta ∆l. Skala czujnika mikrometrycznego posiada podziałk co

0.01mm a przyrz d zapewnia bł d systematyczny pomiaru nie przekraczaj cy

0.01mm.

7. Przyjmujemy, e temperatura ko cowa pr ta t jest równa temperaturze wrzenia

wody. Poniewa ta temperatura zale y od ci nienia powietrza, aktualne ci nienie

nale y odczyta na barometrze i zanotowa wynik pomiaru (pt0). Zgodnie ze

wskazówkami podanymi w broszurze "Opracowanie i prezentacja wyników

pomiarów", s.7-8, uwzgl dni poprawki ∆p1, ∆p2 i ∆p3 i zapisa skorygowan

warto ci nienia p. W tablicach znale temperatur wrzenia wody t.

8. Wyniki wpisa do tabeli wyników pomiarów pami taj c o identyfikacji materiału

pr ta (aluminium, mosi dz, elazo).

Tabela wyników pomiarów

rodzaj pr ta (metal)

l0 [mm] ∆l [mm] t0 [°C]

pt0 [kPa] p [kPa]

t [°C]

IV. OPRACOWANIE WYNIKÓW

1. Obliczy warto ci redniego współczynnika rozszerzalno ci liniowej a badanych

metali. Zgodnie z definicj (2) wynik mo e by wyra ony w [1/K] lub [1/°C], gdzie

K i °C oznaczaj odpowiednio stopnie Kelvina i Celsjusza.

Nale y zwróci uwag na to, e warto ró nicy temperatur t-t0 wyra ona w stopniach

Kelvina jest równa liczbowo warto ci wyra onej w stopniach Celsjusza, poniewa przej cie

do skali Kelvina polega na dodaniu 273 stopni zarówno do t jak i t0 a nie do ró nicy t-t0.

2. Uzyskane wyniki porówna z warto ciami tablicowymi podanymi w tabeli 1. Zasady

porównywania wyników z warto ciami tablicowymi podano w broszurze

"Opracowanie i prezentacja wyników pomiarów", s.26-27.

3. Obliczy maksymaln warto bł du ∆α współczynnika rozszerzalno ci a

wyznaczonego na podstawie wzoru (2) stosuj c metod ró niczki zupełnej lub

metod pochodnej logarytmicznej. Szczegółowe wskazówki na ten temat mo na

odnale w broszurze "Opracowanie i prezentacja wyników pomiarów", s.20-21, w

przykładach 8 i 9.

4. Wyniki ko cowe poda np. w formie nast puj cej tabeli:

metal

α [1/°C]

∆α [1/°C]

10

V. LITERATURA UZUPEŁNIAJ CA

Blinowski J., Trylski J., Fizyka dla kandydatów na wy sze uczelnie, Wydanie VIII. PWN,

Warszawa 1983

Bolton W., Zarys fizyki, PWN, Warszawa 1988

Buszmanow B.N., Chronow J.A., Wst p do fizyki ciała stałego, Warszawa 1973. s.98-100

Chyla K., Fizyka dla ZSZ, Wydanie trzecie, WSziP, Warszawa 1991. s.113-121

Dry ski T., Do wiadczenia pokazowe z fizyki, PWN, Warszawa 1964

Encyklopedia Fizyki, Tom 3, PWN, Warszawa 1974, s.249

Halliday D., Resnick R., Fizyka Tom 1, PWN, Warszawa 1975, s.641-647

Herman M., Kalesty ski A., Widomski L., Podstawy fizyki dla kandydatów na wy sze

uczelnie, PWN, Warszawa 1984, s.468

Gabrylewski E., Fizyka dla klasy I liceum ogólnokształc cego, technikum i liceum

zawodowego, PZWS, Warszawa 1973, s.217-224

Je ewski M., Kalisz J., Tablice wielko ci fizycznych oraz pomocnicze tablice matematyczne,

PWN, Warszawa 1957

Massalska M., Massalski J., Fizyka kl. IV dla liceum ogólnokształc cego, technikum i liceum

zawodowego, WSiP, Warszawa 1981, s.209-251

Szczeniowski S., Fizyka Do wiadczalna, Tom II, PWN, Warszawa 1976, s.15-26; 347-349

Wert Ch.A., Thompson R.M., Fizyka ciała stałego, PWN, Warszawa 1974. s.40