Badania operacyjne Wykład 6

Zagadnienie przydziału

Plan wykładu

 Zagadnienie przydziału

 Algorytm węgierski

2013-12-13

2

Zagadnienie przydziału

 Optymalna alokacja szeroko pojętych zasobów

 Kryt

i

er

i

am l

a k

o

j

ac iji j t

es

j

na cz ś

ę i

c j

e :



Minimalizacja kosztów lub czasu wykonywania planowanych zadań,



Maksymalizacja efektów p racy

pracy (np.

ilo

ść

ilo wyprodukowanych

wyrobów).

2013-12-13

3

Zagadnienie przydziału

 Najogólniej problem można sformułować następująco:



N wyrobów (czynności) m oż

mo na wykona

ć na P miejscach produkcji (w zakładach, na stanowiskach pracy, maszynach)



Znane są ograniczone moce prod k u cyjne poszczegól

ólnych i

m j

e sc

pracy (np. dopuszczalny czas pracy), a często także zadania planowe w zakresie produkcji wyrobów



Podana jest macierz, w której znajdują się koszty (czas pracy lub wydajność) na danym miejscu prac p

y prz

p y wykonywaniu

odpowiedniego zadania.

2013-12-13

4

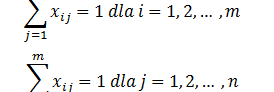
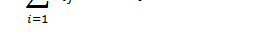
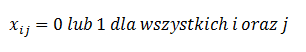
Zagadnienie przydziału

 Szczególnym przypadkiem zadań alokacyjnych jest zagadnienie przydziału z dodatkowymi ograniczeniami, ż k

e ż

a da czynność

ż

mo e być

k

wy onana tylk

lk

i

o raz ż

e na

każdym stanowisku można wykonać tylko jedną czynność w z

ak

zakładanym przedziale

przedziale czasu.

2013-12-13

5

Zagadnienie przydziału

 Model matematyczny zagadnienia przydziału z ograniczeniami, że każdą czynność można wykonać tylk

lko raz i ż

e na k ż

a d

t

ym s anowi k

s

ż

u mo na wyk

ć

ona tylk

lko

jedną czynność, jest następujący:



Funkcja celu (np. minimalizacja czasu pracy):



Ograniczenia:



Warunki brzegowe:

2013-12-13

6

Zagadnienie przydziału

 Zagadnienie przydziału można rozwiązać:



Metodami programowania liniowego



Metodami programowania całkowitoliczbowego



Specjalnie opracowanymi do tego celu algorytmami (np algorytmem

.

w

ę

w gierskim

ę

).

2013-12-13

7

Algorytm węgierski (min)

 Krok 1: Przekształcenie macierzy kosztów tak, aby w każdym jej wierszu i w każdej kolumnie występowało co j

na

i

mn ej j d

e no zero.

W tym celu należy znaleźć minimalny element w każdym wierszu macierzy, odjąć go od każ ka dego elementu

elementu danego

wiersza i zbudować nową macierz.

Jeś

Je li

ś trzeba (gdy nie ma

ma w ka

ż

ka dej

ż

kolumnie zera) t

, o

to

z każdego elementu kolumny należy odjąć jej najmniejszy element i zbudować nową macierz.

ą

2013-12-13

8

Algorytm węgierski (min)

 Krok 2: Skreślenie – w przekształconej macierzy kosztów

– wszystkich wierszy i kolumn zawierających zera, przy ż

u

i

yc

ż

u mo liwi

j

e na

i

mn ejszej lili b

cz y li ii

n

i

poz

h

omyc

i pionowych (należy pokryć liniami wszystkie zera w całej macierzy).

Jeśli najmniejsza liczba linii niezbędnych do pokrycia wszystkich zer

j est

jest r

ówna

równa wymiarowi macierzy,

macierzy, to

mo

ż

mo liwe

jest otrzymanie rozwiązania optymalnego. Przejść do kroku 4.

Jeśli liczba skreśleń jest mniejsza od wymiaru macierzy, należy przejść do kroku 3.

2013-12-13

9

Algorytm węgierski (min)

 Krok 3: Jeśli liczba skreśleń jest mniejsza od wymiaru macierzy, to należy znaleźć najmniejszy nieskreślony l

e

t

emen i:



Odjąć go od elementów nieskreślonych



Dodać

Doda go do elementów

podwójnie skreś

skre lonych

Elementy skreślone jedną linią (raz) zostawiamy bez zmian!

Przejść do kroku 2.

2013-12-13

10

Algorytm węgierski (min)

 Krok 4: Ustalenie rozwiązania optymalnego w macierzy końcowej, polegającego na takiej konstrukcji nowej maci

b

erzy, a y j d

e

ki

yn

l

zna azł

i

y s ę tylk

lk

l

o w po ach z

i

zeram

(przy czym należy pamiętać, aby w każdym wierszu i w

k

aż

ka dej kolumnie wystą

wyst pi

ą ła tylko

tylko jedna

jedynka).

Często możliwe jest uzyskanie kilku rozwiązań optymalnych, dających

ą

tę

t sam

ą

sam wartość

warto funkcji celu.

celu.

2013-12-13

11

Algorytm węgierski (max)

 Aby rozwiązać problem maksymalizacji zagadnienia, należy:



Pomnożyć macierz (każdy element macierzy przez -1)



Następnie rozwiązać problem analogicznie jak problem minimalizacji.

2013-12-13

12

Literatura

 Ignasiak E. (red.), Badania operacyjne. Polskie Wydawnictwo Ekonomiczne, Warszawa 1996.

 Mitchell G.H. (red.), Badania operacyjne. Metody i przykłady. Wydawnictwo Naukowo-Techniczne, Warszawa 1977

.

 Łucki Z. (red.), Matematyczne techniki zarządzania.

Przykł

Przyk ady i zadania

zadania. Wydawnictwa

Wydawnictwa AGH K

, raków

Kraków 1998

.

 Sawik T., Badania operacyjne dla inżynierów zarządzania

ą

. Wydawnictwa AGH K

, raków

Kraków 1998

.

 Wagner H.M., Badania operacyjne: zastosowania w zarządzaniu. Pa

ą

ństwowe Wydawnictwo Ekonomiczne, , Warszawa 1980.

2013-12-13

13