Zarządzanie i Marketing

II rok

BADANIA OPERACYJNE - wykłady

dr hab. Marek Miszczyński

Wykład I

14.II.2003

Tematyka przedmiotu:

1. Badania operacyjne w procesie podejmowania decyzji gospodarczych.

2. Podejmowanie decyzji w warunkach pewności. Liniowe modele decyzyjne - budowa i rozwiązywanie (metoda simplex, zagadnienie wycen dualnych i elementarna analiza postoptymalizacyjna).

3. Optymalizacja w zagadnieniach przewozowych. Klasyczne kosztowe zagadnienie transportowe oraz zagadnienia transportowe z kryterium czasu. Zagadnienia pochodne - zagadnienie optymalnego przydziału.

4. Wybrane nieliniowe problemy decyzyjne rozwiązywalne metodami dla zagadnień liniowych. Poszukiwanie optymalnej decyzji o najlepszym wskaźniku efektywności (modele decyzyjne z ilorazową funkcją celu). Poszukiwanie decyzji najlepiej przybliżającej do zadanych przez decydenta celów (model programowania celowego).

5. Podejmowanie decyzji w warunkach niepewności i ryzyka - pojęcia podstawowe, podstawowe kryteria wyboru decyzji, gry z „naturą”, analiza drzew decyzyjnych w procesie podejmowania decyzji. Rola dodatkowej informacji w procesie decyzyjnym (analiza bayesowska).

6. Modelowanie złożonych przedsięwzięć wieloczynnościowych (zarządzanie projektami). Podstawowe metody w zarządzaniu projektami:

• Deterministyczna analiza przedsięwzięcia (metoda CPM).

• Stochastyczna analiza przedsięwzięcia (metoda PERT).

• Kosztowo - czasowa analiza przedsięwzięcia (metoda LESS).

7. Modelowanie procesów o charakterze masowym (elementy teorii masowej obsługi) - pojęcia podstawowe, klasyfikacja systemów masowej obsługi. Przykłady zastosowań wybranych modeli M/M/k w zarządzaniu.

Wstęp:

Różnie się kojarzy problem badań operacyjnych. Początki badań operacyjnych to II Wojna Światowa i to jest próba zastosowania tej metodologii do minimalizacji strat w konwojach atlantyckich, stąd też przylgnęła nazwa operation(s) research do tego przedmioty, do tych grup metod. Nazwa ta została ukuta przez amerykanów w latach pięćdziesiątych, a już po około dziesięciu latach zmienili generalnie jej nazwę na management science, czyli naukowe zarządzanie. Tej nazwy amerykanie używają do dziś.

Definicji przedmiotu jest bardzo wiele. Najtrafniejszą chyba podał H. Wagner, który o tej dyscyplinie wyraził się w ten sposób: Jest to zastosowanie metod matematyczno - statystycznych do wspomagania decyzji gospodarczych.

Klasyfikacja procesów decyzyjnych:

Jeśli sytuacja decyzyjna jest taka, że jednej decyzji odpowiada z prawdopodobieństwem równym 1 tylko jeden wynik, to mówimy, że podejmujemy decyzję w warunkach pewności.

D ^{p = 1} W

Mogłoby się to wydawać bardzo proste. Problem jednak pojawia się wtedy, kiedy takich decyzji jest nieskończenie wiele, albo na tyle dużo, że przepatrzenie wszystkich wariantów jest praktycznie niemożliwe. Oczekujemy na ogół, że mając proces decyzyjny, to wynik tej decyzji chcemy poznać w rozsądnym czasie.

Jeśli mamy decyzję, a wyniki mogą być różne, czyli jednej decyzji odpowiada więcej, niż jeden wynik, to jest drugi biegun.

W₁

D W₂

...

W_n

Mamy do czynienia z wynikiem, który jest zmienną losową i w zależności od tego, jakie informacje posiadamy o tej zmiennej losowej, to są 3 przypadki:

1. Jeśli wiemy tylko tyle, że jednej decyzji odpowiada więcej, niż jeden wynik, który jest zmienną losową i poza tym nie mamy żadnych danych o tej zmiennej, to mówimy o podejmowaniu decyzji w warunkach niepewności. Jeśli nie znamy rozkładu prawdopodobieństwa zmiennej losowej W, to podejmujemy decyzję w warunkach niepewności.

2. Jeśli znamy rozkład prawdopodobieństwa zmiennej losowej W, lub jej funkcję gęstości, to mówimy o podejmowaniu decyzji w warunkach ryzyka.

3. Jeżeli nie znamy rozkładu zmiennej, ale znamy niektóre momenty rozkłady, jak np. średnia, odchylenie, kwartyle, czy modalną, wówczas jest to podejmowanie decyzji w warunkach niepełnej informacji.

Podejmowanie decyzji w warunkach pewności:

Liniowe modele decyzyjne:

Twierdzenie Weierstrassa:

Funkcja liniowa osiąga swoją wartość największą, bądź najmniejszą w zbiorze wypukłym nie wewnątrz tego zbioru, ale na jego brzegach. Jeśli ten zbiór wypukły jest to wielobok wypukły (inaczej wielościenny obszar wypukły), to w konkretnych punktach brzegowych, czyli w wierzchołkach tego zbioru.

Każdemu takiemu punktowi wierzchołkowemu odpowiada w przestrzeni odpowiednio większej tzw. rozwiązanie bazowe układu równań.

Struktura liniowego modelu decyzyjnego:

Każdy model decyzyjny, w tym i liniowy składa się z następujących elementów:

1. Funkcji celu, nazywanej funkcją kryterialną. Na ogół jest to funkcja bardzo wielu zmiennych.

f(x) = f(x₁, x₂, ... , x_n)

2. Ograniczeń, które prowadzą do tzw. zbioru decyzji dopuszczalnych.

Problem sprowadza się do znalezienia wartości największej, bądź najmniejszej funkcji celu, przy warunku, że zmienna x należy do zbioru decyzji dopuszczalnych X , co zapisujemy następująco:

f(x) → max

(min)

x ∈ X

To jest struktura modelu decyzyjnego.

Zapis powyższy może kojarzyć się ze znajdowaniem ekstremów lokalnych, ale chodzi tu o znajdowanie największych, bądź najmniejszych wartości ze zbioru decyzji dopuszczalnych. Różnicę można pokazać na poniższym rysunku:

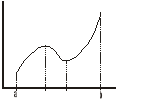
Dana jest taka funkcja określona na przedziale <a, b>. Chodzi nam o wartości x = a lub x = b, w zależności od tego, czy chodzi nam o wartość największą, czy najmniejszą. Ekstrema lokalne znajdują się gdzie indziej. Przyjęte jest, że pisząc max, bądź min mamy na myśli, w sensie zapisu matematycznego, bądź supremum, bądź infinium:

f(x) → sup

(inf)

Oczywiście, w przypadku liniowych modeli decyzyjnych jest to obojętne i ten problem nie wystąpi, bo funkcja nie ma ekstremów lokalnych.

Decyzja optymalna musi mieć tą cechę, że musi należeć do zbioru decyzji dopuszczalnych, czyli nie ma mowy o tym, żeby mówić, że mamy do czynienia z decyzją optymalną, jeśli to nie jest decyzja dopuszczalna. Jest to decyzja, dla której funkcja f(x) osiąga swoją wartość największą, bądź najmniejszą. Decyzję optymalną oznaczamy jako x^O ∈ X.

Wykład II

21.II.2003

Przy metodzie simplex model decyzyjny należy doprowadzić do postaci kanonicznej. W tym celu każdą z nierówności przekształcamy w odpowiednie równanie. W równaniu tym dokładamy bądź zmienne swobodne (ang. slack variables), kiedy nierówność jest postaci mniejsze lub równe, bądź też nadwyżki (ang. surplus) dopisywane z minusem, kiedy nierówność jest postaci większe lub równe. Jeśli mamy do czynienia z każdą inną relacją, niż mniejsze lub równe, to zawsze pojawi się zmienna sztuczna, pomocnicza.

Matematycy formułują ograniczenie dla zmiennej sztucznej t jako żądanie, że t = 0, bo wiadomo, że problem ma rozwiązanie i w związku z tym zrób tak, żeby znaleźć rozwiązanie problemu, ale ekonomiści nie mają pojęcia, czy zbudowany przez nich model ma w ogóle jakiekolwiek rozwiązanie i dla tego na wszelki wypadek formułują to jako żądanie, że zmienna sztuczna ma przyjmować wartości nieujemne. W zależności od tego, jak w rozwiązaniu optymalnym zachowa się zmienna sztuczna t, wiemy czy problem jest sprzeczny, czy nie.

t ≥ 0

Jeśli zbudujemy postać kanoniczną modelu decyzyjnego, to zadanie polega na przepatrzeniu rozwiązań bazowych i wybraniu takiego, dla którego wartość funkcji celu będzie największa. Ogólnie, jeśli mamy m ograniczeń i n zmiennych, to maksymalna liczba iteracji, czyli liczba przepatrzonych rozwiązań bazowych nie powinna przekraczać 3/2 m. To rozwiązuje się w tabelach simpleksowych.

Zmienne swobodne określają niewykorzystane zasoby, natomiast nadwyżki określają, jak sama nazwa wskazuje, nadwyżki zasobów nad dany rozmiar.

Kiedy mamy już rozwiązanie optymalne, kluczem do wszelkich dalszych obliczeń jest znajomość macierzy odwrotnej do macierzy bazy, w tym przypadku do bazy optymalnej.

B_o^-1 = ?

Można oczywiście odwrócić macierz, ale w tabeli simplex wszystkie dane już się znajdują, trzeba je tylko znaleźć. Tam, gdzie na początku procesu obliczeniowego była macierz jednostkowa, tam po każdej iteracji znajduje się macierz odwrotna do macierzy aktualnego rozwiązania bazowego.

Zadania i wyceny dualne:

Często jest tak, że ktoś, kto wykorzystuje taki model uważa, że tyle się napracował przy rozwiązaniu, że sprawę ma już załatwioną. Nic z tych rzeczy. W praktyce zastosowanie takich modeli do wspomagania procesów decyzyjnych to jest prawie niekończący się proces:

1. zbuduj model,

2. rozwiąż go,

3. przeanalizuj rozwiązanie.

Na ogół decydentom nie podoba się wiele rzeczy w tym modelu. Przypominają sobie wiele rzeczy, których nie zasugerowali budowniczemu modelu i w związku z tym brak takich informacji rzutuje na model. W związku z tym trzeba poprawić taki model, jeszcze raz go rozwiązać, poprawić,itd. i ten proces weryfikacja - rozwiązanie trwa. W pewnym momencie następuje konsensus - decydent mówi, że uzgodnił już wszystkie elementy modelu, a zatem to rozwiązanie może mieć już walor praktyczny.

Nawet dla superszybkich komputerów rozwiązanie takiego modelu nie jest sprawą szybką. W związku z tym trzeba się zastanowić, czym dysponujemy, żeby zadowolić takiego decydenta. Jedno z pierwszych pytań, jakie nasuwają się decydentami brzmi tak: „Co by było, gdybym miał o 1 minutę czasu pracy więcej, albo o 1 kg więcej surowca itd.”. Można zmienić te wartości i rozwiązać model od nowa, ale jest to zbyt wolne. Z każdym ograniczeniem związana jest pewna niewiadoma, zwana wyceną dualną (ang. shadow price). Wycena dualna informuje właśnie o ile wzrośnie optymalna wartość funkcji celu, jeśli zwiększymy, bądź zmniejszymy któreś z ograniczeń (odpowiadające danej wycenie dualnej) o jednostkę. Matematycznie można to zapisać następująco:

Jest to krańcowy przyrost wartości funkcji celu w do krańcowego przyrostu zasobu b_i. Ten zapis niezbyt nadaje się do praktycznej interpretacji i w związku z tym te delty greckie zastępujemy przyrostami, przy założeniu, że Δb_i = 1:

Uznajemy, że jedynka jest tym epsilonowym otoczeniem danego punktu i tutaj błędu nie będzie. Jest to taka różnica jak między przyrostem funkcji a różniczką. Przy odpowiednio dużej skali wyjdzie na to samo czy użyjemy ε, czy jedynki. Chodzi o wartość użytkową tej informacji. Wyceny dualne będziemy interpretowali jako przyrost optymalnej wartości funkcji celu na skutek przyrostu wyrazu wolnego danego ograniczenia o jednostkę. W takim razie potrafimy odpowiedzieć na dość trudne pytanie bez rozwiązywania modelu od początku.

Tw.:

Jeśli wyjściowe zadanie posiada skończone rozwiązanie optymalne, to drugie z zadań, czyli zadanie dualne (którego zmiennymi są wyceny dualne) również posiada skończone rozwiązanie optymalne. Wartości optymalne funkcji celu obu zadań są sobie równe. Jeżeli zadanie wyjściowe jest sprzeczne, to drugie z zadań nie posiada skończonego rozwiązania optymalnego. Twierdzenie odwrotne nie jest prawdziwe.

Aby uzyskać wyceny dualne, nie trzeba wcale budować modelu dualnego. Rozwiązując zadanie wyjściowe, po drodze niejako zdobywamy informacje o wycenach dualnych.

Tw. o rozwiązaniu zadania dualnego:

Jeżeli wyjściowy problem decyzyjny posiada swoje obliczone rozwiązanie optymalne, to również posiada skończone rozwiązanie optymalne model dualny, a rozwiązanie to wylicza się ze wzoru:

Ten wzór bezwzględnie wymaga znajomości macierzy B.

Należy uważać na miana wycen dualnych. Każde miano jest ilorazem miana funkcji celu zadania dualnego, przez miano danego zasobu.

Dobrze jest zapisać sobie dla każdego ograniczenia wartość optymalną jeśli chodzi o zmienne swobodne, oraz o wyceny dualne. Zawsze jest tak, że przynajmniej jedna z tych zmiennych jest równa zero. Nie może być tak, że obydwie te zmienne mają wartość niezerową. W matematyce, żeby osiągnąć takie żądanie, zapisalibyśmy:

Może zdarzyć się tak, że jedna, jak i druga zmienna będą miały wartość zerową.

Jeśli mamy niewykorzystane zasoby, to trudno oczekiwać, że ich zwiększenie spowoduje zwiększenie wartości funkcji celu.

Analiza wrażliwości:

Powstaje natychmiast kolejne pytanie - Jak długo ta informacja jest prawdziwa? Jest ona prawdziwa w pewnym epsilonowym otoczeniu. Myśmy zrobili z tego otoczenie jednostkowe - jest sferą o promieniu 1. W praktyce informacja ta może pozostawać prawdziwa dla większych przedziałów. Informacja, która odpowie na pytanie, jak długo informacja o wycenach dualnych jest prawdziwa będzie się kryła w tzw. analizie wrażliwości (ang. sensitivity analisys).

Należy odpowiedzieć na pytanie o ile można zmniejszyć lub zwiększyć wartość danego zasobu (oznaczoną przez b_i), aby informacja o wycenach dualnych była prawdziwa. W tym celu należy znaleźć rozwiązanie bazowe. Żeby obliczyć wektor wartosci zmiennych bazowych, to trzeba macierz odwrotną do macierzy bazy pomnożyć przez wektor wyrazów wolnych układu równań:

Należy przypomnieć tu żądania brzegowe: wszystkie x-y i s-y mają być nieujemne. Wartości zmiennych niebazowych mają być nieujemne:

Podstawiając pod powyższy warunek dane, z pominięciem szukanej wartości b_i można dojść do układu nierówności z 1 niewiadomą, po rozwiązaniu których otrzymujemy szukany przedział. Każdy taki przedział powstaje przy założeniu, że pozostałe parametry modelu nie ulegają zmianie. Nie wolno dokonywać zmian w więcej, niż jednym parametrze. Każdy z przedziałów uzyskanych w analizie wrażliwości jest prawdziwy, że tylko ten parametr ulegnie zmianie, a wszystkie inne pozostaną bez zmian. Można poprawiać kilka parametrów po kolei, ale nigdy jednocześnie.

Nasz model składa się nie tylko z wyrazów wolnych ograniczeń, ale również z funkcji celu. Może powstawać kolejne pytanie: W jakim przedziale mógłbym przekalkulowywać jeden ze współczynników funkcji celu, żeby aktualna decyzja nie podlegała zmianie? Identyczne przedziały są również wyliczane na podstawie analizy wskaźników optymalności dla współczynników funkcji celu. To jest pewien kanon, jeśli chodzi o analizę wrażliwości w liniowych modelach decyzyjnych.

Wykład III

28.II.2003

Jeżeli przedział otrzymany w wyniku analizy wrażliwości z jakichś powodów nie pokrywa rozwiązania optymalnego, to oznacza, że gdzieś pojawił się błąd. Najczęściej jest to błąd rachunkowy. W każdym razie przedział ten zawsze musi pokrywać oryginalną wartość parametru. Przedział analizy wrażliwości powstaje przy założeniu, że wszystkie parametry, oprócz danego są stałe - takie, jak w oryginale. Zawsze można dokonać zmiany tylko w obrębie jednego przedziału.

Również współczynniki funkcji celu mają podobne przedziały. Aby wyjaśnić jak one powstają, należy odwołać się do tablicy simplex. Współczynniki funkcji celu są odpowiedzialne m. in. za wartości wskaźników optymalności. Każda zmiana w tych współczynnikach odbija się natychmiast na zmiany w wektorze c^B. Aby obliczyć analizę wrażliwości dla współczynników funkcji celu, należy pod jeden z nich podstawić zmienną i obliczyć stosowne nierówności.

Przy zmianach tych współczynników zmienia się kierunek gradientu. Nie oznacza to tego, że przy zmianie czy współczynników funkcji celu, czy wyrazów wolnych decyzja pozostanie taka sama. Rozwiązanie optymalne się wtedy zmieni, ale wciąż będzie wyznaczane przez przecięcie tych samych prostych (ograniczeń), czyli będzie to jakby ten sam wierzchołek, jednak już o innym położeniu. Charakter decyzji nie zmieni się. Przy zmianach parametru w granicach zbioru określonego przy analizie wrażliwości, skład rozwiązania bazowego pozostanie taki sam.

Po takiej analizie można zrobić syntetyczne zestawienie w formie tabeli, która zestawia rozwiązanie i wszystkie możliwe przedziały wrażliwości.

Nieliniowe modele decyzyjne:

Będziemy poszukiwali takiej decyzji, przy której nie tyle wolumen, ale przy której stosunek pewnych wielkości będzie największy, bądź najmniejszy. Będziemy tutaj mieć na myśli wszelkie wskaźniki ekonomiczne, które wyrażają się stosunkiem.

Nieliniowy model decyzyjny I:

Dla przykładu w liczniku znajdzie się wartość produkcji w cenach zbytu, a w mianowniku będzie zużyty czas pracy maszyn. Będzie to produktywność maszyn. Tym lepiej będzie, im ten wskaźnik będzie jak największy. W tym przypadku będziemy mieli do czynienia z funkcją celu, która już nie będzie liniowa. W sensie matematycznym będzie to hiperbola w przestrzeni R³. Modele te są dużo częściej wykorzystywane, niż modele liniowe.

(maszyny) x₁ + 2x₂ ≤ 500

(surowiec) x₁ + x₂ ≤ 350

(min. zysk) 2x₁ + x₂ ≥ 600

(war. brzegowe) x₁ ≥ 0, x₂ ≥ 0

Model zastępczy będzie modelem liniowym, który da się rozwiązać metodą simplex. Zamiast zmiennych x₁, x₂ pojawią się zmienne u₁, u₂, oraz zmienna u₀ będąca definicją mianownika. Jako funkcję celu przyjmujemy funkcję licznikową:

Nową zmienną u₀ przywiązujemy w ograniczeniach do wyrazu wolnego i przenosimy na lewą stronę, relację pozostawiając bez zmian:

(maszyny) u₁ + 2u₂ - 500u₀ ≤ 0

(surowiec) u₁ + u₂ - 350u₀ ≤ 0

(min. zysk) 2u₁ + u₂ - 600u₀ ≥ 0

Potrzebne jest jeszcze jedno ograniczenie, które w sposób pośredni będzie definiowało nam mianownik:

(mianownik) u₁ + 2u₂ + 0u₀ = 1

(war. brzegowe) u₁ ≥ 0, u₂ ≥ 0 u₀ > 0

Ograniczenie u₀ jako mianownik nie może być równe zeru, więc konieczny jest warunek u₀ > 0. Ostra nierówność w tym warunku odcina nas od brzegu zbioru, co nie pozwala na użycie twierdzenia Weierstrassa, a więc nie można użyć metody simplex. Praktyka rozwiązania jest taka, że zamiast tego ograniczenia przyjmujemy miękkie ograniczenie u₀ ≥ 0 i pojawia się model liniowy. Po rozwiązaniu tego modelu mogą pojawić się dwie sytuacje:

1. Jeżeli w rozwiązaniu optymalnym wartość zmiennej u₀^O byłaby równa zeru, to model wyjściowy byłby sprzeczny.

2. Druga możliwość występuje najczęściej i wtedy optymalna wartość u₀^O jest większa od zera i wtedy wyjściowy model ma rozwiązanie.

Po zastosowaniu metody simplex otrzymujemy:

Przekształcenie rozwiązania modelu zastępczego na rozwiązanie modelu wyjściowego jest bardzo proste. Wartości zmiennych decyzyjnych uzyskujemy dzieląc określone u związane ze zmienną decyzyjną przez wartość u₀^O. Jeśli istnieje rozwiązanie modelu zastępczego, to optymalne wartości funkcji celu g, oraz h są sobie równe:

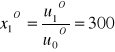
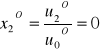
Nieliniowy model decyzyjny II - model programowania celowego:

Ten model decyzyjny nazywany jest wprost goal programming. Tutaj będzie chodziło o znalezienie takiego rozwiązania, które umożliwi minimalizację odchyleń od zadanych celów. Cele można stawiać sobie różne, np.:

Cel 1: Osiągnąć wartosć produkcji 1000 $.

Cel 2: Osiągnąć zysk 800 $

Może tu występować dowolna, byle skończona liczba takich celów.

Można powiedzieć, że wszystkie cele są równe, ale niektóre są równiejsze. Można więc zdywersyfikować te cele. Dla każdego celu należy przyjąć odpowiednią wagę:

w_k ∈ (0, 1>

Im cel jest ważniejszy, tym dostaje wagę bliżej jedności, a im jest mniej ważny bliżej zera.

Dla naszego przykładu przyjmijmy:

k = 1, 2

w₁ = 0,4

w₂ = 0,8

Zadanie będzie polegało na takim dobraniu wartości zmiennych x₁ i x₂, żeby znaleźć się jak najbliżej zadanych celów. Może tutaj występować nadszacowanie, lub niedoszacowanie.

Funkcja celu wygląda następująco:

(maszyny) x₁ + 2x₂ ≤ 500

(surowiec) x₁ + x₂ ≤ 350

(min. zysk) 2x₁ + x₂ ≥ 600

(war. brzegowe) x₁ ≥ 0, x₂ ≥ 0

Nie można użyć metody simplex, ze względu na nieliniowość. Ujęcie w wartość bezwzględną, mimo formy liniowej, nie można mówić o funkcjach liniowych, a więc funkcja celu nie jest funkcją liniową.

Model zastępczy:

Należy na początek wprowadzić następujące oznaczenia:

s₁⁺ (s₁^-) - nadszacowanie (niedoszacowanie) celu pierwszego.

s₂⁺ (s₂^-) - nadszacowanie (niedoszacowanie) celu drugiego.

Takich definicji musi być tyle, ile jest celów. Te zmienne są inną definicją tego, co znajduje się pod znakiem wartości bezwzględnej. Są to albo nadwyżki ponad określoną wartość celu, bądź niedobory poniżej tej wartości. Te zmienne zmieniają bardzo szybko funkcję celu:

(maszyny) x₁ + 2x₂ ≤ 500

(surowiec) x₁ + x₂ ≤ 350

(min. zysk) 2x₁ + x₂ ≥ 600

Pojawi się teraz tyle dodatkowych ograniczeń, ile jest celów. Będą one stanowić jakby definicje zmiennych s₁⁺, s₁^-, s₂⁺, s₂^-:

(cel 1) 3x₁ + 4x₂ - s₁⁺ + s₁^- = 1000

(cel 2) 2x₁ + x₂ - s₂⁺ + s₂^- = 800

(war. brzegowe) x₁ ≥ 0, x₂ ≥ 0, s₁⁺ ≥ 0, s₁^- ≥ 0, s₂⁺ ≥ 0, s₂^- ≥ 0

Przy konkretnych wartościach x₁ i x₂ niemożliwe jest jednoczesne niedoszacowanie i nadszacowanie. Trzeba się przed tym zabezpieczyć, wprowadzając taką „blokadę nonsensu”:

(„blokada nonsensu”) s₁⁺⋅s₁^- = 0, s₂⁺⋅s₂^- = 0

Mamy tutaj gwarancję, ze przynajmniej jedna z tych zmiennych będzie równa zeru. Takich ograniczeń nie da się jednak wprowadzić. Można to jednak ominąć.

Macierz bazowa jest to taka macierz kwadratowa, która jest macierzą nieosobliwą, czyli daje się odwrócić. Na to, aby macierz taka była nieosobliwa, to nie może zawierać wierszy, lub kolumn współliniowych, czyli takich, że dany wiersz lub daną kolumnę da się przedstawić jako liniową kombinację pozostałych. Jeśli tak, to macierz ograniczeń będzie wyglądać następująco:

Zawsze jest tutaj sytuacja taka, że jeden wektor jest wypukłą kombinacją liniową drugiego. W ten sposób takie wektory nigdy nie mogą stać w bazie i tworzyć wektorów bazowych, ponieważ są współliniowe, a zatem macierz byłaby macierzą osobliwą. W ten sposób nie powstałoby rozwiązanie, które generowałoby niezerową wartość np. s₁⁺ i s₁^-.

Jeśli tak jest, to metoda simplex sama z siebie zagwarantuje nam spełnienie „blokady nonsensu”, metoda ta nigdy nie wybierze takiego składu, który zawierałby na liście zmiennych bazowych obie zmienne na raz. Można więc rozwiązywać model zastępczy bez ograniczenia „blokada nonsensu”.

Rozwiązanie tego problemu jest następujące:

x₁^O = 350

x₂^O = 0

s₁⁺ = 50

s₂^- = 100

Wszystkie pozostałe zmienne, nie umieszczone powyżej, jako zmienne niebazowe mają wartość zero.

Decyzja powyższa prowadzi do następującej sytuacji: Cel pierwszy będzie nadszacowany na kwotę 50, czyli otrzymamy 1050. Cel drugi będzie niedoszacowany o 100, czyli zamiast 800 otrzymamy 700. Wartość funkcji celu wyniesie 100 i oznacza ważoną sumę odchyleń od zadanych celów.

Wykład IV

7.III.2003

Klasyczne zagadnienia transportowe i pochodne:

Sytuacja decyzyjna jest pokazana na rysunku:

podaż przewozy zapotrzebowanie

(a_i) (x_ij) (c_ij) (b_j)

m n

punkty nadania punkty odbioru

(i) (j)

(1) b₁ = 70

a₁ = 100 (1)

(2) b₂ = 50

a₂ = 140 (2)

(3) b₃ = 90

a₃ = 110 (3)

4. b₄ = 140

∑ = 350 ∑ = 350

Problem dotyczy przewozu jednorodnego dobra. Mogą to być np. kontenery, czy jakieś zwarte, jednorodne ładunki, które znajdują się w punktach nadania. Z drugiej strony są punkty odbioru, które zgłaszają zapotrzebowanie na pewne ilości dóbr.

Zadanie decyzyjne jest następujące: Ustalić rozmiary przewozu tych wielkości z punktów nadania do punktów odbioru tak, żeby łączny koszt transportu był możliwie najmniejszy.

W naszym przykładzie mamy 3 punkty nadania i 4 punkty odbioru, zatem decyzję trzeba podjąć odnośnie 12 tras. Przy każdym z łuków grafu (inaczej przy każdej strzałce) można zapisać oznaczenia tras, oraz jednostkowe koszty transportu.

Zmiennymi decyzyjnymi będą przewozy, oznaczone jako x_ij, które oznaczają rozmiar przewozu na trasie z i-tego punktu nadania do j-tego punktu odbioru.

Jako c_ij oznaczamy koszty transportu jednostki dobra z i-tego punktu nadania do j-tego punktu odbioru.

W naszym przykładzie występuje sytuacja taka, że
a więc mówimy, że mamy do czynienia z tzw. zamkniętym zagadnieniem transportowym.

W ogólności będziemy formułowali modele do takich zagadnień, gdzie będzie zachodziła relacja:

Tak, jak przystało na rynek, po stronie popytowej - po stronie zapotrzebowania ma prawo być mniej, niż po stronie producenta. Nie rozważamy natomiast relacji odwrotnej, przy rynku producenta.

Model decyzyjny:

Ogólny model klasycznego zagadnienia transportowego jest następujący: Znajdź najmniejszą wartość łącznych kosztów transportu, co zapiszemy następująco:

.

Gdyby nie było innych ograniczeń, to odpowiedź byłaby natychmiastowa: Nic nie woź, to koszty przewozu wyniosą zero, ale ideą zadania jest zaspokojenie potrzeb w punktach odbytu za pomocą tego, co mamy w punktach nadania i trzeba to zrobić jak najtaniej. Jeśli tak, to należy wprowadzić następujące ograniczenia:

Po rozpisaniu model przykładowy wygląda następująco:

Funkcja celu:

Ograniczenia dla punktów nadania:

= 100 u₁

= 140 u₂

= 110 u₃

Ograniczenia dla punktów odbioru:

= 70 v₁

= 50 v₂

= 90 v₃

= 140 v₄

Ograniczenia brzegowe:

Ponieważ podaż równa jest popytowi, to nierówność
została zastąpiona równaniem.

Wyceny dualne w tym modelu zostały oznaczone jako u₁ ... u₃, oraz v₁ ... v₄.

Zmiennych jest 12 - 3 punkty nadania i 4 punkty odbioru. Jest to model liniowy, więc spokojnie możnaby użyć metody simplex, nawet ręcznie. Macierz współczynniku składa się tylko z zer i jedynek, więc nie byłoby z tym problemu. Byłaby to jednak bardzo mozolna i długa metoda.

Z uwagi na specyficzną postać macierzy lewych stron układu, opracowano specjalną metodę znaną pod nazwą klasycznego algorytmu transportowego.

Tw.:

Jeśli parametry modelu w klasycznym zagadnieniu transportowym są liczbami całkowitymi, to rozwiązanie optymalne tego problemu będzie również dane w liczbach całkowitych. Tą własność wykorzystać można w zagadnieniu optymalnego przydziału, o którym będzie mowa później.

W wyjątkowym przypadku może być więcej, niż jedno rozwiązanie optymalne, a zatem jeśli zbudujemy liniową kombinację wypukłą kilku rozwiązań optymalnych, to w wyniku możemy otrzymać liczbę ułamkową. Zawsze jednak istnieje rozwiązanie optymalne dane w liczbach całkowitych, jeśli tylko parametry będą całkowite.

Dowolnie wybrane z siedmiu równań modelu jest liniową kombinacją pozostałych, a więc rząd macierzy A po lewej stronie jest równy dla naszego przykładu 6, a w ogólności:

Tw.:

Wymiar bazy dla klasycznego zagadnienia transportowego o m punktach nadania i n punktach odbioru jest równy m+n-1, co przekłada się na następujące spostrzeżenie: Spośród wszystkich dostępnych tras w rozwiązaniu ogólnym będzie wykorzystane jedynie m+n-1 tras, w naszym przykładzie z dwunastu tylko 6 tras.

Z matematyki wiadomo, że wskaźniki optymalności definiujemy jako różnicę między nakładem, a efektem:

.

Dla zagadnienia transportowego przyjmiemy definicję odwrotną:

Trzeba zatem odwrócić kryterium optymalności. Przy tego typu notacji minimalizacji wszystkie wskaźniki optymalności dla rozwiązania optymalnego muszą być większe, bądź równe zero, a przy maksymalizacji ≤ 0.

Można udowodnić, że składnik z_j daje się przedstawić jako różnica wycen dualnych:

W ogólności wskaźnik optymalności w zagadnieniu transportowym będzie miał podwójną indeksację i będzie równy różnicy efektu i nakładu, zapisanej następująco:

Tak, jak w metodzie simplex, wskaźniki optymalności przyjmują wartość 0 tylko dla zmiennych bazowych.

Rozwiązanie:

Dane do zadania:

KOSZTY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	3	2	5	4	100
Dostawca 2	4	6	3	2	140
Dostawca 3	4	4	5	4	110
Popyt	70	50	90	140	350

W czarnej ramce mamy macierz, oznaczaną jako C = [c_ij] jednostkowych kosztów transportu.

W ten sposób w jednym miejscu są zgrupowane dane o przykładzie.

Dwie następne tabele będą odpowiadały w sensie tablicy simpleksowej tabeli z rozwiązaniem, oraz wierszowi wskaźników optymalności.

W każdej z metod związanych z optymalizacją z użyciem liniowych modeli decyzyjnych mamy do czynienia z przeglądem rozwiązań bazowych. Na początek powinniśmy zaproponować zatem program przewozowy, który będzie bazowym programem przewozowym, czyli ustalić na tych 12 trasach tak przewozy, żeby zaangażować do tego nie więcej, niż 6 tras (najlepiej dokładnie 6). Istnieje wiele metod wyznaczania rozwiązania startowego. Tutaj zajmiemy się tylko metodą kąta północno - zachodniego:

PRZEWOZY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	70				30
Dostawca 2					140
Dostawca 3					110
Popyt	0	50	90	140	350

Zaczynamy od ustalenia przewozu na trasie z rogu położonego w północno - zachodnim rogu (oznaczonego na szaro). Staramy się tutaj ulokować maksymalnie duży przewóz, czyli całą wartość popytu. Po wypełnieniu tego pola pierwszy dostawca ma jeszcze 30 jednostek zapasu.

PRZEWOZY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	70	30			0
Dostawca 2		20			120
Dostawca 3					110
Popyt	0	0	90	140	350

Po zaspokojeniu popytu odbiorcy pierwszego znowu przechodzimy do rogu północno - zachodniego. Maksymalnie w polu tym (oznaczonym kolorem jasnoszarym) może znaleźć się minimum z 30 i 50, czyli 30. Pozostałą część popytu zaspokaja dostawca drugi.

Kontynuując dalej ten proces otrzymujemy następujące rozwiązanie początkowe:

PRZEWOZY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	70	30			100
Dostawca 2		20	90	30	140
Dostawca 3				110	110
Popyt	70	50	90	140	350

Jest to rozwiązanie bazowe, ponieważ wykorzystanych jest m+n-1 = 6 tras. Jest to również rozwiązanie dopuszczalne, ponieważ sumy wierszy i kolumn w czarnej ramce odpowiadają wartościom odpowiednio podaży i zapotrzebowania.

Dla tego programu wartość funkcji celu wyniesie:

Poniżej sprawdzimy, czy jest to najlepszy program przewozowy, czy też można znaleźć tańszy.

Ocena rozwiązania początkowego:

Zaczynamy od tego, iż musimy wyznaczyć wartości wycen dualnych dla tego rozwiązania.

Niewiadomych mamy 7, a równań tylko 6, a więc układ posiada 1 stopień swobody. Jeśli jedno równanie jest liniową kombinacją pozostałych w naszych ograniczeniach, to w zasadzie dowolnie wybraną z wartości u lub v można zastąpić zerem i się nie przejmować. Standartowo będziemy nakładali wartość 0 na zmienną u₁:

	v1	v2	v3	v4	wartości zmiennych ui
u1					0
u2
u3
wartości zmiennych vj					-

Do wyliczenia będzie prosty układ sześciu równań z sześcioma niewiadomymi:

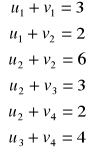
Ogólnie można zapisać go następująco:

Takich równań będzie tyle, ile jest tras, na których są przewozy.

Tabela poniższa pozwala na rozwiązywanie tego układu bez zapisywania go. Rozpoczniemy od tego, że w miejscach odpowiadających zmiennym bazowym zapiszemy jednostkowe koszty transportu z tabeli z danymi:

	v1	v2	v3	v4	wartości zmiennych ui
u1	3	2			0
u2		6	3	2
u3				4
wartości zmiennych vj					-

Liczby brzegowe (czyli wyceny dualne) zsumowane muszą dawać liczbę na przecięciach. Jeśli np. u₁ + v₁ ma być równe 3, a przyjęliśmy u₁ = 0, to v₁ będzie równe 3 itd. W wyniku takich obliczeń otrzymamy poniższą tabelę:

	v1	v2	v3	v4	wartości zmiennych ui
u1	3	2			0
u2		6	3	2	4
u3				4	6
wartości zmiennych vj	3	2	- 1	- 2	-

Mamy zatem rozwiązanie dualne. Zgodnie ze wzorem na wskaźnik optymalności powinniśmy dla wszystkich innych tras wyliczyć wskaźniki optymalności, czyli od kosztów jednostkowych odjąć sumę wycen dualnych. Żeby się łatwiej liczyło, można podzielić pola, w których będą liczone wskaźniki na pół i z lewej strony zapiszemy sumę u_i + v_j, natomiast po prawej stronie już gotowy wskaźnik Δ_ij:

	v1		v2		v3		v4		wartości zmiennych ui
u1	3		2		- 1	6	- 2	2	0
u2	7	- 3	6		3		2		4
u3	9	- 5	8	- 4	5	0	4		6
wartości zmiennych vj	3		2		- 1		- 2		-

Ten program uznać można za optymalny, jeśliby wszystkie wskaźniki optymalności były większe, bądź równe zero. Inne trasy mogą prowadzić do obniżki kosztów. Patrząc na wskaźniki optymalności widzimy, że rozwiązanie początkowe nie jest rozwiązaniem optymalnym, czyli można uzyskać program przewozowy o kosztach niższych niż 1160.

Kryterium wejścia jest takie samo, jak w metodzie simplex - trzeba wybrać tą zmienną, która ma najmniejszy wskaźnik, czyli w naszym przypadku trasę x₃₁:

	v1		v2		v3		v4		wartości zmiennych ui
u1	3		2		- 1	6	- 2	2	0
u2	7	- 3	6		3		2		4
u3	9	- 5	8	- 4	5	0	4		6
wartości zmiennych vj	3		2		- 1		- 2		-

Wskaźnik optymalności równy - 5 oznacza, że jeśli wprowadzimy przewóz na trasę x₃₁, to na każdej przewożonej jednostce koszty spadną o 5 jednostek pieniężnych.

Kolejne rozwiązanie będzie generowane następująco: Trzeba zaznaczyć (w naszym przypadku plusem), że trzeba ulokować przewóz na trasie od dostawcy trzeciego do odbiorcy pierwszego i starać się ulokować tu jak najwięcej.

PRZEWOZY	Odbiorca 1		Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	70		30			100
Dostawca 2			20	90	30	140
Dostawca 3		+			110	110
Popyt	70		50	90	140	350

Jeśli jednak coś dodamy, to burzymy bilans całości. Żeby przeprowadzić w miarę bezpiecznie procedurę korygowania rozwiązania trzeba zbudować tzw. cykl korygujący przewozy. Budowę cyklu korygującego przewozy rozpoczynamy od wykreślenia z tej macierzy wszystkich wierszy i kolumn, które zawierają po jednym przewozie, przy czym trasę oznaczoną, że tam chcemy mieć przewozy traktujemy, jakby już była z przewozami:

PRZEWOZY	Odbiorca 1		Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	70		30			100
Dostawca 2			20	90	30	140
Dostawca 3		+			110	110
Popyt	70		50	90	140	350

Po dokonaniu jakiegoś skreślenia, ponawiamy próbę skreślania wierszy i kolumn tak długo, aż po skończonej liczbie skreśleń pozostaną jakieś wiersze i kolumny nieskreślone. W naszym przykładzie da się wykreślić tylko trzecią kolumnę.

Dalej cykl budujemy według następującej zasady: Zaczynamy od pola zaznaczonego dzięki wskaźnikowi optymalności, a dalej posuwamy się wyłącznie po polach, gdzie są przewozy i oznaczamy korektę in plus lub in minus tak, aby skorygować bilans:

PRZEWOZY	Odbiorca 1		Odbiorca 2		Odbiorca 3	Odbiorca 4		Podaż
Dostawca 1	70	-	30	+				100
Dostawca 2			20	-	90	30	+	140
Dostawca 3		+				110	-	110
Popyt	70		50		90	140		350

Rozwiązanie poprawione:

Budowę nowego rozwiązania zaczynamy od przepisania skreślonych informacji:

PRZEWOZY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1					100
Dostawca 2			90		140
Dostawca 3					110
Popyt	70	50	90	140	350

W naszym przypadku jedyną skreśloną informacją jest przewóz na trasie Dostawca 2 - Odbiorca 3.

Następnie musimy się zastanowić, jaki będzie przewóz na innych trasach. Po pierwsze ile mamy dodawać w miejscach, gdzie są plusy i odejmować w miejscach, gdzie są minusy? Musi być to ta sama liczba. Maksymalna liczba, która może się tu pojawić, czyli wartość x'₃₁ będzie wynikać z tego, co się dzieje w miejscach, gdzie dokonujemy korekty in minus. Ponieważ wszędzie dodajemy i odejmujemy tą samą liczbę, to musi być taka, żeby po dokonaniu tych działań dodawania i odejmowania nigdzie nie powstała liczba ujemna. Będzie to wartość minimalna z wartości zmniejszanych:

Maksymalna dopuszczalna korekta wynosi 20. Wobec tego nowy program przewozowy będzie wyglądał następująco:

PRZEWOZY	Odbiorca 1	Odbiorca 2	Odbiorca 3	Odbiorca 4	Podaż
Dostawca 1	50	50			100
Dostawca 2			90	50	140
Dostawca 3	20			90	110
Popyt	70	50	90	140	350

W miejscach oznaczonych plusem w tabeli z oceną rozwiązania początkowego dodajemy 20, a w miejscach oznaczonych tam minusem odejmujemy 20.

Jest to rozwiązanie bazowe, ponieważ angażuje 6 tras, oraz rozwiązanie dopuszczalne.

Korzystając z definicji wskaźnika optymalności można wyliczyć koszty:

Następnie sprawdzamy, czy rozwiązanie to jest optymalne jak wyżej:

	v1		v2		v3		v4		wartości zmiennych ui
u1	3		2		4	1	3	1	0
u2	2	2	1	5	3		2		- 1
u3	4		3	1	5	0	4		1
wartości zmiennych vj	3		2		4		3		-

Jest to rozwiązanie optymalne, ponieważ wszystkie wskaźniki optymalności są większe, lub równe zero.

Rozwiązanie:

Dostawca 1 - Odbiorca 1 → 50

Dostawca 2 - Odbiorca 2 → 50

Dostawca 2 - Odbiorca 3 → 50

Dostawca 2 - Odbiorca 4 → 50

Dostawca 3 - Odbiorca 1 → 50

Dostawca 3 - Odbiorca 4 → 50

K = 1060

Zagadnienia transportowe z kryterium czasu:

Zagadnienie transportowe z kryterium czasu I rodzaju:

W klasycznym zagadnieniu kosztowym liczby c_ij oznaczały jednostkowe koszty transportu. Natomiast może być inny punkt ciężkości poszukiwania decyzji najlepszej, oraz inne dane. Kogoś może interesować taki przypadek, żeby łączny czas przewozu był najmniejszy. Wtedy liczby wspomniane potraktowalibyśmy jako czasy przewozu jednostki dobra. Jeśliby zamiast kosztów użyć macierzy jednostkowych czasów przewozu T = [t_ij] (czasów przewozu z i-tego punktu nadania do j-tego punktu odbioru) to otrzymamy zagadnienie transportowe z kryterium czasu I rodzaju. Model byłby taki sam, również jego rozwiązanie. Różnica jest tylko w macierzy:

T = [t_ij]

Zagadnienie transportowe z kryterium czasu II rodzaju:

Oznaczenie macierzy jest takie samo, z tym, że macierz T = [t_ij] jest to macierz odległości czasowych. Tutaj nie interesuje nas ile przewozi się na danej trasie, natomiast ważne jest ile czasu zajmuje przemieszczenie pomiędzy i-tym punktem nadania, a j-tym punktem odbioru. Ilość przemieszczanych jednostek jest nieistotna. Jeśli przewozy ruszyłyby jednocześnie, to powinny się zakończyć możliwie jak najszybciej.

Model decyzyjny:

Model formalny nie będzie już liniowym modelem decyzyjnym. Funkcja celu będzie wyglądać następująco:

Chodzi o to, aby znaleźć minimum po wszystkich rozwiązaniach dopuszczalnych, dla których maksymalna z odległości czasowych będzie najmniejsza. Dalsze ograniczenia są takie, jak wyżej:

Przewóz zakończy się wtedy, gdy zostanie przewieziona ostatnia jednostka.

Tego typu zadania mimo, że są z nieliniową funkcją celu, dadzą się również rozwiązywać klasycznym algorytmem transportowym, trzeba tylko dokonać pewnej modyfikacji w macierzy T.

Zagadnienie przydziału:

W modelu tym w macierzy parametrów znajdują się szeroko rozumiane użyteczności. Zmienna decyzyjna będzie definiowana jako zmienna binarna, która przyjmie wartość 1 dla przydziału, lub wartość 0 w przypadku braku przydziału dla danego elementu:

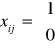
Przy tak zdefiniowanych zmiennych model decyzyjny wygląda następująco:

Ograniczenia wyglądają następująco:

Problem ten można rozwiązywać albo za pomocą specjalnego algorytmu, zwanego algorytmem węgierskim (ang. hungarian method), albo za pomocą zwykłego algorytmu dla zadania transportowego.

Zagadnienie przydziału, ogólnie rzecz biorąc, polega na realizacji celów przy pomocy pewnych środków. Zawsze w boczku albo w główce będą cele, a z drugiej strony będą środki do ich realizacji. Funkcja celu będzie wyrażała pewną użyteczność.

Wykład V

14.III.2003

Podejmowanie decyzji w warunkach niepewności:

Temat ten ilustruje przykład 2.1 z podręcznika „Wybrane metody badań operacyjnych”.

Załóżmy, że decydent chce wybrać spośród trzech różnych możliwości. Jednej decyzji odpowiadają dwa możliwe wyniki, w zależności od tego, jak się zachowa rynek. Są trzy możliwe do przyjęcia decyzje. Razem tworzy to 6 możliwości decyzji. Nie ma żadnej pewności co do tego, która z możliwych decyzji jest najlepsza. Można jedynie podać pewne wskazówki, jak postępować w zależności od tego jaki mamy charakter, oraz przynajmniej w kategoriach wartości oczekiwanych można wskazać na właściwą decyzję. Wynik jest zmienną losową i nie znamy rozkładu prawdopodobieństwa tej zmiennej. Oznacza to, że podejmujemy decyzję w warunkach niepewności. Gdybyśmy znali prawdopodobieństwa wystąpienia określonych stanów natury, czyli rozkład prawdopodobieństwa dla wyników, to decyzja podejmowana byłaby w warunkach ryzyka.

Można informacje dla takich problemów zbierać tabelarycznie, odpowiednikiem tabeli jest macierz i można określić następującą konwencję: W wierszach zawsze będą decyzje, natomiast w kolumnach będą stany natury (stany rynku). Można to również pokazać w formie tzw. drzewa decyzyjnego. Najpopularniejsza obecnie jest forma drzewa decyzyjnego.

Rozważymy tutaj pięć kryteriów:

1. Kryterium hurra optymisty, nazywane również kryterium MaxiMax, czyli maksimum z maksimum. Optymista spojrzałby na 6 możliwości i wybrał maksimum dla każdej decyzji, a następnie maksimum spośród nich.

2. Kryterium człowieka ostrożnego, czyli MaxiMin, nazywane również kryterium Walt'a. Pesymista patrzy, co najgorszego może go spotkać, czyli wybiera minimum zysków przy każdej z decyzji, a następnie z tych kwot gwarantowanych wybiera maksimum.

3. Kryterium Hurwicza, które wypośrodkowuje powyższe dwie skrajne postawy.

Zanim się zastosuje to kryterium, to decydent musi się przy każdej decyzji zdeklarować jaką ma skłonność do ryzyka. Niech będzie to liczba α ∈ <0, 1>. Im bliżej jedynki, tym większa skłonność do ryzyka i odwrotnie. Zero oznacza postępowanie MaxiMin, a 1 postępowanie MaxiMax. Takich wielkości będzie tyle, ile jest decyzji. To są wartości subiektywne.

Następne, co musi zrobić decydent, to dla każdej decyzji obliczyć średnioważony zysk. Wagami są tutaj skłonności do ryzyka (bądź awersie do ryzyka równe 1 - α).

Spośród tych wartości wybieramy taką, która da nam maksymalny zysk.

4. Kryterium Laplace'a: Skoro nie wiemy, jaki jest rozkład prawdopodobieństwa dla wyniku, to jedyne, co można zrobić, to przyjąć, że jest to rozkład równomierny, tzn. przy n stanach rynku każdy otrzymałby szansę równą
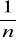
   . Przyjmuje się, że prawdopodobieństwo wystąpienia każdego stanu rynku jest takie samo. Dalej liczy się wartości oczekiwane zmiennej losowej dyskretnej.

5. Kryterium Savage'a, które odwraca skrajne postępowanie asekuranta (MaxiMin) i będzie mowa nie o maksymalizacji minimalnych zysków, tylko będzie minimalizowało maksymalne straty. Ono jest nazywane również MiniMax dogodnej straty, lub MiniMax żalu.

Podstawą wyboru jest tzw. macierz żalu R budowana kolejnymi kolumnami. Patrząc na macierz żalu decydent wybiera maksima przy danych stanach rynku, a następnie określa straty w stosunku do innych najlepszych decyzji. Kryterium to staje się odwróceniem kryterium MaxiMin.

Podejmowanie decyzji w warunkach ryzyka:

Pojawi się tutaj nowa informacja o prawdopodobieństwach wystąpienia poszczególnych stanów na rynku, nazywanych prawdopodobieństwami a priori, czyli ustalonymi z góry na podstawie źródła, np. poprzednich informacji, albo jakiś badań pilotażowych. W odróżnieniu od kryterium Laplace'a są to już konkretne, różne od siebie liczby. Mamy zatem rozkład prawdopodobieństwa dla stanów rynku.

Tutaj będziemy rozpatrywali dwa kryteria:

1. Kryterium maksymalnej oczekiwanej wartości. Liczymy tutaj wartości oczekiwane zysku przy poszczególnych decyzjach i wybieramy spośród nich najlepszą o maksymalnej oczekiwanej wartości zysku.

2. Kryterium minimalnego oczekiwanego żalu, w którym wykorzystujemy, zamiast macierzy zysków, macierz żalu taką, jak w przypadku kryterium Savage'a. Z tej macierzy liczymy odpowiednie wartości oczekiwane żalu, z których wybieramy najmniejszą.

Działając w warunkach ryzyka będziemy wykorzystywali wyłącznie pojęcie wartości oczekiwanych, które odniesiemy albo do zysków, albo do strat. Za każdym razem wykorzystamy wartość oczekiwaną zmiennej losowej skokowej do wyznaczenia oczekiwanej wartości bądź zysku, bądź straty. Będziemy postępować zgodnie ze zdrowym rozsądkiem: W przypadku, gdy będzie chodziło o macierz zysku, będziemy wybierać największą wartość oczekiwaną, a przy żalu odwrotnie - będziemy starać się minimalizować straty w stosunku do najlepszych decyzji, a więc wybierzemy najniższą wartość oczekiwaną.

Cena graniczna doskonałej informacji:

Cena graniczna doskonałej (perfekcyjnej) informacji jest to postępowanie następujące: Gdyby decydent mógł podjąć decyzję prawidłową według tego, co będzie w przyszłości, co jest nierealne, to działałby właśnie w warunkach perfekcyjnej informacji. Podejmując decyzję w tej hipotetycznej sytuacji, kiedy możemy podglądać przyszłość oczekiwany zysk wyniósłby dokładnie tyle co wartość oczekiwana, gdyż prawdopodobieństwa wystąpienia stanów natury są w tym przypadku całkowicie zgodne z rzeczywistością. Różnica pomiędzy tak uzyskaną wartością, a wartością oczekiwaną wyliczoną według kryterium maksymalnej oczekiwanej wartości i minimalnego oczekiwanego żalu jest to właśnie cena graniczna doskonałej informacji.

Nie opłaca nam się płacić więcej za kreowanie przyszłości (działania marketingowe, badania rynku etc.), niż wynosi tak obliczona cena graniczna perfekcyjnej informacji. Cena graniczna doskonałej informacji jest zawsze równa minimalnemu oczekiwanemu żalowi. Jest to oczywiście informacja skrajna.

Podejmowanie decyzji z wykorzystaniem dodatkowej informacji:

Dane mamy wskaźniki struktury tworzące pewne dodatkowe informacje. Należy ją tak wykorzystać, aby ułatwiło to pierwotny wybór. Z punktu widzenia decydenta informacje dodatkowe można potraktować jako prawdopodobieństwa warunkowe wystąpienia czynnika przy danych stanach natury. Dysponujemy rozkładami warunkowymi wystąpienia czynników przy warunkach określających różne stany natury. Nas interesuje prawdopodobieństwo wystąpienia danego stanu natury przy warunku, że zadziała jeden z czynników dodatkowych. Należy więc przerobić prawdopodobieństwa a priori na prawdopodobieństwa a posteriori.

W następnym kroku liczymy jakie odbicie będą miały te prawdopodobieństwa a posteriori w naszym zysku. Z tych prawdopodobieństw wyliczamy wartości oczekiwane dla różnych stanów natury, które określają nasze zyski. Spośród wszystkich możliwości wybieramy największą. Cały proces powtarzamy tyle razy, ile mamy czynników dodatkowych.

Mając te informacje możemy policzyć tzw. oczekiwaną korzyść z dodatkowej informacji. Otrzymujemy ją po wyliczeniu wartości oczekiwanej, spośród wszystkich wartości oczekiwanych przy różnych wariantach informacji dodatkowej. Będzie to różnica pomiędzy oczekiwanym zyskiem osiągniętym przy dodatkowej informacji a kwotą, jaką uzyskujemy bez żadnych dodatkowej informacji.

Efektywność takiego postępowania oceniana jest jako stosunek oczekiwanej korzyści z dodatkowej informacji do ceny granicznej perfekcyjnej informacji.

Należy jeszcze skorygować to o cenę dodatkowej informacji. Należy zastanowić się, czy koszt uzyskania dodatkowych informacji nie jest wyższy niż oczekiwana korzyść z tych informacji. Dla łatwości obliczeń przyjmujemy zerowe koszty tego postępowania, natomiast w rzeczywistości trzeba to uwzględnić.

Wykład VII

28.III.2003

Metoda PERT:

Założyć należy, że czas trwania każdej czynności jest zmienną losową o rozkładzie β. Rozkład beta może być symetryczny, albo asymetryczny, w zależności od jego parametrów.

Na to, aby uruchomić całe postępowanie klasycznej metody PERT wystarczy, że eksperci podadzą nam dla każdej czynności następujące informacje: najkrótszy czas trwania czynności zwany czasem optymistycznym, najdłuższy czas trwania czynności nazywany często pesymistycznym i najbardziej prawdopodobny czas wykonania czynności, czyli dominantę, dla której funkcja gęstości osiąga swoje maksimum. Poniżej czasu optymistycznego i powyżej czasu pesymistycznego wykres pokrywa się z linią czasu, czyli są to wartości niemożliwe do uzyskania.

Jak już mamy oceny ekspertów dla każdej czynności z osobna, to możemy obliczyć dla nich estymatory - wartość oczekiwaną i wariancję. Jest to analiza wstępna.

Następnie przechodzimy do identycznych obliczeń, jakie mają miejsce przy metodzie CPM. Zaczynając od pierwszej czynności, obliczamy wartość oczekiwaną terminu końcowego. Potem wstawiamy jako termin dyrektywny obliczoną wartość terminu końcowego i odwrócić obliczenia, aż dojdziemy do początku. Po przeprowadzeniu tych obliczeń zgodnie z techniką pokazaną dla modelu CPM możemy zbudować sobie harmonogram przedsięwzięcia. Znajdujemy w ten sposób ścieżkę krytyczną.

Różnica między metodą PERT a CPM polega na tym, że termin zajścia znaczenia końcowego nie jest stałą, tylko też jest zmienną losową, ponieważ jest sumą zmiennych losowych.

Centralne twierdzenie graniczne:

Suma, bądź różnica niezależnych zmiennych losowych o tych samych rozkładach jest również zmienną losową o rozkładzie asymptotycznie normalnym, czyli im więcej jest sumowanych zmiennych, tym lepsze jest przybliżenie do rozkładu normalnego. Zmienna ta ma wartość oczekiwaną równą sumie (bądź różnicy) wartości oczekiwanych, natomiast wariancję zawsze ma równą sumie wariancji splatanych ze sobą zmiennych.

W metodzie PERT interesują nas tylko te czynności, które są czynnościami krytycznymi.

Prawdopodobieństwem dotrzymania terminu określonego przez wartość oczekiwaną terminu końcowego jest równa wartości wystandaryzowanej dystrybuanty φ(0) = ½, czyli 50 %. Szansę dotrzymania dowolnego terminu dyrektywnego obliczamy jako wartość dystrybuanty rozkładu normalnego odpowiedniej wystandaryzowanej zmiennej losowej.

Od strony praktycznego wykorzystania tej metody dopracowano się rzeczy następującej: Termin dyrektywny powinien być tak dobierany, iżby szansa jego dotrzymania mieściła się w przedziale od ok. 30% do ok. 60%. Jeśli ktoś będzie forsował termin dyrektywny, którego szansa będzie mniejsza od 30%, to kogoś takiego nazwiemy ryzykantem. Nie powinno się dobierać terminów dyrektywnych o szansie wykonania wyraźnie mniejszej, niż 30%. Nie powinno się również forsować terminów dyrektywnych, których szansa dotrzymania byłaby wyraźnie większa od 60%, bo byłoby to nadmierne asekuranctwo.

Należy więc obliczyć przedział od terminu dyrektywnego minimalnego do maksymalnego, na którym będą opierać się negocjacje. Dla terminu dyrektywnego należy rozwiązać następujący problem:

φ(td_min) = 0,3

φ(td_max) = 0,6

Produktem końcowym w metodzie PERT oprócz tego, co było w metodzie CPM (harmonogram przedsięwzięcia, wąskie gardła, ścieżka krytyczna) są informacje dotyczące prawdopodobieństwa dotrzymania terminu dyrektywnego.

Metoda LESS:

W metodzie LESS założenia są następujące:

1. Czas trwania każdej czynności jest zdeterminowany.

2. Dla każdej czynności mamy oszacowane następujące informacje:

• Normalny czas wykonywania czynności, przy normalnych nakładach kapitałowych na jej wykonanie.

• Koszty związane z tym normalnym czasem.

• Czas graniczny, czyli najkrótszy możliwy czas, w którym można taką czynność wykonać.

• Koszty wykonania związane z czasem granicznym.

Możemy wykonywać czynność w czasie normalnym i wówczas ponosimy niezbyt duże koszty, nazywane kosztami normalnymi. Możemy skracać czas wykonania czynności, czyli akcelerować tę czynność, do osiągnięcia czasu granicznego. Żeby robić czynność szybciej, należy ponieść większe nakłady, a zatem tutaj koszty graniczne będą zdecydowanie większe.

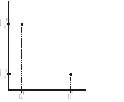
Żeby przeprowadzić postępowanie metody LESS powinniśmy znać funkcję kosztów wykonania czynności, która będzie przechodziła przez punkty zaznaczone powyżej. Tu następuje pierwsze uproszczenie. Nie mamy żadnego materiału statystycznego, ani jego opracowania w postaci funkcji. Jeśli tak, to zakłada się , że ten związek ma charakter liniowy i proponuje się interpolację funkcji liniowej między tymi punktami, a zatem zakłada się, że wykres tej nieznanej funkcji kosztów dla każdej czynności jest wykresem liniowym.

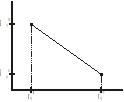
Jeśli tak, to możemy dla każdej czynności obliczyć tzw. jednostkowy koszt akceleracji jako stosunek przyrostu kosztów do przyrostu czasu:

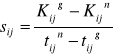
W metodzie LESS chodzi nam o dwie rzeczy jednocześnie. W metodzie CPM funkcję celu zapisywaliśmy jako: Zminimalizuj termin końcowy. W metodzie LESS będzie to samo, ale do tego dojdzie jeszcze żądanie minimalizacji kosztów całkowitych przedsięwzięcia. Problem w metodzie LESS jest problemem dwukryteriowym. Jeśli należałoby nadać hierarchię tym dwóm kryteriom, to oczywiście pierwszym i ważniejszym kryterium kosztów, drugim jest kryterium czasu trwania czynności.

Im bardziej będziemy akcelerować czasy wykonania czynności, czyli im krótsze będą one od czasów normalnych, tym większe będą koszty, ale za to będzie krótszy termin końcowy. Gdzieś pomiędzy leży „złoty środek”, który mamy znaleźć.

Funkcja kosztów całkowitych jest to suma kosztów bezpośrednich i kosztów pośrednich. Koszty bezpośrednie będą związane wyłącznie z realizacją czynności, natomiast koszty pośrednie będą związane z przedsięwzięciem jako całością, a nie z każdą z czynności osobno. Im przedsięwzięcie trwa dłużej, tym koszty bezpośrednie są mniejsze, a zatem koszty te są malejącą funkcją czasu. Koszty pośrednie natomiast są rosnącą funkcją czasu. W sumie otrzymamy dla kosztów całkowitych klasyczną funkcję kosztów, jako funkcję trwania kosztów przedsięwzięcia. Funkcja ta (przynajmniej w okolicy ekstremum) jest dobrze aproksymowana funkcją kwadratową:

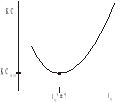
Naszym zadaniem w metodzie LESS będzie znalezienie takiego terminu końcowego, przy którym koszty całkowite będą minimalne. Można tutaj zbudować liniowy model decyzyjny i go rozwiązać. My natomiast poprzestaniemy na tzw. ręcznej metodzie LESS, gdzie siedząc przy komputerze i mając możliwość szybkich zmian czasów trwania poszczególnych czynności i przeliczania harmonogramu przedsięwzięcia, nie będziemy budować żadnego modelu, tylko przeprowadzimy postępowanie krok po kroku. Po kolei będziemy starali się przechodzić na coraz krótszy termin końcowy (przejście musi być najtańsze z możliwych) i będziemy przyspieszali całe przedsięwzięcie tak długo, dopóki koszty całkowite będą spadały. Kiedy koszty całkowite wzrosną, to zatrzymujemy postępowanie i bierzemy to, co mieliśmy poprzednio.

Przy każdej informacji mamy zapisaną taką trójkę: Normalny czas, graniczny czas i jednostkowy koszt przyspieszenia: (t_ij, t_ij*, s_ij). Na początku wszystkie czynności są wykonywane w czasie normalnym. Na początku trzeba wyliczyć te jednostkowe koszty akceleracji.

Reguły postępowania z ręczną metodą LESS:

1. Przyspieszając czas trwania przedsięwzięcia o jedną jednostkę w grę mogą wchodzić tylko czynności krytyczne. Nie możemy zmniejszać czynności niekrytycznych, bo tylko zwiększymy im zapas czasu i nie zmieni się termin końcowy.

2. Spośród czynności krytycznych wybieramy czynność o najniższym jednostkowym koszcie akceleracji.

3. Jeśli jest więcej, niż jedna ścieżka krytyczna, to przyspieszając wybraną najtańszą czynność krytyczną, trzeba również przyspieszyć równoległą czynność krytyczną.

Kończąc metodę LESS należy przedstawić informację o optymalnych czasach trwania poszczególnych czynności. Na ogół będą to czynności o normalnych czasach trwania i tylko dla czynności krytycznych przyspieszonych ten czas będzie odpowiednio krótszy.

W ramach zarządzania projektami poznaliśmy trzy metody:

• Najprostszą z możliwych metodę CPM, w której zakłada się, że czasy trwania czynności są zdeterminowane,

• Nieco tylko bardziej złożoną metodę PERT, gdzie zakłada się, że przynajmniej jedna z czynności ma losowy czas trwania. Na ogół, jeśli ma jedna, to ma większość,

• W metodzie LESS oprócz harmonogramu, wyłapywania wąskich gardeł i realizowania przedsięwzięcia w najkrótszym możliwym czasie, dokładamy jedno kryterium, będące kryterium nadrzędnym: minimalizację kosztów.

Teoria masowej obsługi:

Tutaj ograniczymy się do najprostszych elementów teorii masowej obsługi.

Mamy do czynienia z dwoma procesami: proces obsługi i proces nadchodzenia zgłoszeń do tej usługi. Zgłoszenia te nadchodzą masowo (przy n → ∞). Teoria masowej obsługi jest to narzędzie, które pozwala dokonywać poprawek w procesach produkcyjnych o charakterze masowym i wszelkich tego typu procesach, np. organizacji stanowisk. To dotyczy takich sytuacji, gdzie zgłoszenia nadchodzą masowo i są obsługiwane przez tzw. aparaty obsługi.

Zgłoszenia nadchodzące ustawiają się w kolejkę. Mogą też zrezygnować z tej kolejki i w ogóle obsługi.

Najprostsze systemy masowej obsługi to:

• Systemy szeregowe - takie, gdzie nadchodzą zgłoszenia, ustawiają się w kolejce i z kolejki każde kolejne zgłoszenie przechodzi do wszystkich aparatów obsługi po kolei - przechodzi przez taki ciąg.

• Systemy równoległe, gdzie zdarzenia nadchodzą, ustawiają się w kolejce i według pewnej reguły z tej kolejki przechodzą do jednego z aparatów obsługi. Wszystkie aparaty obsługi świadczą tutaj te same usługi. Przykładem mogą być kasy sklepowe.

W życiu najczęściej spotykane są systemy mieszane. My ograniczymy się w zasadzie do systemów równoległych z jednym kanałem obsługi, albo z k kanałami obsługi.

Klasyfikacje systemów:

1. Systemy szeregowe, równoległe i mieszane, jak wyżej.

2. Systemy ze stratami i bez strat. Zależy to, czy zgłoszenie opuści system nieobsłużone, czy obsłużone. W przypadku systemu bez strat kiedy zgłoszenie raz wejdzie w kolejkę, to już nie ma możliwości wyjścia z niej, zanim nie przejdzie przez wszystkie aparaty obsługi.

3. Istnienie kolejki: Kolejka może być zabroniona, albo nie zabroniona.

4. Rozmiary kolejki: Kolejka może być ograniczona, albo nieograniczona.

5. Organizacja kolejki. Najsprawiedliwsza jest kolejka FIFO (First-In-First-Out), ale może być kolejka LIFO (Last-In-First-Out), albo SIRO (Selection-In-Random-Order), czyli wybór losowy.

Charakterystyki liczbowe systemów masowej obsługi:

Podstawowe charakterystyki od strony nadchodzenia zgłoszeń są to pewne średnie, które opisują tenże strumień zgłoszeń.

Stopa zgłoszeń λ jest to liczba zgłoszeń, jaka średnio napływa do systemu w danej jednostce czasu:

Można również badać odwrotność stopy zgłoszeń, czyli intensywność zgłoszeń
- odstęp czasu pomiędzy dwoma kolejnymi zgłoszeniami.

Dużo wygodniej i praktyczniej jest operować stopą zgłoszeń. Jeśli chodzi o pomiar, to dużo łatwiej jest ustalić sobie przedział czasu i rejestrować liczbę nadchodzących zgłoszeń w ciągu tej jednostki czasu, aby zebrać materiał statystyczny.

Od strony obsługi można postąpić identycznie - opisywać albo liczbą zgłoszeń obsłużonych w jednostce czasu, albo czasem obsługi. Będzie to stopa obsługi, czyli μ, albo intensywność obsługi, czyli
.

Jeśli teraz mamy informacje o średniej liczbie zgłoszeń nadchodzących w jednostce czasu i średniej liczbie zgłoszeń obsłużonych w tej jednostce czasu, to fundamentalną charakterystyką liczbową w systemach masowej obsługi jest tzw. intensywność ruchu, zwana inaczej stałą Erlanga:

, gdzie s jest to liczba równoległych kanałów obsługi.

Jest to stosunek liczby zgłoszeń napływających do systemu do liczby zgłoszeń obsługiwanych przez system.

Żeby system się nie zatkał, to stała ta musi być mniejsza od jedności:

Kolejka w takim przypadku wydłuża się w nieskończoność i należy dołożyć aparat(y) obsługi. Jeśli współczynnik ten wynosi 1, to będzie on petryfikował, czyli ustalał stan początkowy układu.

Na całym Świecie modele masowej obsługi są kodowane w jednolity sposób. To kodowanie polega na zapisie symbolu rozkładu prawdopodobieństwa dla nadchodzenia zgłoszeń, symbolu rozkładu czasu trwania obsługi na pojedynczym stanowisku, oraz liczbę równoległych kanałów obsługi. Opcjonalnie można jeszcze dopisać informację o rozmiarach populacji (czy będzie ograniczona, czy nieograniczona), oraz io maksymalnej długości kolejki, jaka może nastąpić:

Jest to kodowanie modelu według Kendalla.

Wszystkie modele są dokładnie opisane.

Znać należy model M / M / 1 (∞, ∞)!

Oznacza to, że odstęp między zgłoszeniami jest wykładniczy, albo też ma rozkład Poissona, czas obsługi jest rozkładem wykładniczym, mamy do czynienia z jednym kanałem obsługi, populacja jest nieograniczona, a kolejka jest nieskończona.

Chodzi oczywiście o punkty odbioru .

Laplace Pierre Simon de (1749-1827), wybitny matematyk, fizyk i astronom francuski, profesor Akademii Wojskowej w Paryżu (od 1772), członek AN (od 1785), dyrektor Urzędu Miar i Wag w Paryżu (po 1790), w 1799 piastował urząd ministra spraw wewnętrznych, w 1803 był wiceprzewodniczącym Senatu Francji, w 1817 otrzymał tytuł markiza i para Francji.

Twórca współczesnego ujęcia rachunku prawdopodobieństwa, autor prac z dziedziny rachunku różniczkowego, operatorowego (laplasjan) i teorii wyznaczników, opracował teorię funkcji kulistych, rozwinął klasyczną mechanikę nieba, zaproponował model powstania Układu Słonecznego (według Laplace'a Układ Słoneczny miał powstać z pierwotnej mgławicy), sformułował teorię kapilarności (kapilarne zjawiska), zajmował się teorią powszechnego ciążenia, podał metodę wyznaczania prędkości dźwięku w powietrzu.

30

---