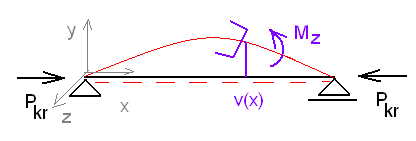
STATECZNOŚĆ
stany równowagi:
obojętna
trwała
chwiejna
ZAKRES SPRĘŻYSTY
M
x
'
v ( x)
z (
)
=
M ( x) = − P ⋅ v x kr
( )
EJ z
− P
'
v ( x)
KR
=
⋅ v( x)
v ( x) = A sin kx + B cos kx EJ z
szukane: k,
A / B
z warunków brzegowych
2
π EJz
P
=
gdzie:
J = J
KR
(
z
min
lw )2
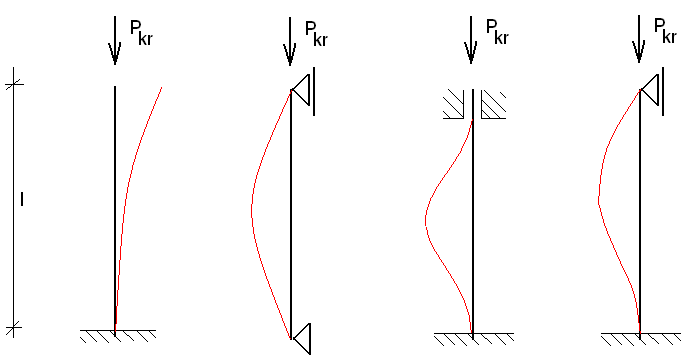
l
l
l
= 2 l
l
= l
l
=
l =
w
w
w
2
w
2
2
2
P
π EJ
i
l
E
KR
min
2
min
σ =
=
= π
λ :
w
=
A
( )
E
2
l
A l
i
w
min
w
π E
E
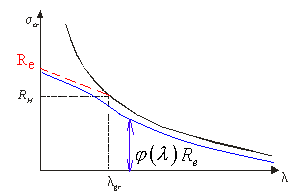
σ (λ)
2
=
λ > λ
2
λ
gr
λ = λ ⇒ σ =
E
R
λ = π
gr
E
H
gr
RH
−
R − R
R
T J
σ
(λ)
e
H
H
= R −
⋅λ
λ < λ
e
π
E
gr
czerwona linia
niebieska linia
KR
σ (λ) =ϕ (λ)⋅ R
ϕ (λ) ≤1
e
KR
ϕ (λ) σ (λ)
:=
Re
λ
π
> λ
E
ϕ (λ)
2
=
gr
2
R λ
e
λ < λ
R − R
R
ϕ (λ) =1 e
H
H
−
⋅λ
gr
R π
E
e
Wytrzymałościowy warunek projektowania: P
≤
ϕ (λ)
Re
⋅
A
NORMA
π
E
λ =
p
1.15
fd
Tabela
λλ 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 …… 1.65 1.90 2.20
p
ϕ λ
λ 0.93 0.89 0.85 0.80 0.74 0.68 0.59 0.5 ……. 0.328 0.257 0.197
p
Projektowanie wg normy:
P
≤ f
d
A ⋅ϕ λ
λ
p
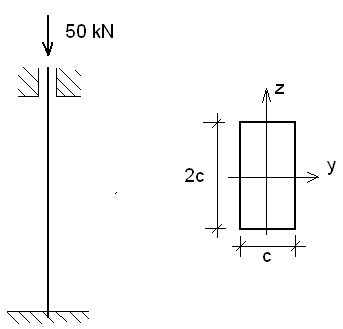
ZADANIE 1.
Zaprojektować pręt ściskany ze względu na zadane obciążenie krytyczne P = 50 kN .
Dane:
l = 4 m , λ = 107 , E = 200 GPa ,
σ
= 240 − 0.56
−
λ [ MPa].
gr
T J
4
4
2 c
c
4
J
c
c
l
J
=
=
min
i
=
=
=
l =
= m
min
12
6
min
2
A
6 ⋅
2
2 c
w
12
2
Przypuszczamy zakres sprężysty 2
6
4
π EJ
3.14 ⋅ 200 ⋅10 ⋅ c
min
P =
=
= 50
c
−
⇒ =
⋅
m
kr
2
l
6 ⋅
2
2.79 10
4
w
l
2 12
w
λ =
=
= 248 > λ
2
i
2.79 ⋅
10−
gr
min
4
4
8 c
2 c
c
J =
=
i =
y
12
3
y
3
l
2 3
w
λ = =
=124 > λ
y
2
i
2.79 ⋅
10−
gr
y
Przypuszczenie było prawdziwe, poprawnie zaprojektowany parametr c.
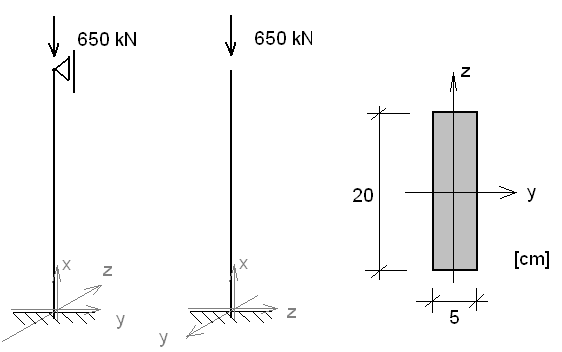
ZADANIE 2.
Obliczyć zapas nośności dla pręta. Dane: E = 200 GPa , R = 150 MPa , H
l = 3 m , σ
= 240 − 0.56
−
λ [ MPa].
T J
3
E
200 10
λ
π
⋅
=
= 3.14
=114.7
−
−
4
2
2
A = 5 ⋅ 20 ⋅10 = 1⋅10 m
gr
R
150
H
2
20 ⋅10−
l
⋅
wy
2 3
l
= 2 l = 6 m
−
2
i =
= 5.77 ⋅10 m
λ =
=
=104 < λ
wy
y
y
−
gr
12
2
i
5.77 ⋅
10
y
P
= σ
⋅ A =
−
⋅
⋅ ⋅ ⋅
⋅
=
−
(
)
4
−
2
240 0.56 104 5 20 10 [ MPa m ] 1818 kN
KR
T J
l
3
2
5 ⋅10−
l
3
l
=
=
m
−
2
i =
=1.44⋅10 m
wz
λ =
=
=147.3 > λ
wz
z
z
−
gr
2
2
12
2
i
1.41⋅1.44 ⋅
10
z
2
π EJz
P
=
= 910 kN
KR
2
lwz
P
min (1818 kN, 910 kN ) n :
KR
=
n =
=1.4
P
650 kN
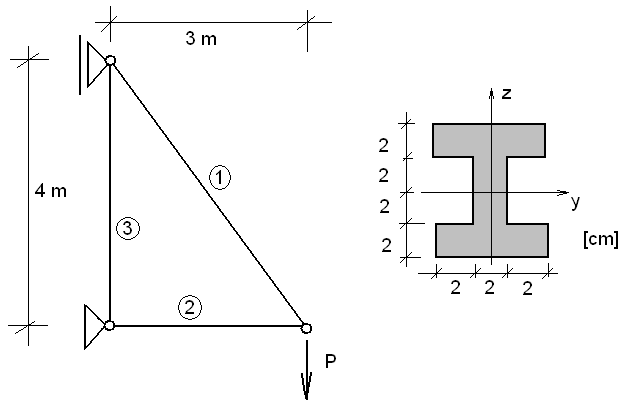
ZADANIE 3.
Obliczyć dopuszczalne obciążenie kratownicy ze względu na stateczność.
5
3
Rozwiązanie statyki:
S = P
S = − P
S = − P
1
4
2
4
3
Charakterystyki geometryczne:
3
3
6 ⋅ 2
2 ⋅ 4
3
3
8 ⋅ 2
4 ⋅ 4
4
J = 2 ⋅
+
= 74.67 cm
4
J =
+
= 234.67 cm > J
z
12
12
y
12
12
z
2
A = 32 cm
i
=1.57 cm
min
3
E
200 10
Materiał: λ
π
⋅
=
= 3.14
=104.72
gr
R
180
H
Pręty ściskane : pręt 2, pręt 3 sprawdzane na stateczność Pręt 2
l
3
l = l = 3 m
w
λ =
=
=196.4 > λ
w
−2
i
1.57 ⋅
10
gr
min
π EJ
3
z
P
=
= S = P
KR
2
2
l
4
w
2
4π
−
EJ
4 ⋅
⋅
⋅
⋅
⋅
z
(3.14)2
6
8
200 10 74.67 10
⇒ P =
=
= 218.36 kN
2
3 l
⋅
w
3 (3)2
Pręt 3
l
4
l = l = 4 m
w
λ =
=
= 261.86 > λ
w
−2
i
1.57 ⋅
10
gr
min
2
π EJ
z
P
=
= S = P
KR
2
3
lw
2
π
−
EJ
⋅
⋅
⋅
⋅
z
(3.14)2
6
8
200 10 74.67 10
⇒ P =
=
= 92.12 kN
2
lw
(3)2
P
= min( P) = 92.12 kN
KR
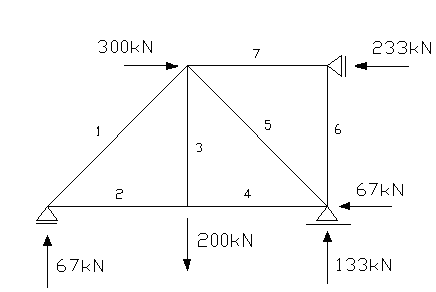
Zadanie 4.
Zaprojektować na stateczność w/g normy pręty kratownicy obciążonej jak na rysunku o przekroju pokazanym na rysunku l = 3.0 m
.
Rozwiązanie statyki:
F = −94.8 kN , F = F = 6
+ 7.0 kN, F = +200 kN, F = −188 kN, F = 0 kN
1
x
x 2
x 4
x 3
x 5
x 6
F = −233 kN
x 7
2
A = 0.89 a kN ,
4
J = J = 0.08 a , i = i = 0.3 a y
z
y
z
Projektowanie prętów rozciąganych:
Fx 2 ≤ R
a ≥ 0.02 m
H
A
Fx 3 ≤ R
a ≥ 0.03 m
H
A
Projektowanie prętów ściskanych: F
π
E
pręt 5
≤
λ =
= 87.37
p
A ϕ ( x 5
fd
λ /λ
1.15
f
p )
d
−
przyjmuję: a = 0.07 m , l = l = 4.24 m 4
2
F = 43.61⋅10 m
w
λ = 201.9
λ
=
λ
2.30
ϕ
=
λ
0.181
λ
p
p
F
188
=
=
⋅
≤
⋅
A ϕ ( x 5
λ /λ
−
⋅
⋅
p )
3
3
238 10
205 10
4
0.181 43.61 10
−
przyjmuję:
a = 0.073 m ,
4
2
F = 47.42 ⋅10 m
λ =193.6
λ
=
λ
2.20
ϕ
=
λ
0.197
λ
p
p
188
=
=
⋅
≤
⋅
A ϕ ( x 5
λ /λ
−
⋅
⋅
p )
3
3
201.2 10
205 10
4
0.197 47.42 10
F
π
E
pręt 7
≤
λ =
= 87.37
p
A ϕ ( x 7
fd
λ /λ
1.15
f
p )
d
−
przyjmuję:
a = 0.07 m , l = l = 3.0 m , 4
2
F = 43.61⋅10 m
w
λ =142.86
λ
=
λ
1.65
ϕ
=
λ
0.328
λ
p
p
F
233
=
=
⋅
≤
⋅
A ϕ ( x 7
λ / λ
−
⋅
⋅
p )
3
3
162.9 10
205 10
4
0.328 43.61 10
−
przyjmuję: a = 0.06 m ,
4
2
F = 32.04 ⋅10 m
λ =166.6
=
λ
1.90
ϕ
=
λ
0.257
λ
p
p
F
233
=
=
⋅
>
⋅
A ϕ ( x 7
λ /λ
−
⋅
⋅
p )
3
3
282.9 10
205 10
4
0.257 32.04 10
−
przyjmuję:
a = 0.068 m ,
4
2
F = 41.15 ⋅10 m
λ =147.1
λ
=
λ
1.68
ϕ
=
λ
0.312
λ
p
p
F
233
=
=
⋅
≤
⋅
A ϕ ( x 7
λ /λ
−
⋅
⋅
p )
3
3
181.5 10
205 10
4
0.312 41.15 10
zadanie 3
W kratownicy przedstawionej na rysunku pas dolny wykonany jest z kątownika L 65 × 65× 8, a pozostałe pręty z kątownika L 50 × 50 × 5. Obliczyć dopuszczalną wartość siły P.
pas dolny: L 65 × 65× 8
2
A = 9.87 cm ,
i
=1.27 cm
min
pozostałe pręty: L 50 × 50 × 5
2
A = 4.8 cm ,
i
= 0.98 cm
min
Materiał: stal, E=205 GPa, Re=215 MPa, RH=190 MPa .
W pasie dolnym największa siła ściskająca S = 3 P
1
N ≤ϕ(λ)⋅ R e
A
E
π ⋅ E
dla λ > λ = π
ϕ (λ)
2
=
gr
R
2
λ ⋅
R
H
e
R − R
R
dla λ < λ
ϕ (λ) =1 e
H
H
−
⋅λ
gr
π ⋅
R
E
e
l
3
205 10
w
λ =
λ
π
⋅
=
=103.19
min ( i , i
gr
190
y
z )
1.2
Dla pręta 1
λ =
= 94.49
λ < λ
1
0.0127
1
gr
215 190
190
ϕ λ
−
=1−
⋅94.49 = 0.894
1 ( 1 )
3
3.14 ⋅ 215 205 ⋅
10
3 P
3
≤ 0.894⋅ 215⋅10
⇒ P ≤
kN
4
9.87 ⋅
63.24
10−
Dla pozostałych prętów , największa siła ściskająca S = P
3
1.2
λ =
=122.45 > λ =103.19
λ > λ
3
0.0098
gr
3
gr
2
3
π 205 10
ϕ λ
⋅
⋅
=
= 0.628
3 (
3 )
(122.45)2 ⋅215
P
3
≤ 0.628⋅ 215⋅10
⇒ P ≤
kN
4
4.8 ⋅
64.81
10−
Siła jest mniejszą z rozważanych dwóch czyli: P ≤ 63.24 kN
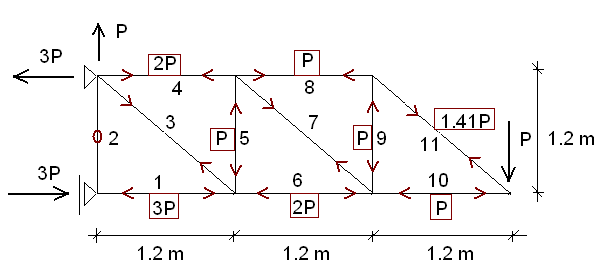
zadanie 4
Dane: E=200 GPa, Re=280 MPa, RH=200 MPa
1. Które pręty się wyboczą?
2. Oblicz nośność konstrukcji ze względu na wyboczenie 3. W jakim zakresie pracują pręty
λ
4. Szukane a , takie aby
gr
λ =
dla pręta najbardziej podatnego na wyboczenie. obliczyć siłę 2
działającą w tym pręcie
KOLOKWIUM NR 3 – PRZYKŁADOWE ZADANIA
Zestaw 1
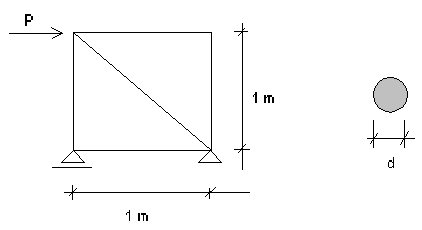
1. Podaj dopuszczalne obciążenie kratownicy, ze względu na wyboczenie prętów ściskanych.
Wymiary kratownicy podane są na rysunku. Pręty mają przekrój kołowy o średnicy d=8cm.
Materiał: stal, E=200 GPa, Re=200 MPa, RH=180 MPa .
Zestaw 2
1. Podaj dopuszczalne obciążenie kratownicy, ze względu na wyboczenie prętów ściskanych.
Wymiary kratownicy podane są na rysunku. Pręty mają przekrój kołowy o średnicy d=8cm.
Materiał: stal, E=200 GPa, Re=200 MPa, RH=180 MPa .