Termodynamika ćw 1,2

Gaz doskonały - gaz, w którym nie istnieją siły przyciągania międzycząsteczkowego, a objętość cząsteczki Prawo Avogadra -przy jednakowej temperaturze i równa jest zeru.

ciśnieniu różne gazy doskonałe mają tę samą ilość cząsteczek w równych objętościach

PRAWA GAZÓW DOSKONAŁYCH

n = n

1

2

Określają zależności między parametrami czynnika termodynamicznego.

m

M

1

1

=

m

M

2

2

Prawo Boyle′a- Mariotte′a (przemiana izotermiczna) -

iloczyn ciśnień i objętości właściwej gazu przy stałej Mϑ = Φ = const

temperaturze jest wielkością stałą.

T = const (dla m = 1 kg gazu) Warunki normalne fizyczne

TN=273,15K

tN=0oC

p ϑ = p ϑ = const

1

1

2

2

pN=101325Pa

pN=760mmHg

p

ϑ

Φ

N=22,4136m3/kmol

1

2

=

p

ϑ

2

1

Przeliczanie jednostek ciśnienia

p V = p V = const (dla m kg gazu)

760Tr=101325Pa

1

1

2

2

1Tr=133,322Pa

1Tr=1mmHg

Prawo Gay - Lussaca (przemiana izobaryczna) - objętość 1atm=101325Pa (atmosfera fizyczna)

gazu ogrzewanego lub ochładzanego przy stałym ciśnieniu 1at=98066,5Pa≈105Pa (atmosfera techniczna)

zmienia się wprost proporcjonalnie do zmiany temperatury 1bar=105Pa=750Tr

bezwzględnej

1at=1kG/cm2

p = const

ϑ

ϑ

V

V

1

2

=

=

const

lub

1

2

=

= const

T

T

T

T

1

2

1

2

MIESZANIE GAZÓW PRZY STAŁYM CIŚNIENIU

Prawo Charlesa (przemiana izochoryczna) - ciśnienie p=const

gazu ogrzewanego lub chłodzonego przy stałej objętości zmienia się wprost proporcjonalnie do zmiany temperatury 1

bezwzględnej

ϑ = const

3

p

2

1 = p2 = const

T

T

1

2

Równanie stanu gazu (równanie Clapeyrona)

m ⋅ c ⋅ t + m ⋅ c

⋅ t = m ⋅ c ⋅ t

1

p1

1

2

p 2

2

3

p3

3

p V

p V

1

1

2

2

=

= mR = const

m + m = m

T

T

1

2

3

1

2

•

⋅

+

⋅

=

dla 1kg masy gazu

g

c

g

c

c

1

p1

2

p 2

p 3

pϑ = RT

cp - ciepło właściwe masowe przy stałym ciśnieniu,

• dla m kg masy gazu

J/(kg⋅K), kJ/(kg⋅K)

pV = mRT

υ

- objętość właściwa gazu, m3/kg

V - objętość gazu, m3

m - masa gazu, kg

R - stała gazowa, J/(kg⋅K)

• stała gazowa:

B

R =

M

B - uniwersalna stała gazowa, B=8314,3J/(kmol⋅K) M - masa molowa gazu, kg/kmol

• Inna postać równania:

pΦ = BT

Φ = M

ϑ

pV = nTB

Φ - objętość molowa gazu, m3/kmol

n - ilość kmol gazu

Termodynamika ćw 1,2

MIESZANINY GAZÓW

Ciepło właściwe może być odniesione do:

Prawo Daltona - w danej objętości V mieszaniny gazów o

• jednostki masy gazu

temperaturze T i ciśnieniu p każdy ze składników cp , cv , J/(kg⋅K), k J/(kg⋅K)

mieszaniny m1, m2, ...,mn zachowując się tak jakby nie było

• jednostki objętości

innego gazu w tej objętości, czyli zajmuje całą objętość V, Cp , Cv , J/(um3⋅K) k J/( um3⋅K)

przyjmuje temperaturę T i ciśnienie picz.

• jednostki masy molowej

p = p

. . .

M

M

1 + p

2 +

+p

cz

cz

czk

Cp , Cv , J/(kmol⋅K), kJ/(kmol⋅K)

m = m

. . .

Zależność pomiędzy cp i cv (równanie Mayera): 1 + m 2 +

+mk

c − c = R

Skład mieszaniny gazów określają udziały masowe lub p

v

objętościowe składników.

M ⋅ c − M ⋅ c = M ⋅ R

•

p

v

Udział masowy

m

CM − CM = B

g

i

=

p

v

i

m

M - masa molowa

mi - masa i-tego składnika mieszaniny

B - uniwersalna stała gazowa, B ≅ 8314 J/(kmol⋅K) m - masa mieszaniny

Molowe ciepło właściwe

m = m

. . .

1

1 + m 2 +

+mk

M

C

= ⋅B ⋅(i + 2)

p

g

. . .

1

2

1 + g 2 +

+g =

k

• Udział objętościowy

1

CM =

⋅B ⋅i

V

v

r

i

=

2

i

V

i - liczba stopni swobody dla danego gazu

V

• dla gazu jednoatomowego i=3

i - objętość i-tego składnika mieszaniny

V - objętość mieszaniny

• dla gazu dwuatomowego i=5

V = V

. . .

• dla gazu trójatomowego i o większej liczbie atomów w 1 + V2 +

Vk

cząsteczce i=7

r

. . .

1

1 + r2 +

r =

k

Zależności

• Udział molowy

CM

n

c =

, J / (kg ⋅ K )

z

i

=

M

i

n

C

n

= , / ( ⋅

i - ilość moli i-tego składnika

c

J

kg K )

n - ilość moli mieszaniny

ρ

n = n

. . .

M

1 + n 2 +

+nk

C

C =

, J / (um3 ⋅ K )

z

. . .

1

1 + z2 +

z =

k

Φ

Wielkości zastępcze

M - masa molowa, kg/kmol

• Pozorna względna masa cząsteczkowa składnika ρ - gęstość, kg/m3

mieszaniny gazowej

Ciepło właściwe dla mieszaniny gazów

k

k

k

M

= ∑r M

⋅

= ∑ z M

⋅

c = ∑ g c

⋅ , J / (kg ⋅K)

m

i

i

i

i

m

i

i

i =1

i =1

i =1

Mi - masa molowa i-tego składnika mieszaniny

k

M

M

z

= ∑ ⋅ , / (

⋅

i - udział molowy i-tego składnika mieszaniny

C

z C

J

kmol K )

m

i

i

ri - udział objętościowy i-tego składnika mieszaniny i =1

M

k

g = r

i

= ∑ ⋅

3

, / (

⋅

i

i

C =

r C

⋅

J

um

K )

M

m

i

i

m

i =1

• Zastępcza stała gazowa mieszaniny

gi - udział masowy

k

B

zi - udział molowy

R

= ∑ g R

⋅ =

m

i

i

r

M

i - udział objętościowy

i =1

m

Wzory na obliczanie ilości ciepła

gi - udział masowy i-tego składnika

Q

n CM

= ⋅

⋅ T

∆

Ri - stała gazowa i-tego składnika

Q = m ⋅ c ⋅ T

∆

CIEPŁO WŁAŚCIWE

Q = V ⋅ C ⋅ T

∆

Ciepło właściwe oznacza ilość ciepła potrzebną do Q - ilość ciepła, J

ogrzania jednostki masy substancji o 1K.

W zale

CM - ciepło właściwe molowe, J/(kmol⋅K)

żności od warunków w jakich następuje ogrzewanie lub chłodzenie gazu rozróżniamy:

c - ciepło właściwe masowe, J/(kg⋅K)

• ciepło właściwe przy stałym ciśnieniu

C - ciepło właściwe objętościowe, J/(um3⋅K)

∆

c

T - różnica temperatury, K

p , J/(kg⋅K), k J/(kg⋅K)

• ciepło wła

ściwe przy stałej objętości

cv , J/(kg⋅K), k J/(kg⋅K)

Termodynamika ćw 1,2

GAZ PÓŁDOSKONAŁY

Gaz półdoskonały - czynnik termodynamiczny spełniający Mieszanina gazów półdoskonałych

równania gazu doskonałego, ale jego ciepło właściwe jest

zmienne i zależy od temperatury.

k

t

t

2

2

= ∑ ⋅

, / (

⋅ ), kJ / ( ⋅

W obliczeniach technicznych przemian gazów rzeczywistych c

g c

J

kg K

kg K )

m t

i

mi t

1

1

i =1

traktuje się je przeważnie jako gazy półdoskonałe.

k

t

t

C

2

= ∑ r ⋅C 2 , J / (um3 ⋅K), kJ / (um3 ⋅K) m

i

mi

Średnie ciepło właściwe

t

t

1

1

i =1

t

t

2

1

⋅ −

⋅

k

t

c

t

c

t

t

t

M

2

M

2

c 2

0

2

0

1

=

C

= ∑ z ⋅C

, J / (kmol ⋅ K ), kJ / (kmol ⋅ K ) m

i

mi

t

t

t

1

1

1

t −

t

i =1

2

1

t

gi - udział masowy

1 , t2 - temperatura początkowa i końcowa przemiany, 0C

z

ct1

i - udział molowy

0 -średnie ciepło właściwe gazu od temp. 00C do temp. t1, 0

r

C

i - udział objętościowy

ct20 - średnie ciepło właściwe gazu od temp. 00C do temp. t2, 0C

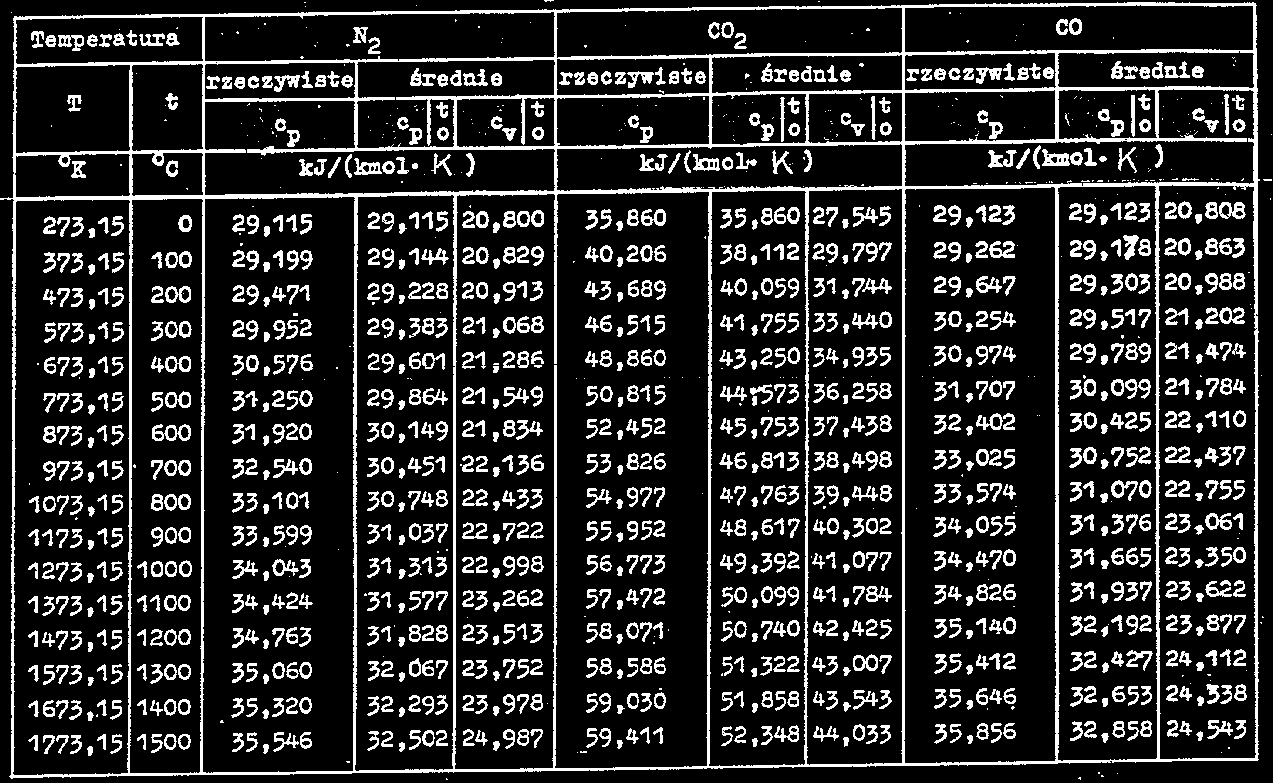
Ciepło właściwe gazów półdoskonałych