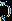
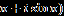
Arkusz nr 1.

1. Wykonać działania:

i

4

(

 )

3  1

( 

i

10 )

1 i

a) ( 2 + i) (3- 8 i )

b)

c)

5  i

4

1

(  i i

)

1

(  i)(2  i

3 )

d)

e) ( 2 + i) ( 2 - i)

i

2

a następnie znaleźć część rzeczywistą i urojoną otrzymanych liczb zespolonych.

2. Obliczyć:

a) i

b)  3  i

4

c)  4

d) ( 1+ 2i) 2

e) ( 2i ) 3

3. Rozwiązać w zbiorze liczb zespolonych równania: a) z 2 - z + 1 = 0

b) (i -3) z = 5 + i – z

c) (z+3i) (z 2 - 2i z + 3) = 0

d) ( z 2 + 1) (z 3 -2z 2 +5z) = 0

e) (z 4 - 16) (3i z +15) = 0

4. Na płaszczyźnie zespolonej narysować zbiory liczb z spełniających podane warunki: a) im [(1+2i)z – 3i]  0

b) re z < 2 oraz z  1

c) 2< z <4 oraz im z >0

d) 0<arg z <  oraz im z <1

e) z > 2 oraz 1<re z <2

5. Zapisać w postaci kartezjańskiej podane liczby: a) 2 (cos + i sin

b) 5 cos

c) 7 ( cos

6. Zapisać w postaci trygonometrycznej podane liczby zespolone: a) - 2 i

b) - 5

c) 1 – i

d) - i

7) Podane wielomiany rozłożyć na czynniki w dziedzinie zespolonej: a) W(z) = z2 - 16 i

b) W(z) = z2 + ( 1+ 4 i) z – (5 + i)

8) Napisać równanie kwadratowe, którego pierwiastkami są liczby a) z = 4 – i oraz z = 1 + 3 i

b) z = 1 – i oraz z = - 2 – 3 i

9) Napisać równanie okręgu o środku w punkcie z = 3 + 2 i oraz o promieniu 5.