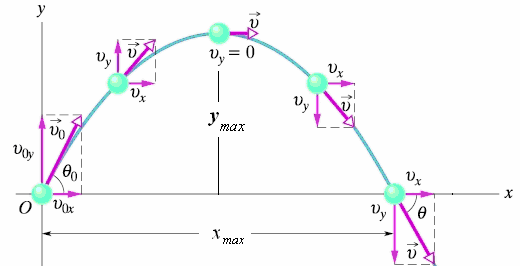
Rzut ukośny w polu grawitacyjnym rzut ukośny – ruch krzywoliniowy płaski (w płaszczyźnie xy) można rozłożyć na dwa niezależne ruchy składowe – jednostajny w kierunku x (poziomym) i jednostajnie zmienny w kierunku y (pionowym) prędkości:

υ = υ cos θ

x

0

0

(1 x)

υ = υ sin θ

0

0 − gt

y

(1 y)

położenia:

x = υ cos θ ⋅ t 0

0

(2 x)

1

2

y = υ sin θ ⋅ t − gt 0

0

(2 y)

2

należy wyznaczyć:

• maksymalną wysokość, na jaką wzniesie się ciało − ymax

• zasięg poziomy rzutu − xmax wysokość maksymalna – wysokość, przy której prędkość w kierunku pionowym = 0; korzystamy z (1 y) i obliczamy czas wznoszenia t’

υ sin θ

0 = υ sin θ

'

t

0

0

=

0

0 −

'

gt ⇒

g

podstawiamy t’ do (2 y): 2

υ sin θ

 υ sin θ 

y

= υ sin θ ⋅ 't 1

−

'

gt 2 = υ sin

0

0

1

θ ⋅

− g 0

0

=

max

0

0

2

0

0





g

2

g





2

υ sin2

2

θ

υ sin2

2

θ

υ sin2 θ

0

0

1

0

0

0

0

=

−

=

g

2

g

2 g

zasięg poziomy rzutu – odległość, przy której wysokość ciała ponownie = 0 (początkowa wysokość = 0);

korzystamy z (2 y) i obliczamy całkowity czas ruchu t”

1

2

0 = υ sin θ ⋅ "

t −

"

gt

0

0

2

/: t”

2 υ sin θ

1

υ sin θ =

"

gt

⇒ "t

0

0

=

0

0

2

g

t” = 2 t’ − czas wznoszenia stanowi połowę całkowitego czasu ruchu podstawiamy t” do (2 x): 2

2

2 υ sin θ

υ ⋅ 2sin θ cos θ

υ sin 2 θ

x

= υ cos θ ⋅ "

t

0

0

0

0

0

0

0

= υ cos θ ⋅

=

=

max

0

0

0

0

g

g

g