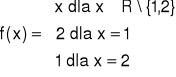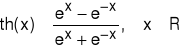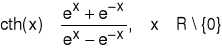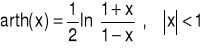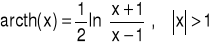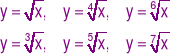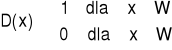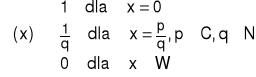I. zbiory i funkcje liczbowe

1.10 Funkcje odwrotne

Definicja (Funkcja różnowartościowa)

Funkcją f jest różnowartościowa na zbiorze A⊂D_f, jeżeli:

(1.10.1)

Definicja (Funkcja różnowartościowa); definicja równoważna

Funkcją f jest różnowartościowa na zbiorze A⊂D_f, jeżeli:

(1.10.2)

Uwaga:

Przy sprawdzaniu różnowartościowści funkcji wygodna jest definicja (1.10.2).

Funkcja różnowartościowa	Funkcja nieróżnowartościowa

Własność (Warunek wystarczający różnowartościowości funkcji)

Jeżeli funkcja jest rosnąca lub malejąca na zbiorze, to jest tam różnowartościowa.

Uwaga: Implikacja odwrotna nie jest prawdziwa. Na przykład funkcja jest różnowartościowa na R, ale nie jest rosnąca ani malejąca na tym zbiorze.

1.10 Funkcje odwrotne

Definicja (Funkcja odwrotna)

Funkcją
będzie różnowartościowa na dziedzinie. Funkcją odwrotną do f nazywamy funkcję f^-1:Y→X określoną przez warunek:

(1.10.3)

Własności:

• Funkcja odwrotna do funkcji rosnącej jest rosnąca.

• Funkcja odwrotna do funkcji malejącej jest malejąca.

Funkcja dana f	Funkcja odwrotna f^-1

Uwagi:

• Wykres funkcji odwrotnej x=f^-1(y) otrzymujemy z wykresu funkcji danej y=f(x) przekształcając go symetrycznie względem prostej y=x.

• Funkcje y=f(x) i y=f^-1(x) przedstawiamy w układzie XOY:

Funkcja dana w układzie XOY	y = f(x)
Funkcja odwrotna w układzie YOX	x = f^-1(y)
Funkcja odwrotna w układzie XOY	y = f^-1(x)

I. zbiory i funkcje liczbowe

1.11 Funkcje cyklometryczne

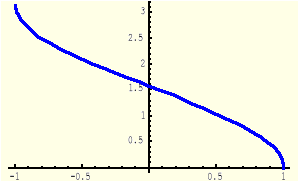
Definicja (Funkcja arcus sinus)

Funkcją arcus sinus, oznaczaną symbolem arcsin, nazywamy funkcję odwrotną do funkcji sinus obciętej do przedziału [-0.5π, 0.5π].

Dziedziną funkcji y=arcsin(x) jest przedział [-1,1]

Funkcja y=sinx	Funkcja y= arcsinx

Definicja (Funkcja arcus cosinus)

Funkcją arcus cosinus, oznaczaną symbolem arccos, nazywamy funkcję odwrotną do funkcji cosinus obciętej do przedziału [0,π].

Dziedziną funkcji y=arccos(x) jest przedział [-1,1]

Funkcja y=cosx	Funkcja y= arccosx

Tożsamości: Dla każdego x∈[-1,1]:

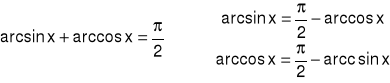
1.11 Funkcje cyklometryczne

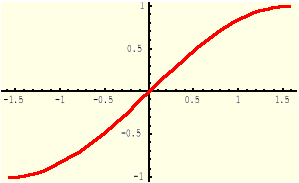
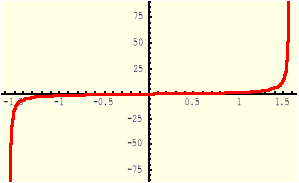
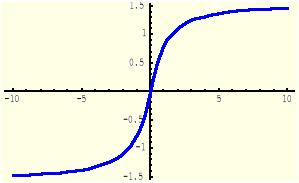
Definicja (Funkcja arcus tangens)

Funkcją arcus tangens, oznaczaną symbolem arctg, nazywamy funkcję odwrotną do funkcji tangens obciętej do przedziału [-0.5π, 0.5π].

Dziedziną funkcji y=arctg(x) jest zbiór R.

Funkcja y=tgx	Funkcja y= arctgx

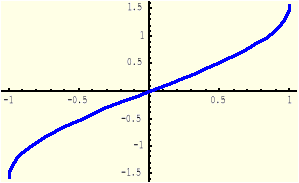
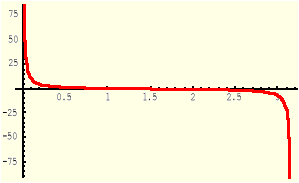
Definicja (Funkcja arcus kotangens)

Funkcją arcus kotangens, oznaczaną symbolem arcctg, nazywamy funkcję odwrotną do funkcji kotangens obciętej do przedziału [0,π].

Dziedziną funkcji y=arcctg(x) jest zbiór R.

Funkcja y=ctgx	Funkcja y= arcctgx

Tożsamości: Dla każdego x∈R:

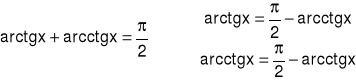
I. zbiory i funkcje liczbowe

1.12 Funkcje wykładnicza i logarytmiczna

Definicja (Funkcja wykładnicza o podstawie a)

Funkcją wykładniczą nazywamy funkcję postaci:

(1.12.1)

Definicja (Funkcja wykładnicza przy podstawie e)

Funkcją wykładniczą nazywamy funkcję postaci:

(1.12.2)

Definicja (Funkcja logarytmiczna - logarytm o podstawie a)

Funkcją logarytmiczą nazywamy funkcję postaci:

(1.12.3)

Definicja (Funkcja logarytmiczna - logarytm o podstawie a=10)

Funkcją logarytmiczą naturalną nazywamy funkcję postaci:

(1.12.4)

Definicja (Funkcja logarytmiczna - logarytm naturalny a=e)

Funkcją logarytmiczą naturalną nazywamy funkcję postaci:

(1.12.5)

Funkcje y = a^x, x∈R i y= loga(x) a>1, x∈R+	Funkcje y = a^x, x∈R i y= loga(x) 0<a<, x∈R+

I. zbiory i funkcje liczbowe

1.13 Funkcje hiperboliczne

Definicja (Funkcja sinus hiperboliczny)

Funkcją „sinus hiperboliczny”, oznaczaną symbolem sinh lub sh, nazywamy funkcję określoną wzorem:

(1.13.1)

Definicja (Funkcja cosinus hiperboliczny)

Funkcją „cosinus hiperboliczny”, oznaczaną symbolem cosh lub ch, nazywamy funkcję określoną wzorem:

(1.13.2)

Funkcja y = sh(x)	Funkcja y = ch(x)

Własności:

	(1.13.3)
	(1.13.4)
	(1.13.5)

1.13 Funkcje hiperboliczne

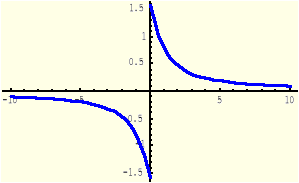
Definicja (Funkcja tangens hiperboliczny)

Funkcją „tangens hiperboliczny”, oznaczaną symbolem tgh lub th, nazywamy funkcję określoną wzorem:

(1.13.6)

Definicja (Funkcja cotangens hiperboliczny)

Funkcją „cotangens hiperboliczny”, oznaczaną symbolem ctgh lub cth, nazywamy funkcję określoną wzorem:

(1.13.7)

Funkcja y = th(x)	Funkcja y = cth(x)

Własności:

	(1.13.8)
	(1.13.9)
	(1.13.10)

1.13 Funkcje hiperboliczne

Definicja (Funkcja area sinus hiperboliczny)

Funkcją „area sinus hiperboliczny”, oznaczaną symbolem arsh, nazywamy funkcję określoną wzorem:

(1.13.11)

Definicja (Funkcja area cosinus hiperboliczny)

Funkcją „area cosinus hiperboliczny”, oznaczaną symbolem arch, nazywamy funkcję określoną wzorem:

(1.13.12)

Funkcja y = arsh(x)	Funkcja y = arch(x)

Własności:

Funkcje y=arsh(x) i y=arch(x) można wyrazić za pomocą logarytmu:

	(1.13.13)
	(1.13.14)

1.13 Funkcje hiperboliczne

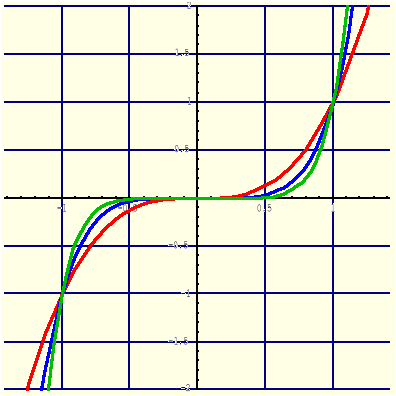
Definicja (Funkcja area tangens hiperboliczny)

Funkcją „area tangens hiperboliczny”, oznaczaną symbolem arth, nazywamy funkcję określoną wzorem:

(1.13.15)

Definicja (Funkcja area cotangens hiperboliczny)

Funkcją „area cotangens hiperboliczny”, oznaczaną symbolem arcth, nazywamy funkcję określoną wzorem:

(1.13.16)

Funkcja y = arth(x)	Funkcja y = arcth(x)

Własności:

Funkcje y=arth(x) i y=arcth(x) można wyrazić za pomocą logarytmu:

	(1.13.17)
	(1.13.18)

I. zbiory i funkcje liczbowe

1.14 Funkcje elementarne

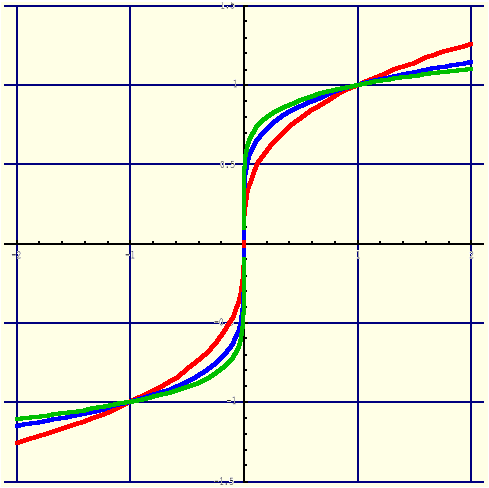
Definicja (Funkcja potęgowa)

Funkcję potęgową określamy wzorem:

(1.14.1)

Przykłady: Jeżeli n=0, to y=1. Jeżeli n=1, to y=x

Przykłady: Wykładnik n∈N\{0,1}.

n - parzyste (1.14.2)

n - nieparzyste (1.14.3)

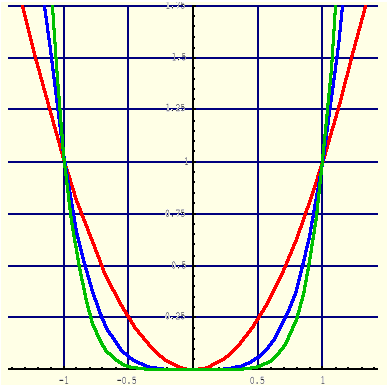
y = x^2, y = x^4, y = x^6	y = x^3, y = x^5, y = x^7

Funkcja	Dziedzina	Zbiór wartości	Wspólne punkty wykresów
y = 1 dla n=0	R	{1}	-
y = x dla n=1	R	R	-
y=x^n, n∈{2,4,6,...}	R	R+∪{0}	(-1,1); (0,0); (1,1)
y=x^n, n∈{3,5,7,...}	R	R	(-1,-1 ); (0,0); (1,1)

1.14 Funkcje elementarne

Przykłady: Wykładnik n∈C\{0}.

	|n| - parzyste (1.14.4)
	|n| - nieparzyste (1.14.5)

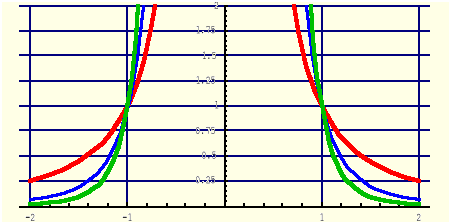
y = x^-2, y = x^-4, y = x^-6

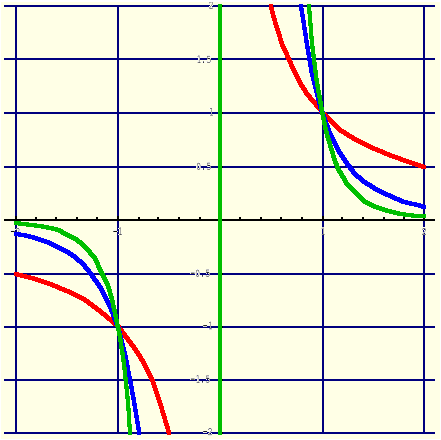
y = x^-3, y = x^-5, y = x^-7

Funkcja	Dziedzina	Zbiór wartości	Wspólne punkty wykresów
y=x^n, n∈{-2,-4,-6,...}	R\{0}	R+	(-1,1); (1,1)
y=x^n, n∈{-3,-5,-7,...}	R\{0}	R\{0}	(-1,-1); (1,1)

1.14 Funkcje elementarne

Przykłady: Wykładnik n=1/k, gdzie k=2, 4, 6.

(1.14.6)

Przykłady: Wykładnik n=1/k, gdzie k=3, 5, 7.

(1.14.7)

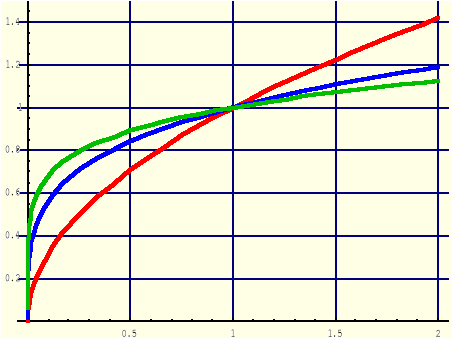
y = x^1/2, y = x^1/4, y = x^1/6

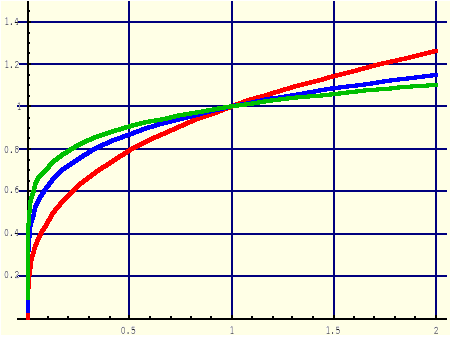
y = x^1/3, y = x^1/5, y = x^1/7

Funkcja	Dziedzina	Zbiór wartości	Wspólne punkty wykresów
y=x^1/k, k∈{2,4,6,...}	R+∪{0}	R+∪{0}	(0,0); (1,1)
y=x^1/k, k∈{3,5,7,...}	R+∪{0}	R+∪{0}	(0,0); (1,1)

1.14 Funkcje elementarne

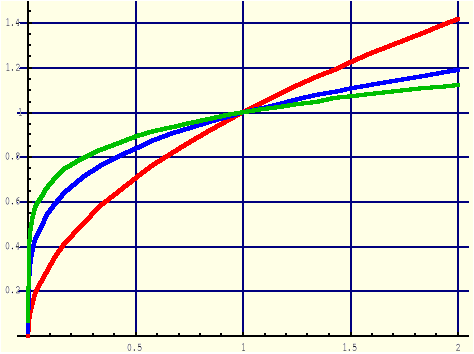
Definicja: (Funkcja pierwiastkowa)

(1.14.8)

Przykłady:

(1.14.9)

Funkcja	Dziedzina	Zbiór wartości	Wspólne punkty wykresów
n∈{2,4,6,...}	R+∪{0}	R+∪{0}	(0,0); (1,1)
n∈{3,5,7,...}	R	R	(-1,-1); (0,0); (1,1)

I. zbiory i funkcje liczbowe

1.15 Niektóre funkcje nielementarne

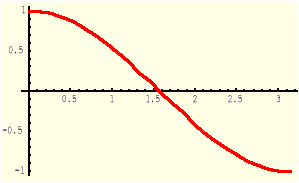
Definicja (Funkcja część całkowita)

Funkcją „część całkowita” nazywamy funkcję E: R→R określoną wzorem:

(1.15.1)

Uwaga: Część całkowita liczby x jest największą liczbą całkowitą nie większą niż x.

Funkcja część całkowita

Definicja (Funkcja mantysa)

Funkcją „mantysa” nazywamy funkcję M: R→R określoną wzorem:

(1.15.2)

Funkcja część całkowita

1.15 Niektóre funkcje nielementarne

Własności :

• Funkcja M(x) określona wzorem:

jest okresowa. • Funkcja E(x) spełnia warunek:	(1.15.3)
	(1.15.4)

Definicja (Funkcja signum)

Funkcją „signum” nazywamy funkcję sgn: R→R określoną wzorem:

(1.15.5)

Funkcja signum

1.15 Niektóre funkcje nielementarne

Definicja (Funkcja Dirichleta)

Funkcją Dirichleta nazywamy funkcję D: R→R określoną wzorem:

(1.15.6)

Funkcja Dirichleta

Definicja (Funkcja Riemanna)

Funkcją Riemanna nazywamy funkcję ℜ: R→R określoną wzorem:

(1.15.7)

Funkcja Riemanna

Funkcję „część całkowita” nazywa się również funkcją Einter (fr.), [czytaj: auntie]

Funkcję „mantysa” nazywa się również funkcją „piłoząbkową”.

Funkcja „signum” oznacza znak (łac.).

Peter Gustav Dirichlet (1805 - 1859), matematyk niemiecki.

Bernhard Georg Friedrich Riemann (1826 - 1866), matematyk niemiecki.

---