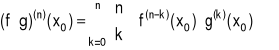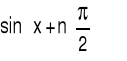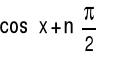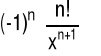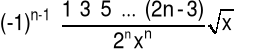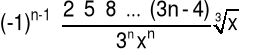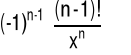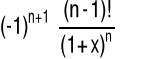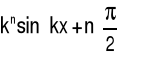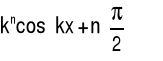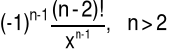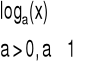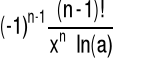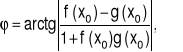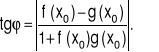4.6 Pochodne wyższych rzędów

Określenia

Definicja (Pochodna właściwa n-tego rzędu funkcji)

Pochodną właściwą n-tego rzędu funkcji f w punkcie x₀ określa się indukcyjnie następująco:

	(4.6.1)
	(4.6.2)
	(4.6.3)

Definicja (Funkcja n-krotnie różniczkowalna)

Funkcję, która ma pochodną właściwą n-tego rzędu na przedziale, nazywamy n-krotnie różniczkowalną na tym przedziale.

Uwaga:

Dla istnienia n-tej pochodnej funkcji f w punkcie x₀ konieczne jest istnienie pochodnej (n-1)-szej tej funkcji (także wszystkich poprzednich pochodnych) na pewnym otoczeniu punktu x_0.

Uwaga: Pochodne wyższych rzędów oznacza się symbolami:

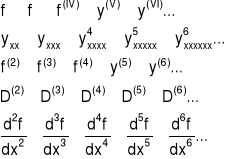
4.6 Pochodne wyższych rzędów

Pochodna n-ta iloczynu dwóch funkcji

Twierdzenie (Wzór Leibnitza)

Jeżeli funkcje f i g mają pochodne właściwe n-tego rzędu w punkcie x₀, to

(4.6.4)

Dla n=1

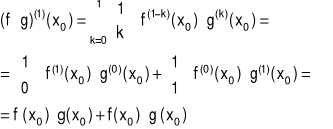
Dla n=2

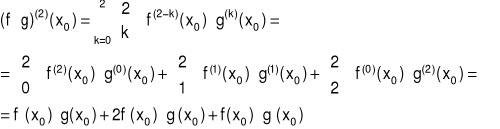
Uwaga: Silnia

Uwaga: Symbol Newtona i jego własności

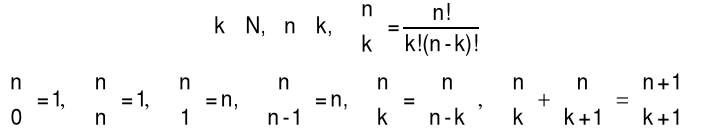
4.6 Pochodne wyższych rzędów

Pochodne rzędu n niektórych funkcji

Tablica

Funkcja f(x)	Pochodna f^(n)(x)
sin(x)		(4.6.5)
cos(x)		(4.6.6)
e^x	e^x	(4.6.7)
a^x	a^x(lna)^n	(4.6.8)
x^n	n!	(4.6.9)
		(4.6.10)
		(4.6.11)
		(4.6.12)
ln(x), x>0		(4.6.13)
ln(x+1), x>-1		(4.6.14)

4.6 Pochodne wyższych rzędów

Pochodne rzędu n niektórych funkcji

Tablica c.d.

Funkcja f(x)	Pochodna f^(n)(x)
sin(kx)		(4.6.15)
cos(kx)		(4.6.16)
e^kx	k^ne^kx	(4.6.17)
a^kx	a^kx(k⋅lna)^n	(4.6.18)
x^m	m(m-1)(m-2)⋅…⋅(m-n+1)x^m-n	(4.6.19)
xe^x	(x+n)e^x	(4.6.20)
xln(x)		(4.6.21)
		(4.6.22)
sinh(x)	sinh(x) dla n parzystego	(4.6.23)
			cosh(x) dla n nieparzystego
	cosh(x)		cosh(x) dla n parzystego	(4.6.24)
			sinh(x) dla n nieparzystego

4.6 Pochodne wyższych rzędów

Przykład 1 Obliczyć drugą pochodną funkcji y=arcsin(x)

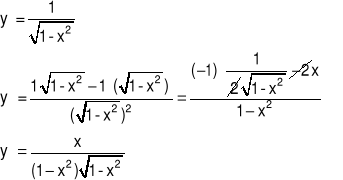
Przykład 2 Obliczyć drugą pochodną funkcji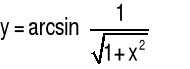

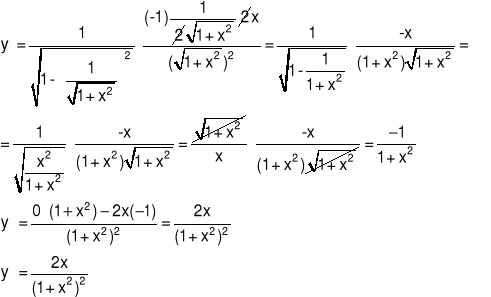
4.6 Pochodne wyższych rzędów

Przykład 3 Która pochodna funkcji y=2x⁶-x³+2x-3 jest równa 0?

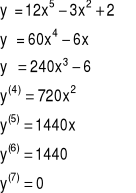
Przykład 4 Obliczyć czwartą pochodną funkcji y=x²sin(2x) w

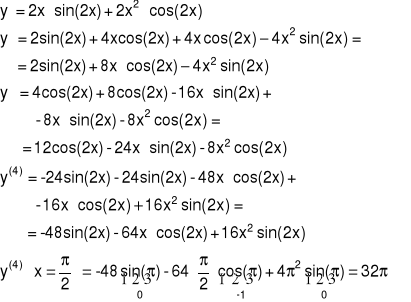
4.6 Pochodne wyższych rzędów

Wzór Leibniza

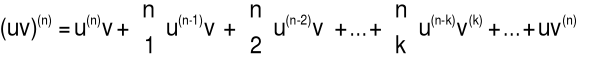
Przykład 1 Obliczyć czwartą pochodną funkcji y = x⁵cos(x)

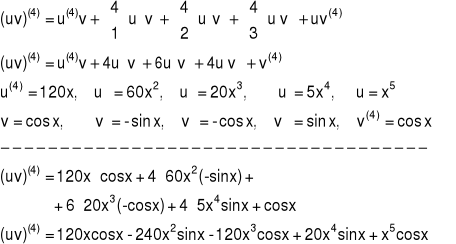
Przykład 2 Obliczyć czwartą pochodną funkcji y = sin(x)cos(x)

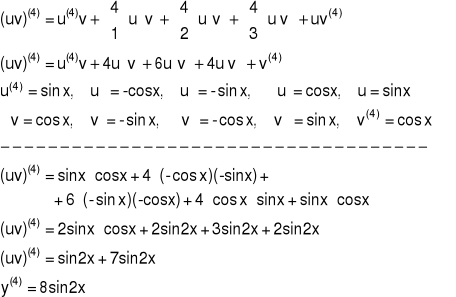
4.6 Pochodne wyższych rzędów

Wzór Leibniza

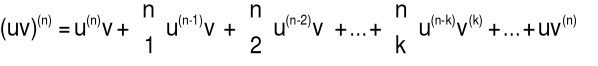
Przykład 3 Obliczyć piątą pochodną funkcji y = e^xsin(x)

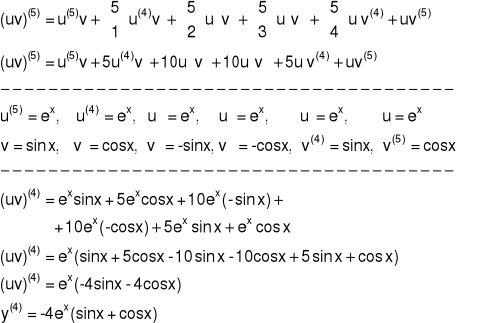
Przykład 4 Obliczyć piątą pochodną funkcji y = sin(x)cos(x)

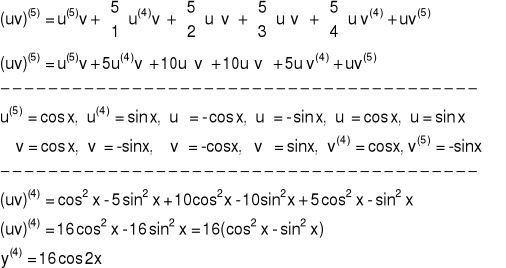
4.7 Pochodna a styczna do wykresu funkcji

Styczna i normalna do wykresu funkcji

Definicja (Styczna do wykresu funkcji)

Niech x₀∈R i niech funkcja ciągła f będzie określona przynajmniej na otoczeniu O(x₀).

Prosta jest styczną do wykresu funkcji f w punkcie (x₀,f(x₀)), jeżeli jest granicznym położeniem siecznych wykresu funkcji f przechodzących przez punkty (x₀,f(x₀)) i (x,f(x)), gdy x→x₀.

Twierdzenie (Równanie stycznej do wykresu funkcji)

Równanie stycznej do wykresu funkcji f w punkcie (x₀,y₀) ma postać

(4.7.1)

Interpretacja geometryczna

Położenie siecznych i stycznej w punkcie (x₀,f(x₀))

Twierdzenie (Równanie normalnej do wykresu funkcji)

Równanie normalnej do wykresu funkcji f w punkcie (x₀,y₀) ma postać

(4.7.2)

4.7 Pochodna a styczna do wykresu funkcji

Kąt przecięcia wykresów funkcji

Definicja (Kąt przecięcia wykresów dwóch funkcji)

Niech wykresy funkcji f oraz g mają wspólny punkt (x₀,y₀) oraz obie funkcje mają pochodne właściwe w punkcie x₀. Kątem przecięcia wykresów funkcji f i g nazywamy kąt ostry ϕ między stycznymi do wykresów tych funkcji w punkcie ich przecięcia.

Twierdzenie (O mierze kąta między wykresami funkcji)

Miara kąta przecięcia wykresów funkcji f i g wyraża się wzorem:

(4.7.3)

gdzie x₀ jest rzędną punktu przecięcia wykresów.

Uwaga: Jeżeli f′(x₀)g′(x₀) = -1, to przyjmuje się, że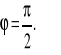

Uwaga: Kąt ϕ można wyznaczyć mając

Interpretacja geometryczna

Kąt ϕ między stycznymi w punkcie (x₀,y₀)

4.7 Pochodna a styczna do wykresu funkcji

Styczna i normalna do wykresu funkcji

Przykład 1 Znaleźć równanie stycznej i normalnej do wykresu funkcji f(x) = x² - 4x + 5 w punkcie (3,2).

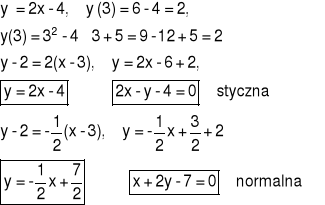
Przykład 2 Znaleźć równanie stycznej i normalnej do wykresu funkcji
w punkcie (-1, f(-1)).

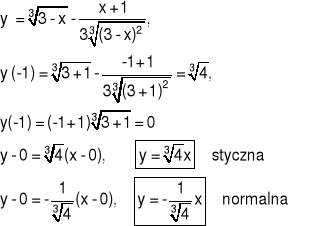
4.7 Pochodna a styczna do wykresu funkcji

Kąt przecięcia wykresów funkcji

Przykład 1 Znaleźć kąt, pod którym przecinają się wykresy funkcji

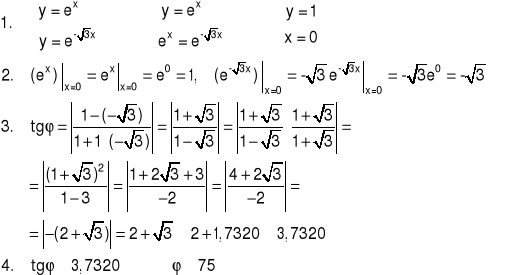
Interpretacja geometryczna

Gottfried Wilhelm Leibniz (1646 - 1716) - matematyk niemiecki.

---