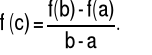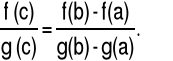V. twierdzenia o funkcjach z pochodnymi

5.1 Twierdzenia o wartości średniej

Twierdzenie (Rolle'a)

Jeżeli funkcja f spełnia warunki:

jest ciągła na [a,b],	(5.1.1)
ma pochodną właściwą lub niewłaściwą na (a,b),	(5.1.2)
f(a) = f(b),	(5.1.3)

to istnieje punkt c∈(a,b) taki, że

f′(c) = 0.

(5.1.4)

Interpretacja geometryczna

Na wykresie funkcji ciągłej na [a,b], mającej pochodną wewnątrz tego przedziału i przyjmującej równe wartości na jego końcach, istnieje punkt, w którym styczna jest pozioma.

5.1 Twierdzenia o wartości średniej

Twierdzenie (Lagrange'a)

Jeżeli funkcja f spełnia warunki:

jest ciągła na [a,b],	(5.1.5)
ma pochodną właściwą lub niewłaściwą na (a,b),	(5.1.6)

to istnieje punkt c∈(a,b), taki, że

(5.1.7)

Interpretacja geometryczna

Na wykresie funkcji ciągłej na [a,b], mającej pochodną wewnątrz tego przedziału istnieje punkt, w którym styczna do wykresu jest równoległa siecznej łączącej jego końce.

5.1 Twierdzenia o wartości średniej

Twierdzenie (Cauchy'ego)

Jeżeli funkcje f oraz g spełniają warunki:

są ciągłe na [a,b],	(5.1.8)
mają pochodne właściwe lub niewłaściwe na (a,b),	(5.1.9)
g′(x) ≠ 0 dla każdego x∈(a,b),	(5.1.10)

to istnieje punkt c∈(a,b), taki, że

(5.1.11)

Interpretacja geometryczna

Na wykresie funkcji ciągłej na [a,b], mającej pochodną wewnątrz tego przedziału istnieje punkt, w którym styczna do wykresu jest równoległa siecznej łączącej jego końce.

V. twierdzenia o funkcjach z pochodnymi

5.2 Monotoniczność funkcji

Twierdzenie

(Warunki wystarczające monotoniczności funkcji)

Niech A oznacza dowolny przedział. Jeżeli dla każdego x∈A funkcja f spełnia warunek:

to jest stała na A;	(5.2.1)
to jest rosnąca na A;	(5.2.2)
to jest niemalejąca na A;	(5.2.3)
to jest malejąca na A;	(5.2.4)
to jest nierosnąca na A;	(5.2.5)

Twierdzenie (O tożsamościach)

Niech funkcje f oraz g będą określone na przedziale A⊂R i niech x₀∈A. Wtedy, jeżeli spełnione są warunki:

f(x0) = g(x0);	(5.2.6)
f′(x) = g′(x) dla każdego x∈A,	(5.2.7)
to f(x) ≡ g(x) na A.	(5.2.8)

Twierdzenie (O nierównościach)

Niech funkcje f oraz g będą określone na przedziale A⊂R i niech x₀∈A. Wtedy, jeżeli spełnione są warunki:

	(5.2.9)
dla każdego x>x0,	(5.2.10)
to dla każdego x>x0.	(5.2.11)

5.2 Monotoniczność funkcji

Przykład 1 Zbadać monotoniczność funkcji:

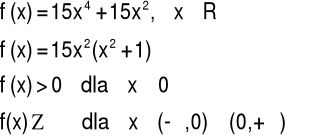
Przykład 2 Zbadać monotoniczność funkcji:

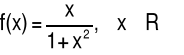
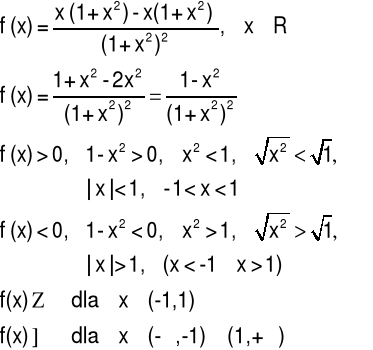
5.2 Monotoniczność funkcji

Przykład 3 Zbadać monotoniczność funkcji:

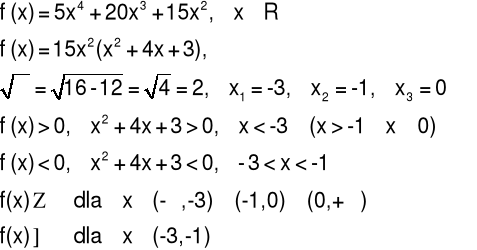
Przykład 4 Zbadać monotoniczność funkcji:

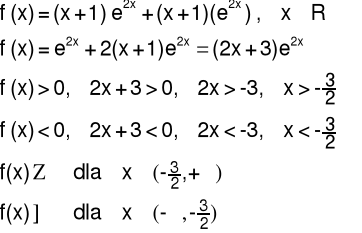
5.2 Monotoniczność funkcji

Przykład 5 Zbadać monotoniczność funkcji:

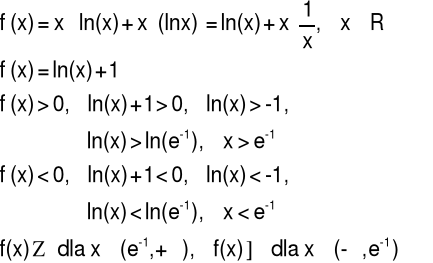
Przykład 6 Zbadać monotoniczność funkcji:

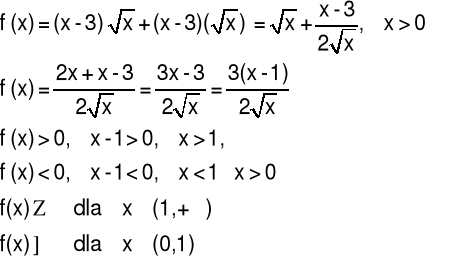
5.2 Monotoniczność funkcji

Przykład 7 Zbadać monotoniczność funkcji:

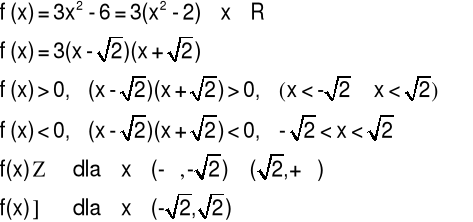
Przykład 8 Zbadać monotoniczność funkcji:

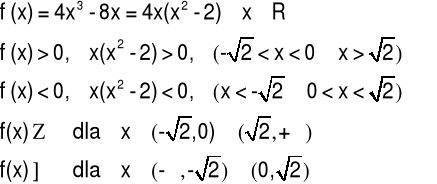
5.1 Twierdzenia o wartości średniej

Przykład 1 Sprawdzić, czy funkcja f(x) = x(x²-1) spełnia założenia twierdzenia Rolle'a na przedziale [-1,1].

Rozwiązanie:

1. Funkcja f(x) = x(x²-1) jest ciągła na przedziale [-1,1], ponieważ jest wielomianem.

2. Funkcja f(x) = x(x²-1) ma pochodną właściwą na przedziale [-1,1], ponieważ jest wielomianem.

3. f(-1)=(-1)[(-1)²-1]=0, f(1)=1(1²-1)=0 Zatem f(-1)=f(1)

4. Wniosek:

5.1 Twierdzenia o wartości średniej

Przykład 2 Sprawdzić, czy funkcja
spełnia założenia twierdzenia Rolle'a na przedziale [-1,1].

Rozwiązanie:

1. Funkcja f(x) = x(x²-1) jest ciągła na przedziale [-1,1], ponieważ jest wielomianem.

2. Funkcja f(x) = x(x²-1) ma pochodną właściwą na przedziale [-1,1], ponieważ jest wielomianem.

3. f(-1) = (-1)[(-1)²-1] = 0, f(1) = 1(1²-1) = 0, zatem f(-1)=f(1)

Michael Rolle (1652 - 1719), matematyk francuski.

Joseph Louis de Lagrange (1736 - 1813), matematyk i astronom francuski.

Augustin Louis Cauchy (1789 - 1857), matematyk francuski.

---