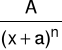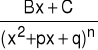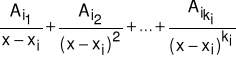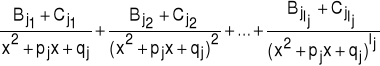7.8 Całkowanie funkcji wymiernych
Funkcja wymierna i ułamki proste
Definicja (Funkcja wymierna właściwa)
Funkcją wymierną:
|
(7.8.1) |
nazywamy właściwą, gdy stopień wielomianu w liczniku jest mniejszy od stopnia wielomianu w mianowniku, tzn. n<m.
Uwaga: Każdą funkcję wymierną niewłaściwą (n≥m) można przedstawić w postaci sumy wielomianu i funkcji wymiernej właściwej.
Definicja (Ułamek prosty 1-go rodzaju)
Funkcją wymierną właściwą postaci:
|
(7.8.2) |
gdzie n∈N oraz a,A∈R, nazywamy ułamkiem prostym pierwszego rodzaju.
Definicja (Ułamek prosty 2-go rodzaju)
Funkcją wymierną właściwą postaci:
|
(7.8.3) |
gdzie n∈N oraz p, q, B, C∈R przy czym Δ = p2 - 4q < 0 nazywamy ułamkiem prostym drugiego rodzaju.
7.8 Całkowanie funkcji wymiernych
Rozkład funkcji wymiernej na ułamki proste
Twierdzenie (O rozkładzie funkcji wymiernej na ułamki proste)
Każda funkcja wymierna właściwa rzeczywista jest sumą ułamków prostych. Przedstawienie to jest jednoznaczne.
Funkcja wymierna właściwa:
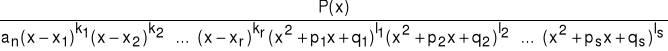
...(7.8.4)
jest sumą k1+k2+...kr ułamków prostych pierwszego rodzaju oraz l1+l2+...+ls ułamków prostych drugiego rodzaju, gdzie
• czynnikowi ![]()
odpowiada suma ki ułamków prostych pierwszego rodzaju postaci:
|
(7.8.5) |
![]()
• a czynnikowi ![]()
odpowiada suma lj ułamków prostych drugiego rodzaju postaci:
|
(7.8.6) |
![]()
7.8 Całkowanie funkcji wymiernych
Przykłady rozkładu funkcji wymiernych na ułamki proste
(bez wyznaczania niewiadomych współczynników)
Przykład 1

Przykład 2
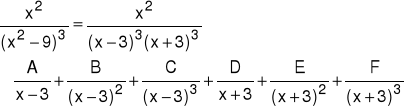
Przykład 3
![]()
Przykład 4

Przykład 5
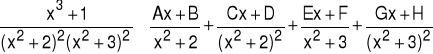
Przykład 6

7.8 Całkowanie funkcji wymiernych
Przykład rozkładu funkcji wymiernej na ułamki proste
(z wyznaczaniem niewiadomych współczynników)
Przykład 1 Przedstawić funkcję wymierną:
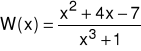
w postaci sumy ułamków prostych.
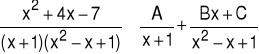
![]()
![]()
![]()
Stosując twierdzenie o równości wielomianów mamy układ:
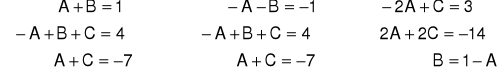
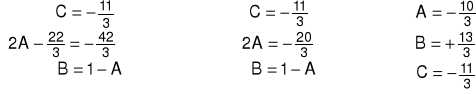
Zatem szukany rozkład ma postać:
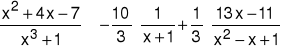
7.8 Całkowanie funkcji wymiernych
Algorytm całkowania funkcji wymiernych
![]()
Krok: |
Operacja: |
Twierdzenia: |
Zapis dowolnej funkcji wymiernej w postaci sumy wielomianu i funkcji wymiernej właściwej. |
Tw. o dzieleniu wielomianów. |
|
Rozkład mianownika funkcji wymiernej właściwej na czynniki liniowe i kwadratowe nierozkładalne. |
Tw. o grupowaniu wyrazów. Tw. o pierwiastkach wielomianu. Tw. o podzielności wielomianów. |
|
Zapis rozkładu funkcji wymiernej właściwej na ułamki proste pierwszego i drugiego rodzaju. |
Tw. o rozkładzie funkcji wymiernej. |
|
Znalezienie nieznanych współczynników tego rozkładu oraz podanie jego ostatecznej postaci. |
Tw. o równości wielomianów. Tw. o rozwiązywaniu układu równań liniowych metodą przeciwnych współczynników. |
|
Obliczenie całek nieoznaczonych poszczególnych składników rozkładu funkcji wymiernej (tj. wielomianu oraz ułamków prostych). |
Tw. o całce nieoznaczonej. Podstawowe wzory całkowania. |
7.8 Całkowanie funkcji wymiernych
Przykłady całkowania funkcji wymiernych
Przykład 1 Obliczyć całkę :
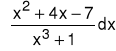
Rozwiązanie:
Rozkład: 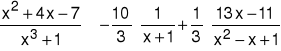
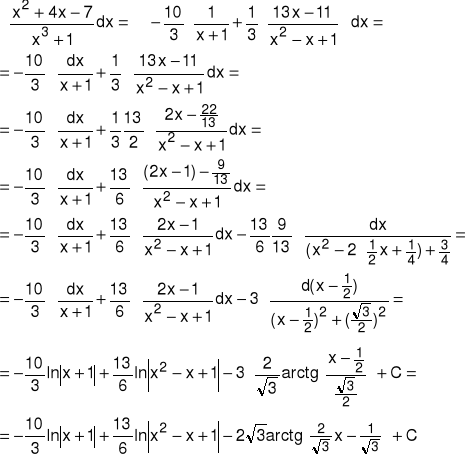
Wyszukiwarka
Podobne podstrony:
5Analiza-6C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-3, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-4, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-2C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7E, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-1B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
więcej podobnych podstron