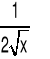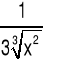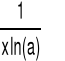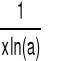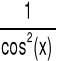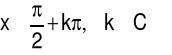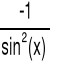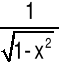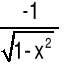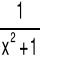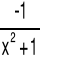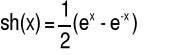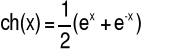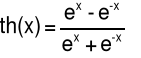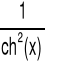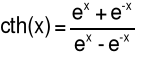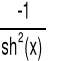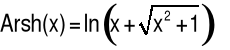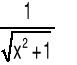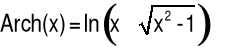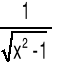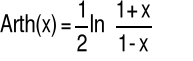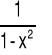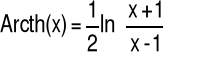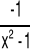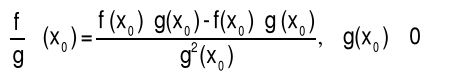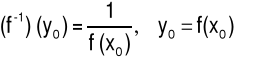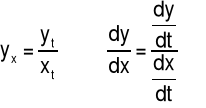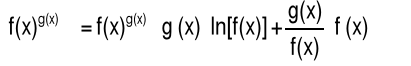4.3 Pochodne funkcji elementarnych
Wzory pochodnych funkcji elementarnych
f(x) |
f′(x) |
Uwagi |
C |
0 |
|
xn |
nxn-1 |
n∈N, n≥2, x∈R |
xα |
αxα-1 |
α∈R, x∈R |
x |
1 |
x∈R |
x2 |
2x |
x∈R |
x3 |
3x2 |
x∈R |
|
|
x∈R+ |
|
|
x∈ R\{0} |
|
|
x∈R\{0}, a≠0 |
|
|
x∈R\{0} |
ax |
ax ⋅ln(a) |
x∈R, a∈R+\{1} |
ex |
ex |
x∈R |
loga|x| |
|
a∈R+\{1}, x∈R\{0} |
loga(x) |
|
a∈R+\{1}, x∈R+ |
ln|x| |
|
x∈R\{0} |
ln(x) |
|
x∈R+ |
4.3 Pochodne funkcji elementarnych
Wzory pochodnych funkcji trygonometrycznych
f(x) |
f′(x) |
Uwagi |
sin(x) |
cos(x) |
x∈R |
cos(x) |
-sin(x) |
x∈R |
tg(x) |
|
|
ctg(x) |
|
|
arcsin(x) |
|
x∈(-1,1) |
arccos(x) |
|
x∈(-1,1) |
arctg(x) |
|
x∈R |
arcctg(x) |
|
x∈R |
|
ch(x) |
x∈R |
|
sh(x) |
x∈R |
|
|
x∈R |
|
|
x∈(-∞,0)∪(0,+∞) |
|
|
x∈R |
|
|
x≥1 |
|
|
|x|<1 |
|
|
|x|>1 |
4.4 Twierdzenia o pochodnych funkcji
Pochodne jednostronne funkcji w punkcie
Definicje (Pochodna właściwa funkcji w punkcie x0)
Niech x0∈R i niech funkcja f będzie określona przynajmniej na otoczeniu ![]()
. Pochodną lewostronną właściwą funkcji f w punkcie x0 nazywamy granicę właściwą:
|
(4.4.1) |
Niech x0∈R i niech funkcja f będzie określona przynajmniej na otoczeniu ![]()
. Pochodną prawostronną właściwą funkcji f w punkcie x0 nazywamy granicę właściwą:
|
(4.4.2) |
Twierdzenie (Warunek konieczny i dostateczny istnienia pochodnej)
Funkcja f ma pochodną w punkcie x0 wtedy i tylko wtedy, gdy
|
(4.4.3) |
Definicje (Pochodna funkcji w przedziale, funkcja różniczkowalna)
Funkcja f ma pochodną w przedziale |
jeżeli ma pochodną |
(a,b) , |
w każdym punkcie tego przedziału |
[a,b) , |
w (a,b) i prawostronną pochodną w a |
(a,b] , |
w (a,b) i lewostronną pochodną w b |
[a,b] , |
w (a,b), prawostronną pochodną w a i lewostronną pochodną w b |
(-∞,b] , |
w (-∞,b) i lewostronną pochodną w b |
[a,+∞) , |
w (a,+∞) i prawostronną pochodną w a |
4.4 Twierdzenia o pochodnych funkcji
Twierdzenia (O arytmetyce pochodnych funkcji)
Jeżeli funkcje f i g mają pochodne właściwe w punkcie x0, to
|
(4.4.4) |
|
(4.4.5) |
|
(4.4.6) |
|
(4.4.7) |
|
(4.4.8) |
Twierdzenie (O pochodnej funkcji złożonej)
Jeżeli:
1. funkcja f ma pochodną właściwą w punkcie x0
2. funkcja g ma pochodną właściwą w punkcie f(x0), to
|
(4.4.9) |
Twierdzenie (O pochodnej funkcji odwrotnej)
Jeżeli funkcja f spełnia warunki:
1. jest ciągła na otoczeniu O(x0),
2. jest ściśle monotoniczna na otonczeniu O(x0),
3. ma pochodną właściwą f′(x0) ≠ 0, to
|
(4.4.10) |
Uwaga:
Powyższe wzory są prawdziwe dla pochodnych jednostronnych.
4.4 Twierdzenia o pochodnych funkcji
Twierdzenie (O pochodnych funkcji elementarnych)
Pochodne funkcji elementarnych są funkcjami elementarnymi.
Twierdzenie (O pochodnej funkcji niejawnej)
Jeśli funkcja różniczkowalna y=f(x) jest przedstawiona równaniem F(x,y)=0, to pochodna tej funkcji y′=f′(x) może być wyznaczona z równania:
|
(4.4.11) |
Twierdzenie (O pochodnej funkcji parametrycznej)
Jeśli funkcja y=f(x) jest przedstawiona równaniami parametrycznymi:
|
(4.4.12) |
gdzie x(t) i y(t) są funkcjami różniczkowalnymi i x′(t)≠0, to pochodna y′=f′(x) wyraża się wzorem:
|
(4.4.13) |
Twierdzenie (O pochodnej funkcji potęgowo-wykładniczej)
Pochodną funkcji potęgowo-wykładniczej y=[f(x)]g(x), gdzie funkcje f oraz g są różniczkowalne przedstawia wzór:
|
(4.4.14) |
Wyszukiwarka
Podobne podstrony:
5Analiza-7B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-3, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-4, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-2C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7E, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-1B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
więcej podobnych podstron