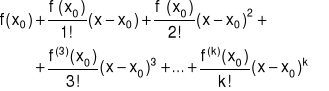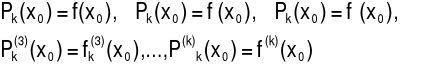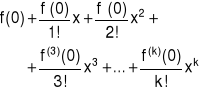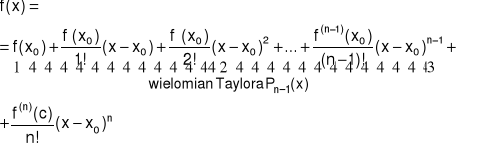V. twierdzenia o funkcjach z pochodnymi

5.5 Rozwinięcie Taylora funkcji

Definicja (Wielomian Taylora)

Niech funkcja f ma w punkcie x₀ pochodną właściwą k-tego rzędu dla k∈N∪{0}. Wielomian:

(5.5.1)

nazywamy wielomianem Taylora rzędu k funkcji f w punkcie x₀ i oznaczamy symbolem P_k(x).

Uwaga:

Wielomian P(x) jest jedynym wielomianem stopnia k, który spełnia warunki:

(5.5.2)

Definicja (Wielomian Maclaurina)

Wielomian Taylora dla x₀=0 jest wielomianem Maclaurina, który ma postać

(5.5.3)

5.5 Rozwinięcie Taylora funkcji

Twierdzenie (Wzór Taylora z resztą Lagrange'a)

Jeżeli funkcja f ma:

ciągłą pochodną rzędu n-1 na przedziale [x0,x]	(5.5.4)
pochodną właściwą f^(n) na przedziale (x0,x)	(5.5.5)

to istnieje punkt c∈(x₀,x) taki, że

… (5.5.6)

Uwaga:

Równość występująca w tezie twierdzenia nazywamy wzorem Taylora.

Definicja (Reszta Lagrange'a)

Wyrażenie:

(5.5.7)

nazywamy n-tą resztą Lagrange'a.

Uwaga:

Resztę Lagrange'a można zapisać w postaci:

(5.5.8)

gdzie 0<Θ<1 oraz Δx=x-x₀.

5.5 Rozwinięcie Taylora funkcji

Rozwinięcie Maclaurina w otoczeniu zera

Przykład 1

Obliczyć przybliżoną wartość liczby e z dokładnością do 0,001.

Rozwiązanie:

1. Pochodne funkcji f(x)=e^x:

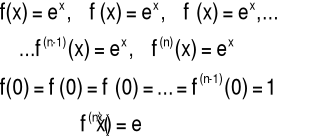
2. W każdym przedziale o końcach skończonych funkcja e^x oraz jej [pochodne są ograniczone. To oznacza, że R_n→0, gdy x→∞ i funkcja e^x ma rozwinięcie Maclaurina.

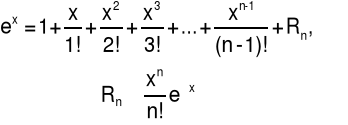
3. Dla x=1 otrzymujemy:

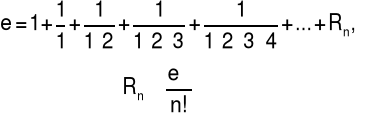
Brook Taylor (1685 - 1731), matematyk angielski.

Colin Maclaurin (1698 - 1746), matematyk szkocki.

Joseph Louis de Lagrange (1736 - 1813), matematyk i astronom francuski.

---