IV. pochodne funkcji

4.1 Iloraz różnicowy funkcji

Określenie

Definicja (Iloraz różnicowy)

Niech x₀∈R oraz niech funkcja f będzie określona przynajmniej na otoczeniu O(x₀,r), gdzie r>0.

Ilorazem różnicowym funkcji f w punkcie x₀ odpowiadającym przyrostowi Δx, gdzie 0<|Δx|<r, zmiennej niezależnej nazywamy liczbę:

(4.1.1)

Interpretacja ilorazu geometryczna

Iloraz różnicowy funkcji f=f(x)

4.1 Iloraz różnicowy funkcji

Interpretacje ilorazu różnicowego

• Interpretacja geometryczna

♦ Iloraz różnicowy jest tangensem kąta nachylenia siecznej wykresu funkcji f, przechodzącej przez punkty A(x₀, f(x₀)) oraz B(x₀+Δx, f(x₀+Δx)), do dodatniej części osi Ox:

(4.1.2)

• Interpretacje fizyczne

♦ Niech S(t) oznacza drogę na osi punktu materialnego w chwili t. Iloraz

(4.1.3)

oznacza średnią prędkość poruszającego się punktu w odstępie czasu Δt.

♦ Niech v(t) oznacza prędkość punktu materialnego w chwili t. Iloraz

(4.1.4)

oznacza średnie przyspieszenie poruszającego się punktu w odstępie czasu Δt.

♦ Niech Q(t) oznacza ilość ładunków elektrycznych, jaka w przedziale czasu Δt przepłynęła przez ustalony przekrój przewodnika. Iloraz:

(4.1.5)

oznacza średnie natężenie prądu w odstępie czasu Δt.

4.1 Iloraz różnicowy funkcji

Przykład 1

Obliczyć iloraz różnicowy dla funkcji f(x)=x² w punkcie x₀=-1 odpowiadający przyrostowi Δx=0,1.

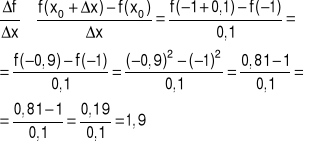
Przykład 2

Obliczyć iloraz różnicowy dla funkcji f(x) = log₂(x) w punkcie x₀ =1 odpowiadający przyrostowi Δx = -0,2.

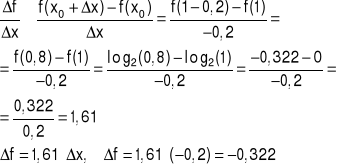
Uwaga:

Wartość logarytmu z 0,8 o podstawie 2 w programie Mathcad:

log(0.8,2) = -0.322

4.1 Iloraz różnicowy funkcji

Przykład 3

Obliczyć iloraz różnicowy dla funkcji f(x) = ln(x) w punkcie x₀=1 odpowiadający przyrostowi Δx = -0,2.

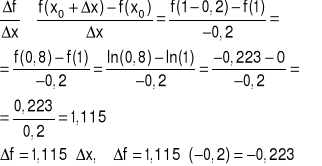
Uwaga: Wartość logarytmu naturalnego z 0,8 w programie Mathcad

log(0.8,e) = -0.223, ln(x) ≡ log_e(x)

Przykład 4

Obliczyć iloraz różnicowy dla funkcji f(x)=lg(x) w punkcie x₀=1 odpowiadający przyrostowi Δx=-0,2.

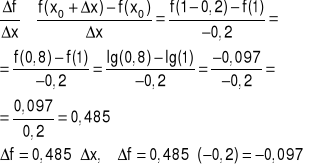
Uwaga: Wartość logarytmu dziesiętnego z 0,8 w programie Mathcad

log(0.8,10) = -0.087, log(x) ≡ lg(x)

4.1 Iloraz różnicowy funkcji

Wykresy funkcji logarytmicznych

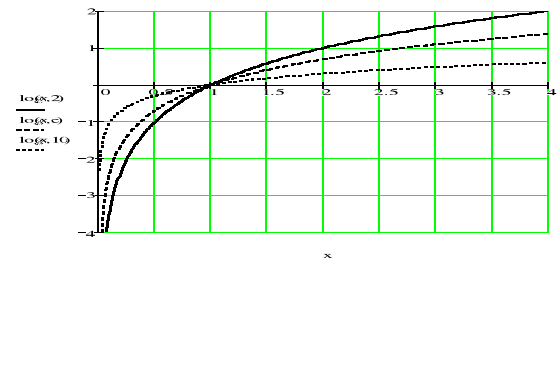
Wykresy funkcji y=log₂(x), y=ln(x), y=lg(x) dla 0<x<4

Wykresy funkcji y=log₂(x), y=ln(x), y=lg(x) dla 0,4<x<1

4.2 Pochodna właściwa funkcji funkcji

Definicje (Pochodna właściwa funkcji w punkcie x₀)

Niech x₀∈R i niech funkcja f będzie określona przynajmniej na otoczeniu O(x₀). Pochodną właściwą funkcji f w punkcie x₀ nazywamy granicę właściwą:

(4.2.1)

Pochodna funkcji f w punkcie x₀ jest granicą ilorazu różnicowego Δf/Δx przy x_n→x₀. Zatem:

(4.2.2)

Pochodna funkcji f w punkcie x₀ jest granicą ilorazu różnicowego Δf/Δx przy Δx→0, gdy x_n = x₀+Δx. Mamy zatem:

(4.2.3)

Twierdzenie (Warunek konieczny istnienia pochodnej właściwej funkcji)

Jeżeli funkcja ma pochodna właściwą w punkcie, to jest ciągła w tym punkcie.

Uwaga: Implikacja odwrotna nie jest prawdziwa.

Uwaga: Pochodną funkcji oznaczamy symbolami:

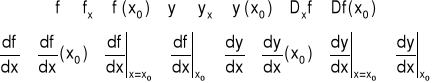
4.2 Pochodna właściwa funkcji funkcji

Obliczanie pochodnej w punkcie wprost z definicji

Przykład 1 Obliczyć z definicji pochodną funkcji f w punkcie x₀

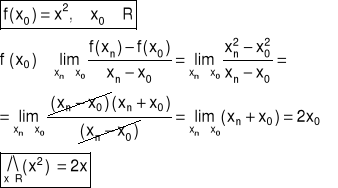
Przykład 2 Obliczyć z definicji pochodną funkcji f w punkcie x₀

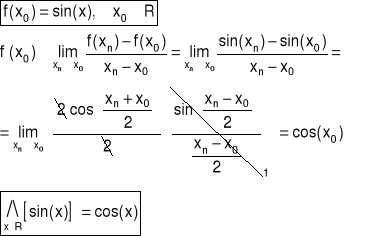
4.2 Pochodna właściwa funkcji funkcji

Obliczanie pochodnej w punkcie wprost z definicji

Przykład 3 Obliczyć z definicji pochodną funkcji f w punkcie x₀

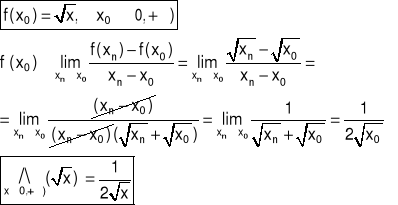
Przykład 4 Obliczyć z definicji pochodną funkcji f w punkcie x₀

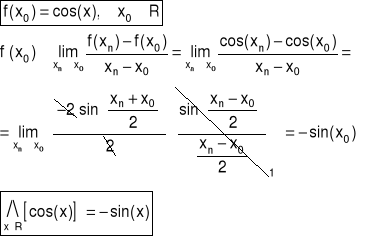
4.2 Pochodna właściwa funkcji funkcji

Obliczanie pochodnej w punkcie wprost z definicji

Przykład 5 Obliczyć z definicji pochodną funkcji f w punkcie x₀

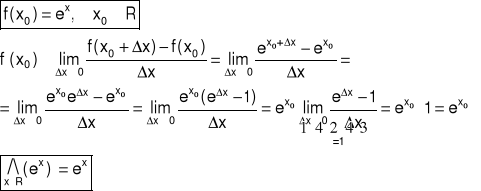
Przykład 6 Obliczyć z definicji pochodną funkcji f w punkcie x₀

4.2 Pochodna właściwa funkcji funkcji

Obliczanie pochodnej w punkcie wprost z definicji

Przykład 7 Obliczyć z definicji pochodną funkcji f w punkcie x₀

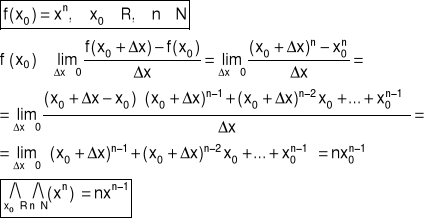
Przykład 8 Obliczyć z definicji pochodną funkcji f w punkcie x₀

4.2 Pochodna właściwa funkcji funkcji

• Interpretacja geometryczna

Niech α oznacza kąt między styczną do wykresu funkcji f w punkcie (x₀, f(x₀)) i dodatnią częścią osi Ox. Wtedy

(4.2.4)

• Interpretacje fizyczne

♦ Niech S(t) oznacza drogę punktu w chwili t. Pochodna

(4.2.5)

oznacza prędkość v poruszającego się punktu w chwili t₀.

Prędkość w ruchu prostoliniowym to pochodna drogi

względem czasu

♦ Niech v(t) oznacza prędkość punktu w chwili t. Pochodna

(4.2.6)

oznacza przyspieszenie a punktu materialnego w chwili t₀.

Przyspieszenie w ruchu prostoliniowym to pochodna

prędkości względem czasu

♦ Niech Q(t) oznacza ilość ładunków elektrycznych, jaka w przedziale czasu Δt przepłynęła przez ustalony przekrój przewodnika. Pochodna

(4.2.7)

oznacza natężenie prądu I w chwili t₀

Natężenie prądu to pochodna ilości ładunków elektrycznych względem czasu

---