Tadeusz Paszkiewicz
Katedra Fizyki
Wydział Matematyki i Fizyki Stosowanej
Politechniki Rzeszowskiej
Układ mechaniczny składający się z punktu
materialnego umieszczonego w jednorodnym
polu grawitacyjnym i poddany takim więzom,
które zezwalają na ruch tego punktu
materialnego wokół pewnego połoŜenia
równowagi.
JeŜeli więzy nałoŜone na ruch wahadła albo
warunki początkowe zostały dobrane tak, aby punkt materialny poruszał się w pewnej
płaszczyźnie pionowej mówimy o wahadle
płaskim.
Realizowane są przez umieszczenie punktu
materialnego na pewnej krzywej albo
powierzchni, zamknięcie w ciasnej rurce,
zawieszenie na nierozciągliwej nici, sztywnym pręcie.
ZałoŜenie
Ruch punktu materialnego odbywa się bez tarcia i w ośrodku nie stawiającym oporu.
Punkt materialny, który znajduje się w polu sił cięŜkości (jednorodnym polu grawitacyjnym) i podczas ruchu musi pozostawać na powierzchni kuli. Ruch zachodzi bez tarcia i oporu powietrza.
Punkt materialny o masie m porusza się po okręgu będącym podstawą stoŜka.
Wahadło cykloidalne
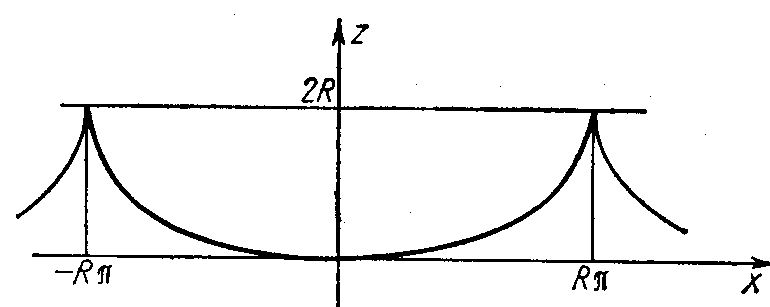
Punkt okręgu o promieniu R toczący się po prostej bez poślizgu zatacza krzywą nazywaną cykloidą.
Równanie cykloidy:
równanie parametryczne : x = R (t − sin t), z = R (t − cos t); równanie ogólne : x = R arccos (R - z) / R − z (2R − z).
Punkt materialny stale porusza się po wybranym łuku cykloidy. Więzy wymuszają ruch po tym łuku.
Dla takiego ruchu: okres T nie zaleŜy od wychylenia: 2π
T =
= 4π R / g .
ω
Własności wahadła cykloidalnego Ruch jest tautochroniczny: jeŜeli prędkość
początkowa punktu materialnego v =0, to czas 0
T potrzebny na przebycie drogi od dowolnego 0
punktu na cykloidzie do jej wierzchołka jest zawsze taki sam:
T = π R / g .
0
Łuk cykloidy jest brachistochroną: czas zsuwania się punktu waŜkiego wzdłuŜ cykloidy od
najwyŜszego do najniŜszego punktu jest
najkrótszy spośród wszystkich krzywych płaskich.
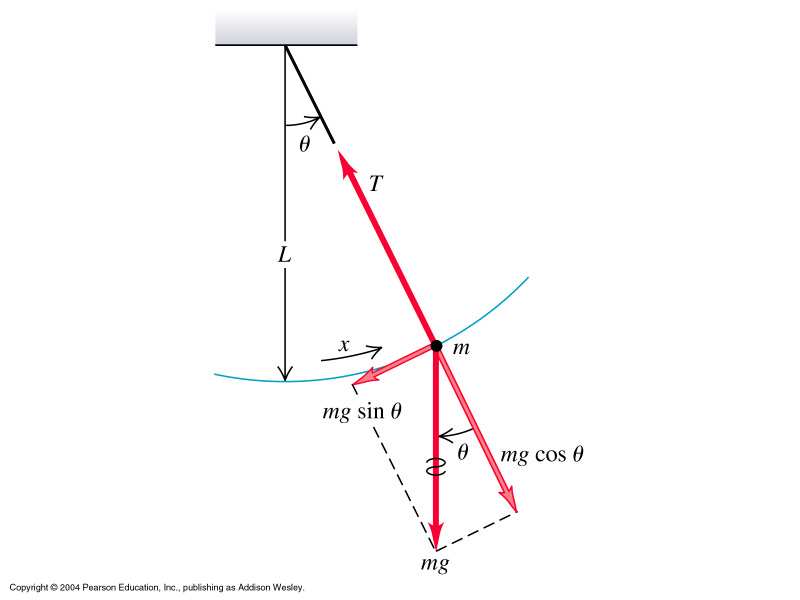
Wahadło koliste (matematyczne) Krzywą więzów jest okrąg
R
φ
m
F = −mgˆz
PołoŜenie równowagi
Początkowe wychylenie z połoŜenia równowagi moŜe być małe, albo duŜe. Rozwiązanie zaleŜy warunków początkowych.
ZaleŜność ruchu wahadła kolistego od warunków początkowych
Warunki początkowe określa początkowy kąt
wychylenia φ i pocz
0
ątkowa prędkość kątowa
φɺ = φɺ t
.
0
( )
Ruch punktu materialnego zaleŜy od
t =0
warunków początkowych.
wahadła kolistego
Wprowadzimy częstość kątową ω:
ω = R / g
1. JeŜeli
k
= ɺ
φ /
2
ω > 1 , to z upływem czasu kąt φ
0
rośnie nieograniczenie – ruch obrotowy po okręgu (przypadek rotacyjny).
2. JeŜeli k=1 i φ =0, to czas potrzebny do osi 0
ągnięcia
górnego punktu okręgu (φ=π) jest nieskończenie długi.
3. JeŜeli k<1, to mamy do czynienia z ruchem oscylacyjnym. Wtedy
φɺ ( t ) cyklicznie zmienia znak.
Wyprowadzenie równania ruchu wahadła kolistego
Przyjmijmy, Ŝe wahadło nie uczestniczy w ruchu postępowym – oś obrotu jest nieruchoma. Punkt materialny pod wpływem momentu siły porusza się po okręgu.
Ruchowi po okręgu towarzyszy nieznikający moment pędu.
Moment siły i moment pędu dla wahadła kolistego
z
Moment siły M :
M = R × F = −mgR × ˆz =
x = −mgR ( ˆx × ˆz sin φ + ˆz × ˆz cos φ) =
φ R
v ⊥ R
st
= −(mgR sin φ) ˆy (za ekran).
m
F
Moment pędu
L :
r
F
st
F
L = R × p = m (R × v) = mR v ˆ
y = (
2
mR )
ωˆy = Iωˆy.
R
ω
I
Równanie ruchu dla wahadła kolistego
dL (t)
dω(t)
= M (t)
I
ˆy = − (mg sin φ) ˆy
dt
dt
2
d φ(t)
I
= −mgsin φ t .
2
( )
dt
2
mR φ
ɺɺ(t) + mgR sin φ(t) = 0.
φɺɺ(t) + (g / R)sin φ(t) = 0.
2
ω
Ostateczna postać równania ruchu wahadła matematycznego
φɺɺ( )
2
t + ω sin φ(t) = 0 .
Dla dowolnego kąta wychylenia rozwiązanie wyraŜa się przez funkcję specjalną – całkę eliptyczną F(k,ψ): ( ψ) ψ
dϕ
F k,
= ∫
.
0
2
2
1− k sin ϕ
Ograniczymy się do małych drgań dookoła połoŜenia równowagi, wtedy
3
sin φ = φ − φ / 6 +… ≈ φ .
małe drgania
φɺɺ( )
2
t + ω φ(t) = 0 .
Częstość ω nie zaleŜy od masy m
ω = g / R .
Okres drgań:
T = 2π R / g .
Rozwiązanie:
φ(t) = φ cos ωt + α .
max
(
)
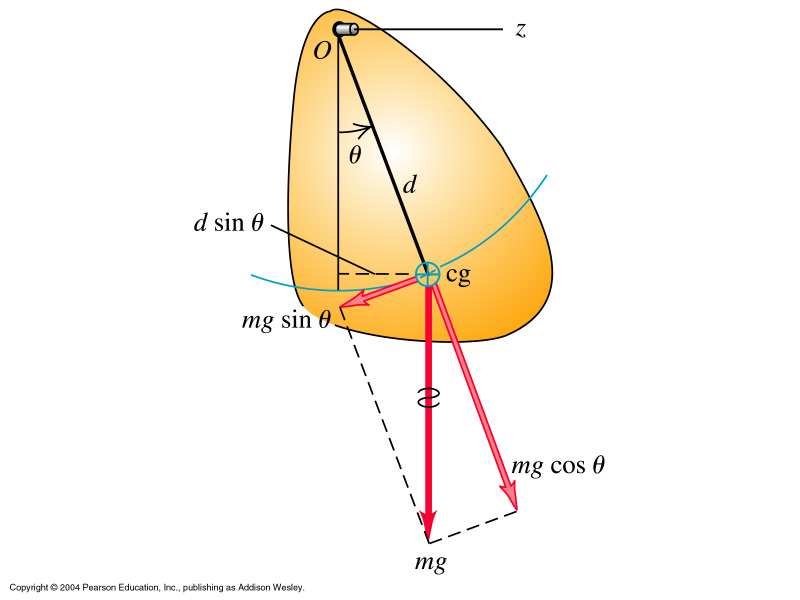
Wahadło fizyczne
d – odległość punktu
zawieszenia od
środka masy c.
Wszystkie siły
działające na
poszczególne
elementy bryły
zastępujemy siłą
wypadkową
F = −mgˆz
zaczepioną w środku
masy bryły.
Moment siły względem osi obrotu:
M = r × (−mgˆz) = −mgd sin θ ˆy .
Moment pędu względem osi obrotu:
L = I
= I dφ / dtˆy = I φɺ
ω
ˆy .
0
0
0
ωˆy
I jest momentem bezwładności bryły
0
względem osi obrotu zamocowanej
w punkcie 0.
wahadła fizycznego
dL
= M ,
dt
2
d θ
I
+ mgdsin θ = 0.
0
2
dt
2
d θ
mgd
+
sin θ = 0.
2
dt
I
0
2
ω
wahadła fizycznego
mgd
ω =
≡ ω .
f
I0
Częstość drgań wahadła fizycznego zaleŜy od masy m, momentu bezwładności, odległości osi od środka masy d i przyśpieszenia swobodnego spadku g.
ω cz
f
ęstość drgań wahadła fizycznego.
wahadła matematycznego i fizycznego
Równania dla wahadła matematycznego i
fizycznego pod względem matematycznym nie
róŜnią się.
Ich rozwiązania teŜ nie róŜnią się
Dla wahadła matematycznego:ω =
g / d.
m
Przyjmijmy d = d = I / md.
0
0
g
g
mgd
ω =
=
=
= ω
m
d
(I / md)
f
I
0
0
0
wahadła fizycznego
Długość d0
d = I / md
0
0
nazywamy długością zredukowaną wahadła
fizycznego. Wahadło fizyczne waha się tak
jak wahadło matematyczne o długości d .
0
Wykorzystanie
twierdzenia Steinera
2
I = md + I
0
c
I – moment bezwładności względem środka masy.
c
d0
d=d0
d
d = I / md =
0 (
) 0
2
md + I
I
c
c
=
= d +
.
md
md
d
dmin
0
dd
x
d
I
I
0 (
)
c
c
=
x +
= 1−
= 0.
2
dx
dx
mx
mx
I
2
c
x =
→ x = I / m .
c
m
d
= I / m .
min
c
odpowiadająca wartości dmin
(min)
I
I
I
m
c
c
c
d
= d +
= d +
= d +
=
0
min
min
min
md
m I / m
m I
min
c
c
= d + I / m = 2d .
min
c
min
dmin
Środek wahań
Na prostej łączącej środek masy C
i oś obrotu z punktu 0 odłoŜymy
odcinek o długości d . Koniec tego
0
θ
d
d odcinka określa punkt 0’, który
0 nazywamy jest ś rodkiem wahań.
d
Twierdzenie:
0 -d
JeŜeli oś obrotu umieścimy
w punkcie 0’, to okres oscylacji
wahadła fizycznego będzie taki
sam jak dla wahadła z osią
obrotu w punkcie 0.
Z twierdzenia Steinera:
2
I = I + md
0
c
d = I / md = d + I / md.
0
0
c
m (d − d = I / d.
0
) c
Długość zredukowana dla osi obrotu przechodzącej przez punkt 0’:
I
I + m d − d
I
/
0'
(
)2
c
0
c
d =
=
=
+ d − d =
0
m (d − d
m d − d
m d − d
0
)
( 0 )
( 0 ) ( 0 )
I / d
c
= d + (d − d = d
0
) 0
Okres drgań bryły zwieszonej w środku wahań T0’
T = 2π d/ / g = 2π d / g = T .□
0'
0
0
0
Dwa równowaŜne
punkty zawieszenia bryły
JeŜeli wahadło zostanie
zawieszone w punkcie 0’, to
θ
d
d0
długość zredukowana, a
więc i okres, są takie same
jak w przypadku zawieszenia
w punkcie 0.
wykorzystywane jest w przypadku
wahadła rewersyjnego