Politechnika Wrocławska^ we Wrocławiu
Paweł Proń	Wydział Elektroniki	kierunek: EIT
data wykonania ćwiczenia: 98-04-07	Grupa: I	rok akademicki: 97/98
Temat ćwiczenia: Statystyczna analiza wyników pomiarów

I. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie ze statystyczną analizą wyników pomiarów, a w szczególności: sposobami znajdowania i eliminacji wyników obarczonych „błędami grubymi”, wyznaczanie i analizy składowej przypadkowej

II. Wyniki pomiarów.

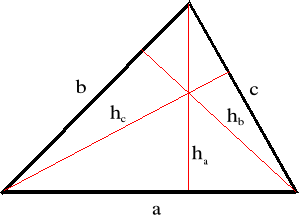
1. Pomiar boków a, b, c i wysokości h_a, h_b, h_c trójkąta przez dwanaście osób.

• rysunek

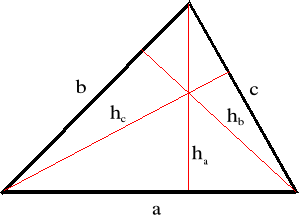
• tabela wyników pomiarów

Lp.	a [mm]	b [mm]	c [mm]	ha [mm]	hb [mm]	hc [mm]	Uwagi
1	95,08	85,33	76,35	65,37	72,67	81,29	błąd graniczny suwmiarki 0,03 [mm]
2	95,08	85,32	76,32	65,17	72,80	81,23
3	95,08	85,33	76,32	65,15	72,68	81,29
4	95,05	85,29	76,28	65,06	72,59	81,28
5	95,05	85,36	76,34	65,63	72,74	81,31
6	95,08	85,32	76,33	65,17	72,62	81,26
7	95,05	85,35	76,33	65,17	72,65	81,23
8	95,66	85,33	76,35	65,19	72,65	81,25
9	95,03	85,34	76,28	65,15	72,62	81,31
10	95,05	85,31	76,35	65,19	72,61	81,28
11	95,07	85,35	76,35	65,20	72,63	81,25
12	94,92	85,22	76,31	65,19	72,64	81,21
m	95,100	85,320	76,325	65,220	72,658	81,265
s	0,1818	0,0370	0,0254	0,1467	0,0592	0,0326

• gdzie: m - wartość średnia

s - odchylenie standardowe średniej

• Uwaga: wartości m i s obliczone przez program extract.exe

1. Po przeanalizowaniu wyników pomiarów nie stwierdziłem występowania błędów grubych.

2. Na podstawie wartości średniej m, odchylenia standardowego średniej s i współczynnika Studenta-Fischera t_N,, określam przedziały ufności wyników.

- dla N = 12,  = 0,95 - t_N, = 1,8

a
< m -
;m +
>

a
< 95,1 -
; 95,1 +
>

a
< 95,1 - 0,4 ; 95,1 + 0,4 >

• pozostałe obliczenia wykonano w ten sam sposób:

b
< 85,32 - 0,07 ; 85,32 + 0,07 >

c
< 76,33 - 0,05 ; 76,33 + 0,05 >

h_a
< 65,22 - 0,27 ; 65,22 + 0,27 >

h_b
< 72,66 - 0,11 ; 72,66 + 0,11 >

h_c
< 81,27 - 0,06 ; 81,27 + 0,06 >

2. Na podstawie wzorów:

P_a =

P_b =

P_c =

P_h =
gdzie: p =

• obliczono pola poszczególnych trójkątów.

• tabela wyników

Lp.	Pa [mm^2]	Pb [mm^2]	Pc [mm^2]	Ph [mm^2]
1	3107,7	3100,5	3103,2	3094,5
2	3098,2	3105,6	3099,7	3093,2
3	3097,2	3100,9	3102,0	3093,5
4	3092,0	3095,6	3100,0	3090,7
5	3119,1	3104,5	3103,6	3094,4
6	3098,2	3098,0	3101,3	3093,5
7	3097,2	3100,3	3100,1	3093,9
8	3118,0	3099,6	3101,7	3103,4
9	3095,6	3098,7	3101,2	3091,7
10	3098,2	3097,2	3102,9	3093,5
11	3099,3	3099,5	3101,7	3094,8
12	3093,9	3095,2	3098,6	3087,8
m	3101,2	3099,6	3101,3	3093,7
s	8,9	3,1	1,5	3,6

• Uwaga: Wszystkie wyniki w tabeli obliczone przez program extract.exe

1. wyznaczam przedziały ufności wyników jak wyżej:

P_a
< 3101,2 - 16,1 ; 3101,2 +16,1 >

P_b
< 3099,6 - 5,6 ; 3099,6 +5,6 >

P_c
< 3101,3 - 2,7 ; 3101,3 +2,7 >

P_h
< 3093,7 - 6,5 ; 3093,7 +6,5 >

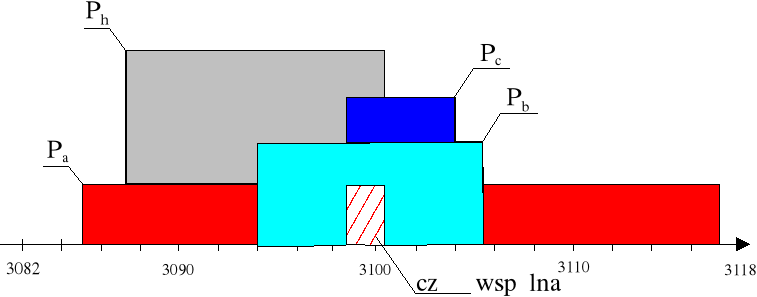
• wykres przedziałów ufności

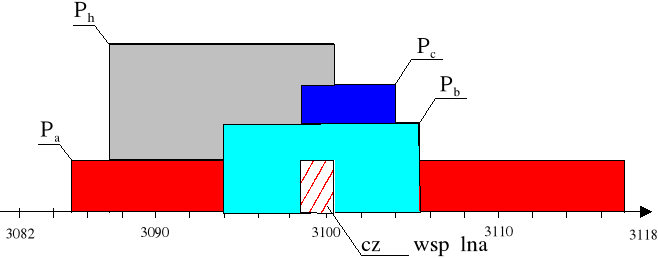
III. Wnioski.

Błędy przypadkowe pomiarów długości boków i wysokości trójkąta wynikają z faktu, że:

• trójkąt mierzyło dwanaście różnych osób z czego wynika, że sposób mierzenia mógł być różny a co za tym idzie - wyniki różne.

Na podstawie wyników pomiarów można wywnioskować, że w trójkącie dokładniej mierzy się długości boków w stosunku do długości wysokości. Wyjątkiem jest bok „a”, którego pomiar jest obarczony większym błędem w stosunku do pozostałych. Może to wynikać z własności geometrycznych tego boku (zaokrąglenia na wierzchołkach - duży promień „r”), należy także zauważyć, że wartość „a” jest największa.

Przy wyznaczaniu pola powierzchni, że duży wpływ na dokładność ma metoda pomiaru tzn. należy dążyć aby obliczenia zawierały jak najmniejszą liczbę pomiarów obarczonych błędem, oraz wybierać te pomiary które są obarczone najmniejszym błędem.

Jeżeli obliczymy pole z długości boku i wysokości i pomiary te są z małym błędem (c, h_c), otrzymane pole jest najdokładniejsze ( P_c ). W przypadku obliczania pola ze wzoru Herona używamy trzech pomiarów obarczonych błędem, które się dodają. Warto też zauważyć, że pole to ma najmniejszą wartość w stosunku do pól liczonych z długości boku i wysokości, gdyż wartości wysokości przy pomiarze są zwykle zawyżone. Z wykresu widać, że pole to odbiega od pozostałych wskutek czego część wspólna jest nieduża. Pozostałe pola pokrywają się w środkach przedziałów ufności.

Politechnika Wrocławska - Instytut Metrologii © 1998

- 4 -

---