nr ćwicz. 101	data 06.04.1994	Sylwia Polińska	Wydział WBL	Semestr IV	grupa O6 nr lab. 5
prowadzący mgr Tomasz Berus					przygotowanie	wykonanie	ocena ostatecz.

TEMAT : WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA REWERSYJNEGO.

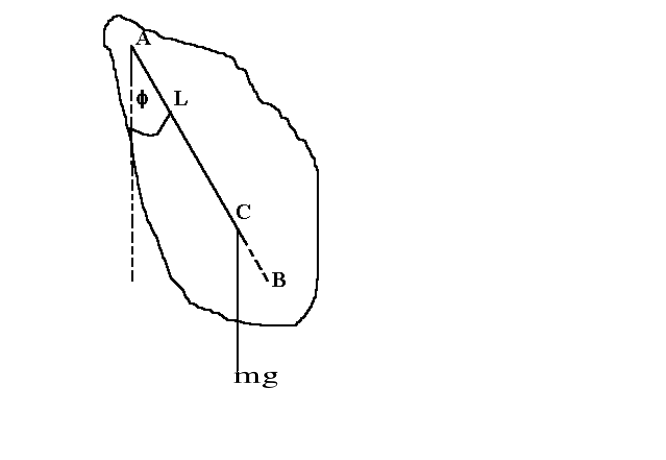
Wahadła fizyczne i matematyczne wykonują ruch drgający pod wpływem działającej siły ciężkości. W zakresie niedużych amplitud ruch ten jest ruchem harmonicznym, jego okres zależy od własności danego wahadła jak również od przyspieszenia ziemskiego.

Wahadłem fizycznym jest każde ciało sztywne mogące się wahać wokół osi poziomej. Po wychyleniu z położenia równowagi na ciało działa moment siły ciężkości :
. Stosując II zasadę dynamiki do tej sytuacji otrzymamy:

, (1)

gdzie: I - moment bezwładności ciała względem punktu zawieszenia A, f - kąt wychylenia od położenia równowagi, L - odległość od punktu zawieszenia A do środka ciężkości C. Znak minus wskazuje, że moment siły zawsze stara się zmniejszyć wychylenie ciała.

Kryterium harmoniczności ruchu będzie spełnione tylko w zakresie małych wychyleń, dla których
. Dla małych wychyleń równanie (1) przyjmie postać:

(2)

Porównując powyższe równanie z ogólnym równaniem ruchu harmonicznego:

, (3)

w którym w oznacza prędkość kątową, uzyskujemy wyrażenie określające okres wahadła fizycznego

, (4)

gdzie D = mgL nazywa się momentem kierującym.

Wahadło matematyczne różni się zasadniczo od wahadła fizycznego rozkładem masy - stanowi je punkt materialny zawieszony na nieważkiej nici. Jeśli długość nici oznaczymy przez l, wówczas okres drgań wahadła matematycznego wyrazi się wzorem

. (5)

Taka długość wahadła matematycznego, dla którego okresy drgań wahadła matematycznego i fizycznego są równe nazywa się długością zredukowaną wahadła fizycznego i wynosi ona:

(6)

Jeżeli znamy długość zredukowaną wahadła fizycznego, wówczas jego okres drgań możemy znaleźć za pomocą równania (5); nie jest do tego konieczna znajomość ani momentu bezwładności, ani momentu kierującego. Do wyznaczenia długości zredukowanej wahadła fizycznego wykorzystujemy tę jego własność, że wahadło zawieszone w punkcie A, a następnie w punkcie B posiada ten sam okres jeżeli odległości pomiędzy punktami zawieszenia jest długością zredukowaną.

Aby wykazać powyższa własność należy znaleźć warunki dla których możliwa jest równość okresów.

, (7) gdzie AB = l

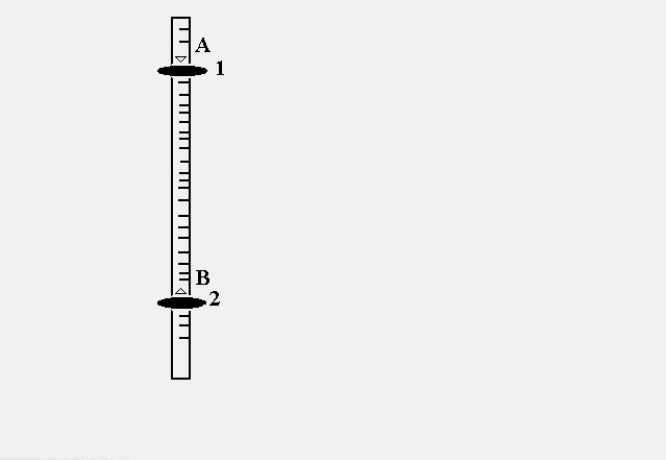
Momenty bezwładności względem osi przechodzących przez punkty A i B można wyrazić przez moment
względem osi równoległej przechodzącej przez środek ciężkości:

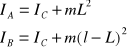
Wówczas

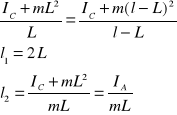
Wartość
odpowiada przypadkowi, gdy oba punkty zawieszone są symetrycznie względem środka ciężkości, natomiast
jest właśnie długością zredukowaną.

Specjalną postacią wahadła fizycznego jest wahadło rewersyjne lub odwracalne ( rysunek obok). Na długim pręcie znajdują się dwa ciężarki w kształcie soczewek, które mogą być przesuwane wzdłuż pręta. Osie obrotu A i B mają postać pryzmatów metalowych i mogą być przesuwane wzdłuż pręta.

PRZEBIEG ĆWICZENIA

1. Umocować ostrza A i B w odległości wzajemnej
= 0.8 - 1.1 m. Soczewkę 2 umocować w pobliżu końca wahadła.

2. Umocować soczewkę 1 w pobliżu ostrza B.

3. Zmierzyć czas 10 wahnięć wahadła zawieszonego wpierw na ostrzu A a następnie na ostrzu B. Obliczyć odpowiednie okresy
.

4. Zmieniając położenie soczewki 1 co 5 - 10 cm w całym zakresie między ostrzami 1 i 2 powtarzać pomiar okresów
.

5. Wykonać wykresy okresów
w funkcji położenia soczewki 1. Punkt przecięcia się krzywych
wyznacza okres T jednakowy dla obu zawieszeń.

6. Ustawić ponownie soczewkę 1 w położeniu odpowiadającym punktowi przecięcia się krzywych i jak najdokładniej sprawdzić, czy
. W razie niegodności okresów dokonać małych przesunięć soczewki, aż do zupełnego zrównania się okresów.

7. Obliczyć przyspieszenie ziemskie ze wzoru

.

8. Zmienić odległość miedzy ostrzami i powtórzyć punkty 2 - 7.

---