Nr ćwicz. 101	Data: 99.10.21	Paweł Szwec	Wydział Elektryczny	Semestr III	Grupa A - 2
Prowadzący: dr A. Skibiński					Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat : Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego .

Wahadła fizyczne i matematyczne wykonują ruch drgający pod wpływem siły ciężkości . Jeżeli amplituda jest stosunkowo niewielka to ruch jest harmoniczny .Wahadłem fizycznym nazywamy ciało sztywne mogące wahać się wokół własnej osi.

Z drugiej zasady dynamiki dla powyższego rysunku otrzymujemy :

(*) ,

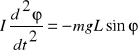
gdzie I - moment bezwładności ciała ,

 - kąt wychylenia od położenia równowagi ,

L - odległość od punktu zawieszenia A do środka ciężkości C .

W ruch harmonicznym przyspieszenie jest wprost proporcjonalne do wychylenia . Porównując to stwierdzenie ze wzorem (*) można zauważyć , że ruch wahadła fizycznego jest harmoniczny jedynie dla małych wychyleń (wtedy bowiem sin 

Przy założeniu małych wychyleń można zapisać :

.

Z porównania powyższego równania z ogólnym równaniem ruchu harmonicznego :

,

(  jest prędkością kątową ) ,

otrzymujemy :

, D - moment kierujący ( D=mgL ) .

Wahadło matematyczne różni się tym od fizycznego , że cała masa układu jest skupiona w jednym punkcie ( który jest oczywiście środkiem ciężkości ). Połączenie pomiędzy środkiem ciężkości a punktem zawieszenia interpretuje się jako nieważką nić o długości l. Okres drgań takiego wahadła wyraża się wzorem :

(**).

Mając dane dwa wahadła fizyczne i matematyczne można dobrać tak długość wahadła matematycznego by miało ono okres równy wahadłu fizycznemu . Tę długość nazywamy długością zredukowaną wahadła

fizycznego . Wyraża się ona wzorem :

`
.

Teraz można wyznaczyć okres wahadła fizycznego ze wzoru (**) .

By wyznaczyć długość zredukowaną korzysta się z następującej własności : wahadło zawieszone w punkcie A , a następnie w B ( patrz rysunek powyżej ) posiada taki sam okres , jeżeli odległość pomiędzy tymi punktami jest długością zredukowaną .W ćwiczeniu do określenia tego okresu stosuje się wahadło rewersyjne.

Przebieg ćwiczenia .

1. Wprowadzić w szczelinę czujnika fotoelektrycznego kulkę wahadła matematycznego . Uregulować jego długość tak , aby kreska na kulce była na jednym poziomie z kreską zaznaczoną na czujniku . Odczytać długość wahadła .

2. Wychylając wahadło o niewielki kąt zmierzyć czas 10 wahnięć .Obliczyć okres T wahadła matematycznego .

3. Pomiary powtórzyć co najmniej dla trzech różnych długości wahadła .

4. Znając okres T i długość wahadła matematycznego obliczyć przyspieszenie ziemskie .

5. Umocować ostrza A i B w odległości wzajemnej lr=0.8-1.1 m .Soczewkę 2 umocować w pobliżu końca wahadła .

6. Umocować soczewkę 1 w pobliżu ostrza B .

7. Zmierzyć czas około 10 wahnięć wahadła zawieszonego najpierw na ostrzu A , a następnie na ostrzu B. Obliczyć odpowiednie okresy TA i TB .

8. Zmieniając położenie soczewki 1 co 5 - 10 cm w całym zakresie między ostrzami 1 i 2 powtarzać pomiar okresów TA i TB .

9. Wykonać wykresy okresów TA i TB w funkcji położenia soczewki 1 . Punkt przecięcia się krzywych TA i TB wyznacza okres T .

Wahadło matematyczne .

Z równania (**) otrzymujemy wzór na przyspieszenie ziemskie :

Błąd :

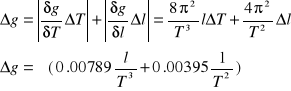
Dla poszczególnych danych z tabeli 1 ( po uśrednieniu okresu ) przyspieszenia i ich błędy :

g1 = 9.814628 ms-2 , g1=0.003031 ms-2 ,

g2 = 9.784444 ms-2 , g2=0.003044 ms-2 ,

g3 = 9.835221 ms-2 , g3=0.002246 ms-2 .

Średnia pomiaru :

Odchylenie standardowe średniej :

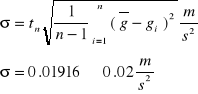
Przyspieszenie wynosi :

g = 9.81 0.02 ms-2 .

Wahadło rewersyjne .

Ponieważ wykresy dla obu zawieszeń nie przecięły się konieczne jest zastosowanie ekstrapolacji . Na wykresie 1 przedstawione są wyniki pomiarów dla obu zawieszeń ( bez uwzględnienia błędów ) , po odrzuceniu pomiaru w odległości 0.075 m , który wyraźnie odbiega

od reszty ( dla okresu TA) ze względu na kształt wykresu , prowadzimy prostą przechodzącą przez dwa ostatnie punkty pomiarowe ( odległości 0.08 m i 0.11 m ) . Obie proste przetną się

w punkcie odpowiadającym odległości ok. l=0.018 m i okresowi T=2.0437 s . Sytuację taką przedstawia wykres 2 .

Przyjmujemy :

T = 2.044 s

l = 0.02 m ( z uwagi na dokładność przyrządów ) .

Przyspieszenie będzie równe :

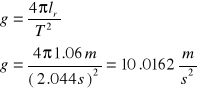
Błąd pomiaru przyspieszenia wyraża się analogicznym wzorem jak dla wahadła matematycznego i wynosi :

g=0.0946 ms-2 .

Wynik pomiaru :

g = 101 ms-2 .

Wnioski .

Przeprowadzone doświadczenie udowodniło , że dokładniejszego pomiaru przyspieszenia można dokonać wahadłem matematycznym ( ściślej zbliżonym do matematycznego ) niż wahadłem rewersyjnym . Przyspieszenie ziemskie wynosi :

g = 9.80665 ms-2 .

Zatem wyniki obu pomiarów są poprawne . Jednak w przypadku wahadła rewersyjnego jest stosunkowo duża różnica . Może być to wynikiem zastosowania ekstrapolacji ze względu na to , że bezpośredni pomiar okresu stał się w praktyce niemożliwy . Wpływ na dokładność pomiaru przyspieszenia wahadłem rewersyjnym ma również ma duża niedokładność miary wyskalowanej na pręcie . Wyniki pomiaru znacznie polepsza dokładne urządzenie mierzące okres .

---