Numer ćwiczenia

Data:

Marcin Skrzypczak

FIZYKA

Semestr III Grupa B

Ocena:

Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego .

Wahadła fizyczne i matematyczne wykonują ruch drgający pod wpływem siły ciężkości . Jeżeli amplituda jest stosunkowo niewielka to ruch jest harmoniczny .Wahadłem fizycznym nazywamy ciało sztywne mogące wahać się wokół własnej osi.

Z drugiej zasady dynamiki dla powyższego rysunku otrzymujemy :

(*) ,

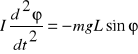
gdzie I - moment bezwładności ciała ,

 - kąt wychylenia od położenia równowagi ,

L - odległość od punktu zawieszenia A do środka ciężkości C .

W ruch harmonicznym przyspieszenie jest wprost proporcjonalne do wychylenia . Porównując to stwierdzenie ze wzorem (*) można zauważyć , że ruch wahadła fizycznego jest harmoniczny jedynie dla małych wychyleń (wtedy bowiem sin 

Przy założeniu małych wychyleń można zapisać :

.

Z porównania powyższego równania z ogólnym równaniem ruchu harmonicznego :

,

(  jest prędkością kątową ) ,

otrzymujemy :

, D - moment kierujący ( D=mgL ) .

Wahadło matematyczne różni się tym od fizycznego , że cała masa układu jest skupiona w jednym punkcie ( który jest oczywiście środkiem ciężkości ). Połączenie pomiędzy środkiem ciężkości a punktem zawieszenia interpretuje się jako nieważką nić o długości l. Okres drgań takiego wahadła wyraża się wzorem :

(**).

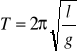
Mając dane dwa wahadła fizyczne i matematyczne można dobrać tak długość wahadła matematycznego by miało ono okres równy wahadłu fizycznemu . Tę długość nazywamy długością zredukowaną wahadła

fizycznego . Wyraża się ona wzorem :

`
.

Teraz można wyznaczyć okres wahadła fizycznego ze wzoru (**) .

By wyznaczyć długość zredukowaną korzysta się z następującej własności : wahadło zawieszone w punkcie A , a następnie w B ( patrz rysunek powyżej ) posiada taki sam okres, jeżeli odległość pomiędzy tymi punktami jest długością zredukowaną .W ćwiczeniu do określenia tego okresu stosuje się wahadło rewersyjne.

Wahadło rewersyjne .

L.p.	dla 52 cm	dla 40 cm	dla 25 cm
1.	14,463	12,658	9,995
2.	14,466	12,660	9,990
3.	14,473	12,664	9,999

t=0,001 [s]

Uśredniając wartości w kolumnach otrzymujemy średni czas 1 wachnięcia (błąd to 1,33odch. st.):

	dla 52 cm	dla 40 cm	dla 25 cm
	1,4467	1,2661	0,9995
	0,002001	0,001191	0,001759

Z równania otrzymujemy wzór na przyspiesznie ziemskie:

Otrzymujemy zatem odpowienio:

	dla 52 cm	dla 40 cm	dla 25 cm
g	9,98812	9,97159	9,89014
g	0,045998	0,043171	0,07429

w końcu uśredniając powyższe pomiary otrzymujemy:

g=9,9500,055 [m/s2]

Pomiary dla 10 wachnięć wahadła rewersyjnego w różnych położeniach soczewki nr 1; ostrze A znajduje się na 16 cm, B--na 127 cm, a soczewka nr 2 na 131,5 cm

wisząc na:	115 cm	110 cm	100 cm	90 cm	80 cm	60 cm
A	20,473	20,304	19,971	19,725	19,523	19,399
B	17,781	17,215	16,675	16,601	16,834	17,817

Otrzymujemy wykres:

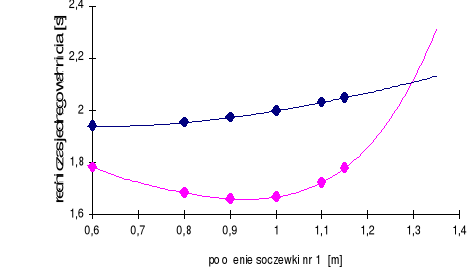
ponieważ krzywe nie przecinają się, przeprowadzono ekstrapolowanie o kilka punktów w przód krzywą stopnia czwartego, co pozwolilo osiągnąć przecięcie w punkcie o współrzędnych: (1,31 [m], 2,2 [s] )
Daje to zgodnie ze wzorem analogicznym jak w poprzednim punkcie otrzymujemy:

g=10,6 [m/s2]

Błąd g jest w tym przypadku trudny do oszacowania (nie wiadomo jak bardzo powiększa go ekstrapolowanie). Jednakże przy założeniu, że l=0,02 [m], a t=0,05 [s], to korzystając z przytoczonego wcześniej wzoru wykorzystującego rózniczkę zupełną otrzymujemy g=0,6 [m/s2]

Wnioski .

W wyniku moich pomiarów za pomocą wahadła rewersyjnego - przyspieszenie ziemskie wynosi :

g=9,9500,055 [m/s2]

Wpływ na dokładność pomiaru przyspieszenia wahadłem rewersyjnym ma duża niedokładność miary wyskalowanej na pręcie .

Przyrządy, którymi posługiwałem się podczas pomiarów były niedokładne.

Na wynik wpłynęły też błędy wynikające z mierzenia czasu stoperem i „ludzką ręką”.

---