STATYSTYKA	www.pure6.neostrada.pl
Wykład - 18.03.2004.	By GLad|

Parametry rozkładu zmiennej losowej dwuwymiarowej

E(x), E(y) - wartość oczekiwana (przeciętna)

D²(x), D²(y) - wariancja

D(x), D(y) - odchylenie standardowe

C(x, y) - kowariancja

C(x, y) = E{[x - E(x)] * [y - E(y)]}

Jeśli składowe x, y są niezależne to C(x, y) = 0

Współczynnik korelacji:

Ρ (ro) =

-1 ≤ Ρ ≤ 1

Parametry rozkładu dwuwymiarowej zmiennej losowej skokowej

E(x) =

E(y) =

D²(x) =

D(y) =

Ρ(x, y) =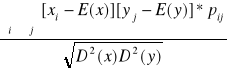

Parametrami zmiennej dwuwymiarowej jest:

- wartości zmiennej

- wariancja

- kowariancja

- odchylenie

Warunkowa wartość przeciętna (ma postać funkcji)

E(Y/X = x) = g₁(x)

Jeśli E(Y/X = x) = y to y = g₁(x)

Jeśli E(X/Y = y) = x to x = g₂(y)

Funkcje regresji pierwszego rodzaju:

y = g₁(x)

x = g₂(y)

Jeśli postać analityczna funkcji g nie jest znana to poszukujemy takiej postaci funkcji g aby:

E[Y - g₁(x)]² = min (kryterium najmniejszych kwadratów),

wtedy funkcja g jest funkcją regresji drugiego rodzaju.

Można graficznie przedstawić wykres zmiennej losowej dwuwymiarowej w postaci np. histogramu.

Zmienna losowa wielowymiarowa

X = [X₁, X₂, …, X_k]

X =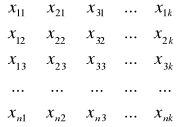

Parametry rozkładu zmiennej losowej wielowymiarowej

E = [E(X₁), E(X₂), …, E(X_k)]

D =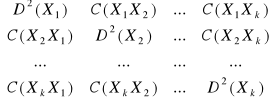

R =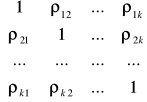

współczynnik korelacji cząstkowej

współczynnik korelacji wielorakiej

---