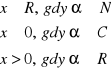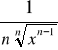Pochodna funkcji

Zakładamy, że funkcja f jest określona w pewnym otoczeniu U punktu x₀. Niech
oznacza różny od zera przyrost zmiennej x taki, że punkt
.

Wyrażenie

nazywamy ilorazem różnicowym funkcji f w punkcie x₀ dla przyrostu
zmiennej x.

Def. Jeżeli istnieje skończona granica

to nazywamy ją pochodną funkcji f w punkcie x₀.

Pochodną funkcji f w punkcie x₀ oznaczamy symbolem
lub
.

Definicję tę można zapisać równoważnie

Uwagi:

1. O funkcji f mającej pochodną w punkcie x₀ mówimy, że jest różniczkowalna w punkcie x₀.

2. Obliczanie pochodnych nazywamy różniczkowaniem.

Pochodne nieskończone

3. Jeżeli granica ilorazu różnicowego jest równa +∞ lub -∞,to mówimy, że funkcja ma w danym punkcie pochodną nieskończoną równą +∞ lub -∞..

Geometryczny sens pochodnej

Pochodna
jest równa tangensowi kąta, jaki tworzy z osią Ox styczna poprowadzona do wykresu funkcji f w punkcie

Styczna ta ma równanie

Jeżeli funkcja f ma pochodną w każdym punkcie zbioru X, to na zbiorze X określona jest funkcja, którą nazywamy funkcją pochodną funkcji f , krótko pochodną funkcji f i oznaczamy
.

Pochodne Jednostronne

Granice jednostronne ilorazu różnicowego (o ile istnieją)

nazywamy odpowiednio lewostronną i prawostronną pochodną funkcji f w punkcie x₀.

Używamy także oznaczeń
,

Wniosek

Pochodna
istnieje wtedy i tylko wtedy, gdy obie pochodne jednostronne istnieją i są sobie równe.

Pochodna w przedziale

Jeśli funkcja f ma pochodną w przedziale (a, b) oraz istnieją
,
to mówimy, że istnieje pochodna funkcji f na przedziale domkniętym
.

TW: (istnienie pochodnej a ciągłość; warunek konieczny istnienia pochodnej) dowód

Jeżeli funkcja f ma pochodną w punkcie x₀, to jest w tym punkcie ciągła.

Tw. odwrotne nie zachodzi.

Funkcja ciągła w pewnym punkcie może nie mieć w tym punkcie pochodnej np.
jest ciągła w punkcie x₀=0, ale nie ma w tym punkcie pochodnej.

Obliczanie pochodnych

Tw:

Jeżeli funkcje f , g są różniczkowalne w punkcie x, to ich suma, różnica, iloczyn są różniczkowalne w punkcie x i zachodzą równości

(dowód)

ponadto

gdzie c oznacza stałą.

Jeżeli założymy, że
, to iloraz
jest różniczkowalny w punkcie x i zachodzi równość

Tw. ( o pochodnej funkcji odwrotnej)

Jeżeli funkcja
jest ściśle monotoniczna i ma pochodną
na przedziale Y, to funkcja odwrotna
ma na przedziale f(Y) pochodną daną wzorem

Tw. (o pochodnej funkcji złożonej)

Jeżeli funkcja h ma pochodną w punkcie x oraz funkcja g ma pochodną w punkcie u gdzie
, to funkcja złożona
ma pochodną w punkcie x daną wzorem

.

Równość tę wygodnie zapisać

Pochodna logarytmiczna

Pochodną logarytmiczną funkcji f nazywamy pochodną jej logarytmu naturalnego

Pochodne wyższych rzędów

Jeżeli funkcja
ma pochodną
w zbiorze X, to tę pochodną nazywamy pochodną rzędu drugiego funkcji f w zbiorze X i oznaczamy
.

Analogicznie określamy pochodne wyższych rzędów.

Pochodna rzędu n funkcji f jest to pochodna pochodnej rzędu n-1

.

Pochodną rzędu n zapisujemy również

Zadanie

Wyznaczyć pochodną n-tego rzędu funkcji
.

		uwagi
	0	funkcja stała

19