Laboratorium Fizyki	Numer ćw M 12	Data ćw: 9-III-98		Grupa: 11M	Politechnika Świętokrzyska w Kielcach
Temat ćwiczenia: LICZNIK GEIGERA-MULLERA
Wykonał: Kiniorski Rafał			Ocena:			Data:	Podpis:

1. Wiadomości wstępne.

Licznik Geigera-Mullera jest obecnie najczęściej stosowanym przyrządem do rejestracji promieniowania jądrowego. Składa się on z metalowego cylindra o średnicy kilku cm, wypełnionego gazem szlachetnym z niewielkim dodatkiem par alkoholu. W środku cylindra biegnie cienki , odizolowany drut, stanowiący anodę, którego potencjał musi być dodatni.

Pomiędzy uziemionym cylindrem a drutem tworzy się silne pole elektryczne. Cząstka przechodząca przez objętość czynną licznika powoduje powstawanie wewnątrz licznika jonów, które przyspieszone silnym polem elektrycznym tworzą lawinę jonów dodatnich i elektronów. Te ostatnie ze względu na małą masę bardzo szybko osiągają anodę, powodując przepały prądu przez opór R i tak duży spadek napięcia U na anodzie, że przerywa on dalszy rozwój lawiny. Ten krótkotrwały spadek napięcia nosi nazwę impulsu.

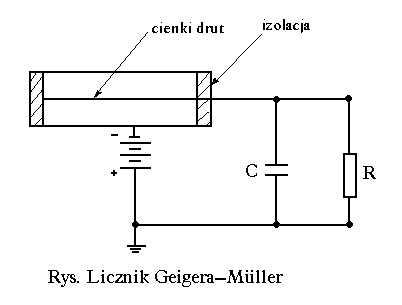
Rejestrując poszczególne impulsy, z których każdy odpowiada przejściu przez licznik pojedynczej cząstki, możemy ustalić liczbę cząstek przechodzących przez licznik. Kiedy napięcie pomiędzy anodą (drutem) i katodą (cylindrem) ma zbyt ma-łe wartości licznik rejestruje tylko część liczby cząstek, jakie przechodzą przez jego objętość czynną. Dopiero kiedy napięcie osiągnie tzw. wartość progową na-stępuje rejestracja wszystkich cząstek. Zależność liczby rejestrowanych cząstek od przyłożonego napięcia nosi nazwę charakterystyki licznika Gaigera-Mullera.

Cześć krzywej równoległa do osi napięcia nosi nazwę plateau. W trakcie wykonywania pomiarów należy tak dobrać napięcie , aby przypadło ono w środku plateau. Nosi ono nazwę napięcia pracy. Przekroczenie napięcia krytycznego grozi zniszczeniem licznika.

Obok wielu zalet, do których należy duże napięcie impulsów pozwalające pracować bez wzmacniaczy, licznik ten ma istotną wadę polegającą na tym, że nie można określić energii rejestrowanej cząstki. Licznik G-M rejestruje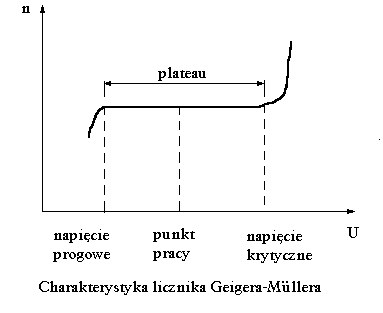
jedynie fakt przejścia cząstki, a to do wielu pomiarów absolutna wystarcza. Ze względu na prostotę działania licznik ten znalazł szerokie zastosowanie zarówno w nauce jak i w technice.

2. przebieg ćwiczenia.

• Wyznaczanie plateau:

W celu wyznaczenia obszaru plateau należy nastawić czas zliczania licznika Geigera-Mullera na 10 min, następnie uruchomić zliczanie i potencjometrem płynnej regulacji stopniowo podnosić napięcie na zasilaczu do momentu kiedy przelicznik zacznie zliczać impulsy. W przypadku mojego doświadczenia licznik zaczął zliczać impulsy przy napięciu 430V .

Kolejnym etapem jest zresetowanie wartości impulsów na przeliczniku i ponowne ustawienie czasu zliczania , tym razem na 1 min. Zmieniając napięcie co 10V , poczynając od napięcia 430V ( wyznaczonego wcześniej), za każdym razem odczytuję liczbę impulsów , aż do chwili kiedy nastąpi ich gwałtowny skok. Zależność liczby impulsów od napięcia zapisuje w tabeli, a według niej sporządzam wykres :

V	R
430	3
440	83
450	156
460	313
470	414
480	413
490	387
500	400
510	388
520	391
530	434
540	399
550	444
560	476
570	487
580	616
590	985

• Na podstawie wykresu wyznaczam liczbę zliczeń na początku plateau (R₁) i na końcu plateau (R₂) : R₁ = 414, R₂ = 444

• Wyznaczam wartość średnią R_śr pomiarów:

• Obliczam odchylenie standardowe:

• Wyznaczam nachylenie plateau ze wzoru:

% =1,86 %

• Ustawiam napięcie na liczniku w obrębie plateau (napięcie pracy = 510V

i notuję liczbę impulsów w 50-ciu kolejnych, niezależnych pomiarach. Czas

zliczania ustawiam na 1min. Wyniki umieszczam w tabeli:

N	Ri				N	Ri
1	388	- 0,98	-1		26	386	- 1,08	-1
2	388	- 0,98	-1		27	421	0,65	0,5
3	413	0,26	0,5		28	413	0,26	0,5
4	362	- 2,27	-2,5		29	410	0,11	0
5	378	- 1,48	-1,5		30	389	- 0,93	-1
6	361	- 2,32	-2,5		31	428	1,00	1
7	407	- 0,04	0		32	408	0,01	0
8	441	1,64	1,5		33	396	- 0,58	-0,5
9	446	1,89	2		34	364	- 2,17	-2
10	394	- 0,68	- 0,5		35	399	- 0,44	-0,5
11	402	- 0,29	- 0,5		36	432	1,20	1
12	421	0,65	0,5		37	418	0,50	0,5
13	392	- 0,78	-1		38	380	- 1,38	-1,5
14	387	- 1,03	-1		39	409	0,06	0
15	391	- 0,83	-1		40	394	- 0,68	-0,5
16	385	- 1,13	-1		41	370	- 1,87	-2
17	412	0,21	0		42	374	- 1,67	-1,5
18	406	- 0,09	0		43	393	- 0,73	-0,5
19	375	- 1,62	-1,5		44	415	0,36	0,5
20	376	- 1,57	-1,5		45	373	- 1,72	-1,5
21	400	- 0,39	-0,5		46	369	- 1,92	-2
22	375	- 1,62	-1,5		47	395	- 0,63	-0,5
23	387	- 1,03	-1		48	410	0,11	0
24	397	- 0,53	-0,5		49	406	- 0,09	0
25	444	1,79	2		50	417	0,46	0,5

• Na podstawie danych tablicowych obliczam krzywą Gaussa:

Odstępstwo od odchylenia względnego	Ilość powtórzeń	f(ui) (krzywa Gaussa)
-2,5	2	0,43825
-2	3	1,3482
-1,5	7	3,2375
-1	9	6,05
-0,5	9	8,8025
0	8	9,9725
0,5	6	8,8025
1	2	6,05
1,5	1	3,2375
2	1	1,3482
2,5	0	0,43825

• Na podstawie pomiarów sporządzam histogram i porównuję go z krzywą normalnego rozkładu błędów statystycznych Gaussa :

2. Wnioski:

Wykres zamieszczony powyżej ma zbliżony kształt do krzywej normalnego rozkładu błędów Gaussa . Najwięcej razy powtórzyły się najmniejsze odstępstwa od odchylenia względnego, a bardzo mało było wyników znacznie różniących się od tego odchylenia. Można się domyślić ,

że przy większej ilości pomiarów różnica ta byłaby jeszcze bardziej widoczna.

IV

Ilość powtórzeń

Rys. Licznik Geigera-Mullera.

Odstępstwo od odchylenia względnego

---