MECHANIKA (wykłady)

Problem I: Czy punkt przyłożenia siły działającej na ciało sztywne jest istotny?

Do jednoznacznego określenia siły potrzebne są:

• kierunek (prosta k) działania

• zwrot

• wartość (długość wektora)

• punkt przyłożenia (zaczepienia)

Punkt przyłożenia siły może być przemieszczany wzdłuż linii działania tej siły. Siłę można przesuwać wzdłuż linii jej działania do dowolnego punktu (wektor ślizgający się).

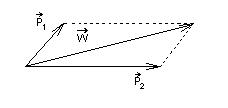
Problem II: Czy dwie nierównoległe siły działające na ciało w jednej płaszczyźnie można zastąpić wypadkową?

W - siła wypadkowa

Można zastąpić dwie siły działające na ciało siłą wypadkową, przesuwając wzdłuż prostej działania (linii) siły do punktu przecięcia (zbieżności)

Problem III: Czy zawsze dwie nierównoległe siły przyłożone do ciała można zastąpić wypadkową?

Nie zawsze lecz tylko wtedy gdy linie działania sił leżą w jednej płaszczyźnie. Jeśli linie działania sił są ukośne do siebie czyli nie przecinają się to dwóch sił nie można zastąpić wypadkową.

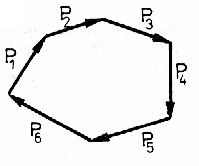
RÓWNAWAGA PŁASKIEGO UKŁADU SIŁ ZBIEŻNYCH

Równowaga układu sił - wzajemnie równoważącej się wypadkowej nie ma (jest równa zero)

Wielobok sił jest zamknięty, jest to warunek wykreślny równowagi Płaskiego Układu Sił Zbieżnych

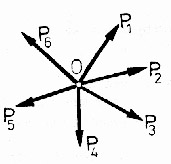
W_x=0 warunki analityczne

W_y=0 równowagi PUSZ

Problem IV: Na ciało działają trzy równoległe siły, które się wzajemnie równoważą. Co można powiedzieć o tych siłach?

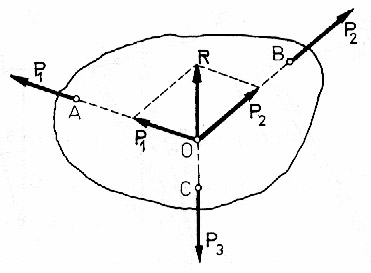
- jedna z tych sił np. P₃ powinna zrównoważyć dwie pozostałe P₁ i P₂

- te dwie pozostałe siły powinny mieć wypadkową

- wypadkowa ta musi równoważyć się z wypadkową P₃

- wszystkie trzy siły muszą leżeć w jednej płaszczyźnie

- linie działania tych sił muszą przecinać się w jednym punkcie (twierdzenie o trzech siłach)

MOMENT SIŁY WZGLĘDEM PUNKTU. PARA SIŁ.

O - biegun momentu

r - promień wodzący

M_O - moment siły

M_O(P) - iloczyn wektorowy promienia wodzącego r i siły P

Wartość momentu:

siła x ramię działanie siły

Moment siły: 1N∙1m=1Nm (niutonometr)

Zasada przypisywania znaków:

Tw. VARIGNONA: Moment wypadkowej 2 sił względem dowolnego punktu równy jest sumie momentów tych sił względem tego punktu.

Problem V: Czy dwie siły równoległe o jednakowych zwrotach można zastąpić wypadkową?

1. jest równoległa do tych sił

2. 
   ma ten sam zwrot

3. jej wartość jest równa sumie wartości tych sił

4. jej linia działania dzieli odcinek AB łączący punkty przyłożenia tych sił w stosunku odwrotnie proporcjonalnym do wartości tych sił

0

Odp. Można zastąpić siłą wypadkową

Problem VI: Czy 2 siły równoległe o jednakowych wartościach i przeciwnych zwrotach wywierają skutek na ciało?

Tak , wywierają skutek. 2 siły równoległe o jednakowych wartościach i przeciwnych zwrotach tworzą parę sił.

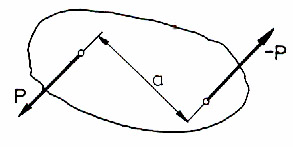
Para sił należy do podstawowych wielkości mechanicznych obok siły i momentu siły.

Teoria pary sił

Można wyznaczyć moment pary sił M=P∙a

P - siła

a - odległość a między liniami sił

Równoległe przesunięcie siły

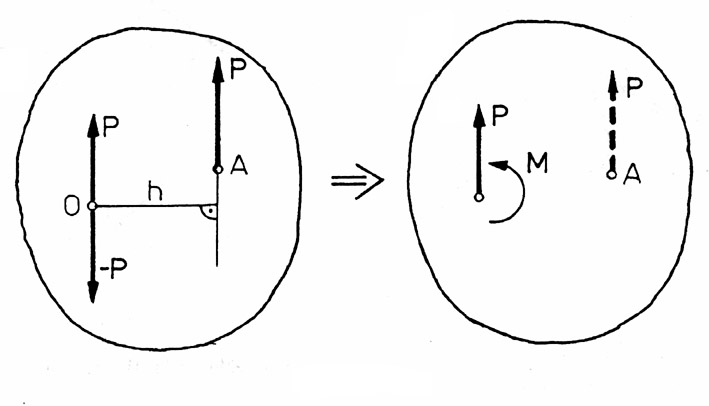
Siłę można przesunąć równolegle do jej początkowego położenia i zaczepić ją w innym punkcie dodając odpowiedni moment M.

Redukcja DPUS (dowolnego płaskiego układu sił)

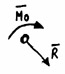
Dowolny układ sił działający na ciało sztywne możemy zastąpić wektorem głównym
przyłożonym w dowolnym biegunie O oraz momentem głównym
względem tego bieguna

WEKTOR GŁÓWNY

MOMENT GŁÓWNY

Dowolny płaski układ sił jest w równowadze gdy suma geometryczna tych sił oraz suma algebraiczna ich momentów względem dowolnego punktu płaszczyzny sił są równe zeru.

2 postać równań równowagi dowolnego płaskiego układu sił

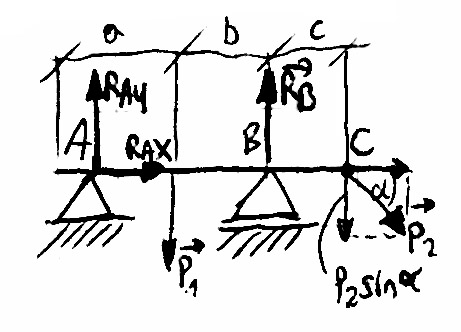
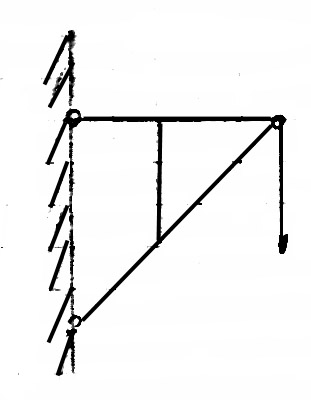
ZAD. Układ mechaniczny składa się z poziomego nieważkiego pręta podpartego na podporze stałej A i podporze przesuwnej B. Pręt obciążony jest dwoma siłami czynnymi
i
. Ułożyć równania równowagi jeżeli dane są P₁, P₂, α, a, b, c

Rozwiązanie: 1) Wyodrębnić układ mechaniczny pręta AC

2) Siły czynne
i
są

3) siły reakcji
i

- znany kierunek - pionowy

- nieznany kierunek (składowe
i
)

4) Wyprowadzamy układ osi x,y

5) Układ równań równowagi sił wyznaczamy wykorzystując I postać układu równań równowagi

W celu sprawdzenia poprawności wyników można ułożyć dodatkowe równanie równowagi i sprawdzić czy jest ono spełnione dla obliczonych wartości reakcji.

TARCIE

CHARAKTERYSTYKI GEOMETRYCZNE FIGUR PŁASKICH

Elementy konstrukcyjne, które poddawane są obliczeniom wytrzymałościowym mają zwykle postać prętów, w których jeden wymiar jest znacznie większy od dwóch pozostałych. Dużą rolę w obliczeniach odgrywają przekroje poprzeczne tych elementów. Przekroje te są figurami płaskimi.

Charakterystyka:

• Kształt przekroju - typowym przekrojem jest koło, kwadrat, prostokąt. Są to przekroje proste, niezłożone

• Wymiary przekroju - podajemy jeden wymiar w przypadku koła i kwadratu

• Pole przekroju

• Położenie środka ciężkości

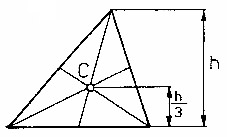
Środek ciężkości C trójkąta leży na przecięciu się jego środkowych

• Moment statyczny figury płaskiej (przekroju)

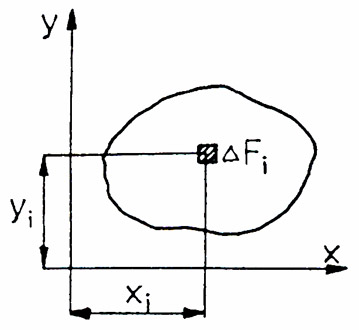
Moment statyczny figury płaskiej względem osi x:

[m³]

jeżeli
,
, to:

Wykazać, że S_x=0 jeżeli oś x jest osią centralną czyli przechodzącą przez środek ciężkości figury.

• Moment bezwładności figury płaskiej względem osi (oś leżąca w płaszczyźnie tej figury)

[m⁴]

Moment bezwładności figury płaskiej ( ......... moment bezwładności) jest równy sumie iloczynów pól elementarnych i kwadratów odległości tych pól od tej osi

Jeżeli

,
to:

ZAD. Dany jest prostokąt
. Wyprowadzić wzór na moment bezwładności tego prostokąta względem osi x przechodzącej przez jego podstawę

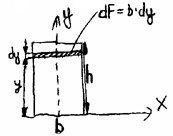
• Moment bezwładności figury płaskiej względem punktu (biegunowy moment bezwładności

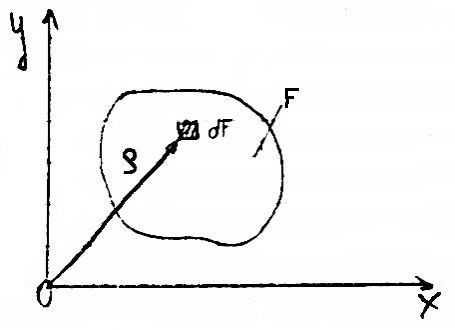
WYTRZYMAŁOŚĆ MATERIAŁÓW

Celem wytrzymałości materiałów jest określenie zależności pomiędzy obciążeniem ciał (elementów konstrukcyjnych) a wywołanymi przez te obciążenia odkształceniami i naprężeniami.

Zależności te są potrzebne do projektowania wytrzymałościowego elementów konstrukcyjnych.

Obciążenia: siły czynne działające na ciało, mogą to być :

siły skupione - skupione w jednym punkcie

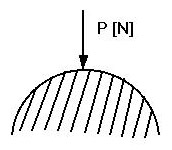
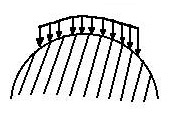
obciążenia ciągłe

q - obciążenie ciągłe liniowe [
]

P- obciążenie ciągle powierzchniowe, np. ciśnienie [
]

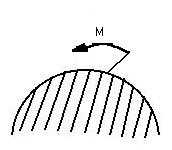
Moment skupiony - wynik działania pary sił

M - moment skupiony [
]

Obciążenie może mieć charakter: statyczny lub dynamiczny

Statyczny - obciążenie nie zmienne w czasie

Dynamiczny - wartość zmienna w czasie

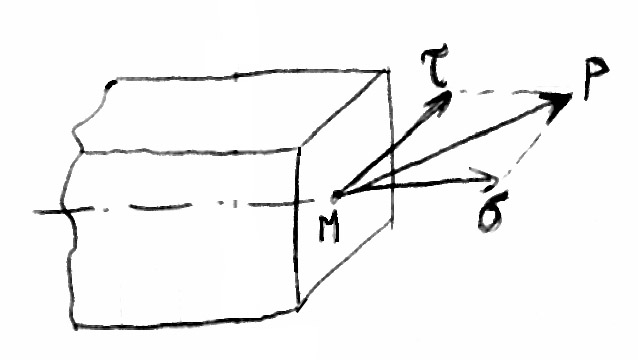
Naprężenia normalne i naprężenia styczne

Naprężenie w danym punkcie przekroju można rozłożyć na naprężenie normalne [
] i naprężenie styczne [
]. Naprężenie
jest prostopadłe do przekroju,
jest styczne do przekroju.

Założenia wytrzymałości materiałów:

• Materiały, z których wykonane są elementy konstrukcyjne są jednorodne

• Materiały są izotropowe, ich właściwości mechaniczne nie zależą od kierunku

(Uwaga - niektóre materiały konstrukcyjne są anizotropowe i to znacznie, np. drewno)

• Odkształcenia są tylko sprężyste

• Odkształcenia są bardzo małe
  

Podstawowe przypadki wytrzymałościowe czyli stany obciążeń pręta

1. 
   Osiowe rozciąganie pręta

2. 
   
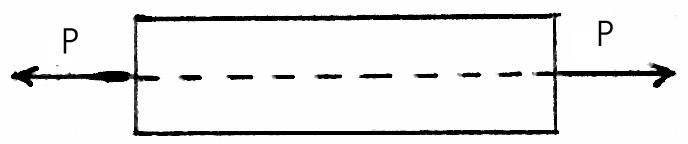
   Osiowe ściskanie pręta

3. 
   
   Czyste skręcanie pręta

4. 
   
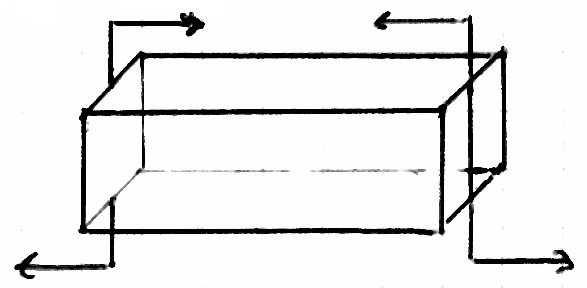
   Czyste skręcanie pręta

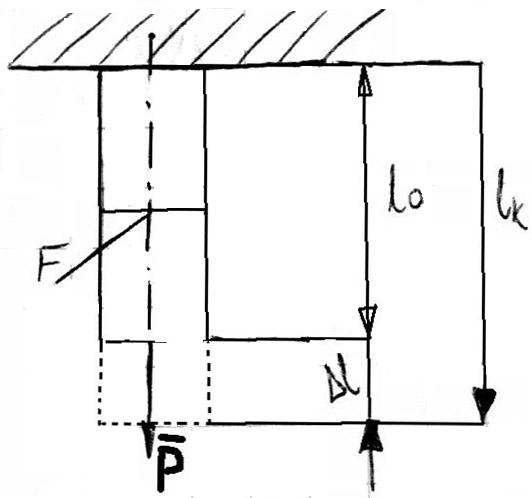
TEORIA OSIOWEGO ROZCIĄGANIA PRĘTA

Założenia: odkształcenia są tylko sprężyste

E - moduł sprężystości materiału (stała sprężystości) Younga

Przekształcam prawo Hooka:

Współczynnikiem proporcjonalności jest moduł Younga, naprężenie jest proporcjonalne do wydłużenia

PW: wykresy wytrzymałościowe dla: materiałów z wyraźną granicą plastyczności, dla materiałów bez wyraźnej granicy plastyczności, dla materiałów kruchych

• definicje wielkości (tzw. granic) występujących na wykresach wytrzymałościowych

(R_m - wytrzymałość materiału na rozciąganie
)

napięcie dopuszczające k_r
, n>1 (współczynnik bezpieczeństwa)

warunek wytrzymałościowy na rozciąganie

TYPY ZADAŃ

I typ	dane P, materiał (kr)
		oblicz: oblicz: wymiary przekroju (przy podanym kształcie przekroju)
	II typ	dane F, materiał (kr)
		oblicz: dopuszczalne wartości siły P
	II typ	dane P, F
		oblicz: dobrać materiał o niezbędnym kr

NAPRĘŻENIA TERMICZNE (CIEPLNE)

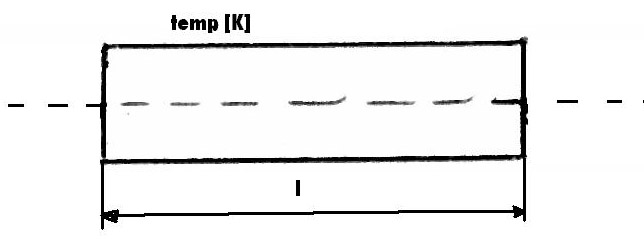
α - współczynnik rozszerzalności cieplnej

równanie zgodności odkształcenia

naprężenia cieplne

Naprężenia cieplne mogą występować w tzw. układach statycznie niewyznaczalnych, natomiast nie występują w układach statycznie wyznaczalnych.

PRAWO HOOKA DLA DWUKIERUNKOWEGO ROZCIĄGANIA

Odkształcenie wywołane naprężeniem
(odkształcenie jednostkowe)

odkształcenia wywołane naprężeniem

współczynnik Poissona

skrócenie jednostkowe w kierunku prostopadłym do rozciągania

I=

wydłużenie jednostkowe w kierunku rozciągania

Zgodnie z zasadą superpozycji:

Objętość ciała rozciąganego wzrasta

-liczba mała

-liczba mała wyższego rzędu (II-go rzędu)

-stała sprężystości materiału (2-ga obok E)

Jeżeli
=0,5 to objętość rozciąganego ciała nie wzrasta

skrócenie(przewężenie) jednostkowe w kierunku prostopadłym do rozciągania

=

wydłużenie jednostkowe w kierunku rozciągania

x - kierunek rozciągania

Jakie wartości może przyjmować współczynnik Poissona
dla ciał izotropowych

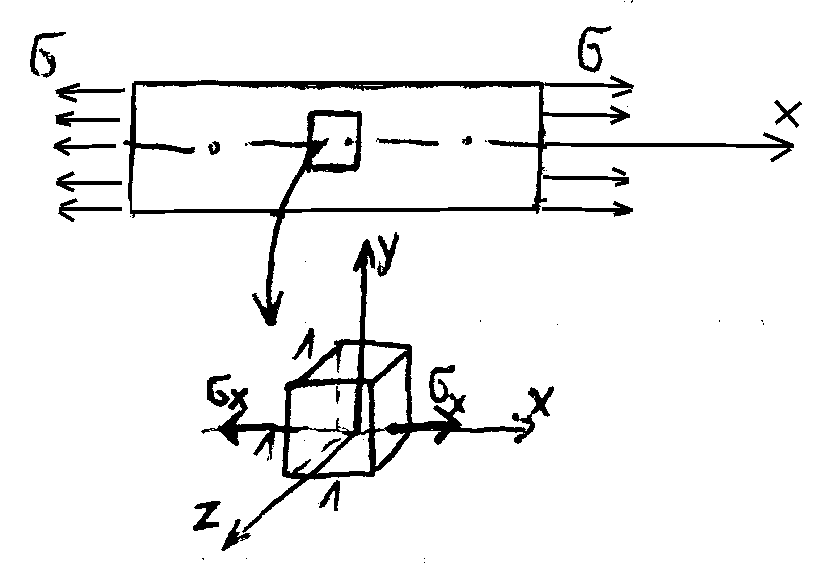
Dany jest pręt rozciągany osiowo

Wymiary kostki elementarnej przed odkształceniem: 1,1,1

Wymiary kostki elementarnej po

odkształceniu:

Objętość kostki elementarnej przed odkształceniem: V_P=1³

Objętość kostki elementarnej po

odkształceniu:

Zginanie pręta zachodzi wtedy gdy działają na niego siły prostopadłe do jego osi. Pręt zginany nazywamy belką.

Dwa podstawowe schematy belek:

• belka podporowa (wolno podparta)

• belka wspornikowa (jednostronnie utwierdzona)

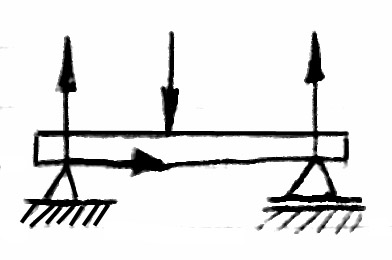
Rozpatrujemy zginanie płaskie tzn. siły obciążające belkę działają w jednej płaszczyźnie, która zawiera oś pręta (belki) i jedną z głównych ( ) osi bezwładności przekroju.

Siły wewnętrzne w belce - w belkach mogą występować następujące siły wewnętrzne (określone do poszczególnych przekrojów poprzecznych belki:

1. Moment zginający M_g

2. siła tnąca (poprzeczna) T

3. 
   siła podłużna N

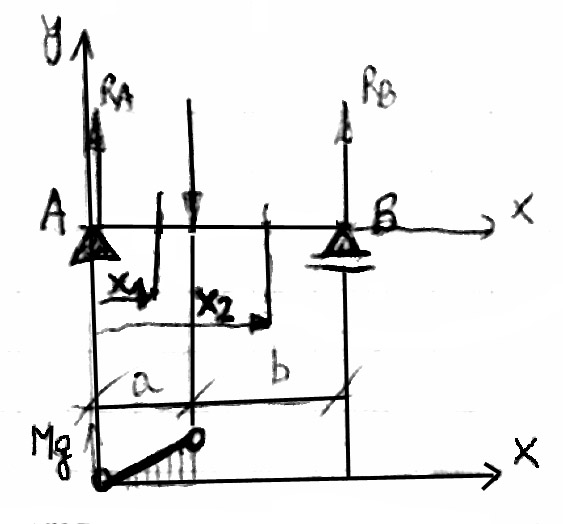
(a)

(b)

(c)

dla x=0 , M_g=0

dla x=a , M_g=R_Aa

Czyste zginanie

Zależność między M_g i T

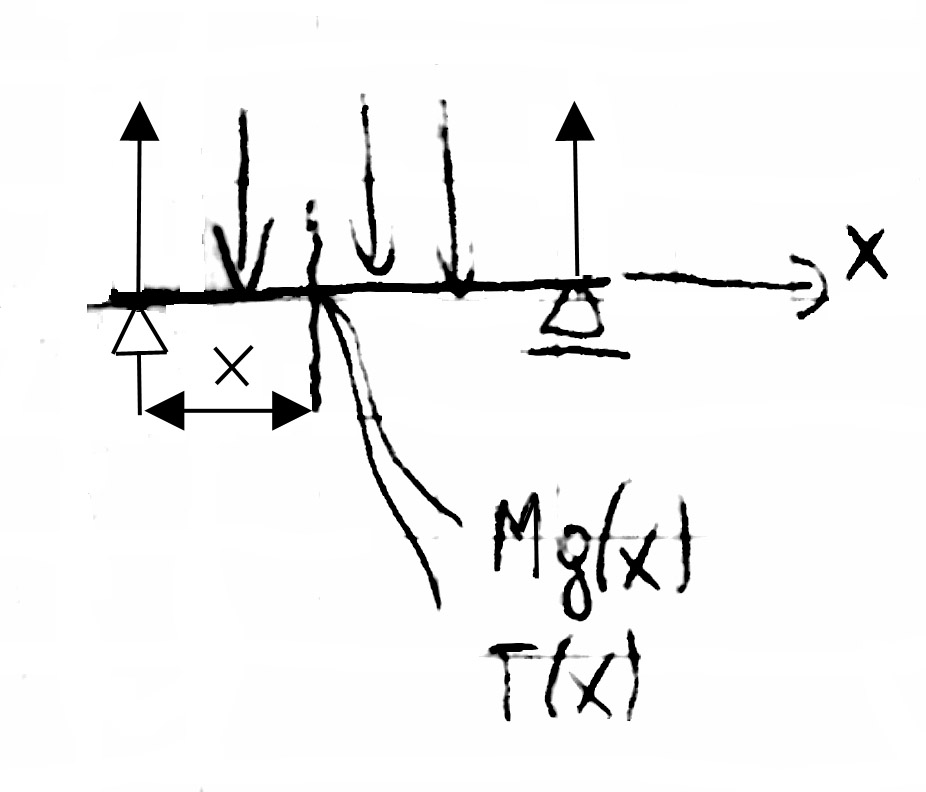
siła tnąca w belce = pierwszej pochodnej momentu tnącego względem osi l

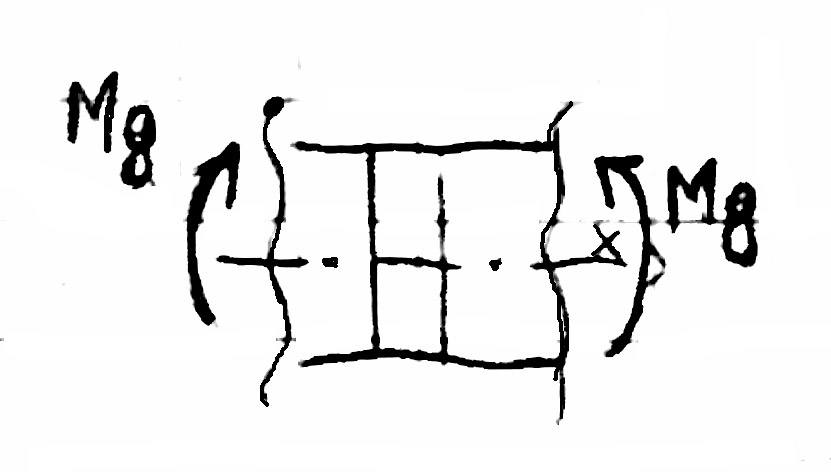
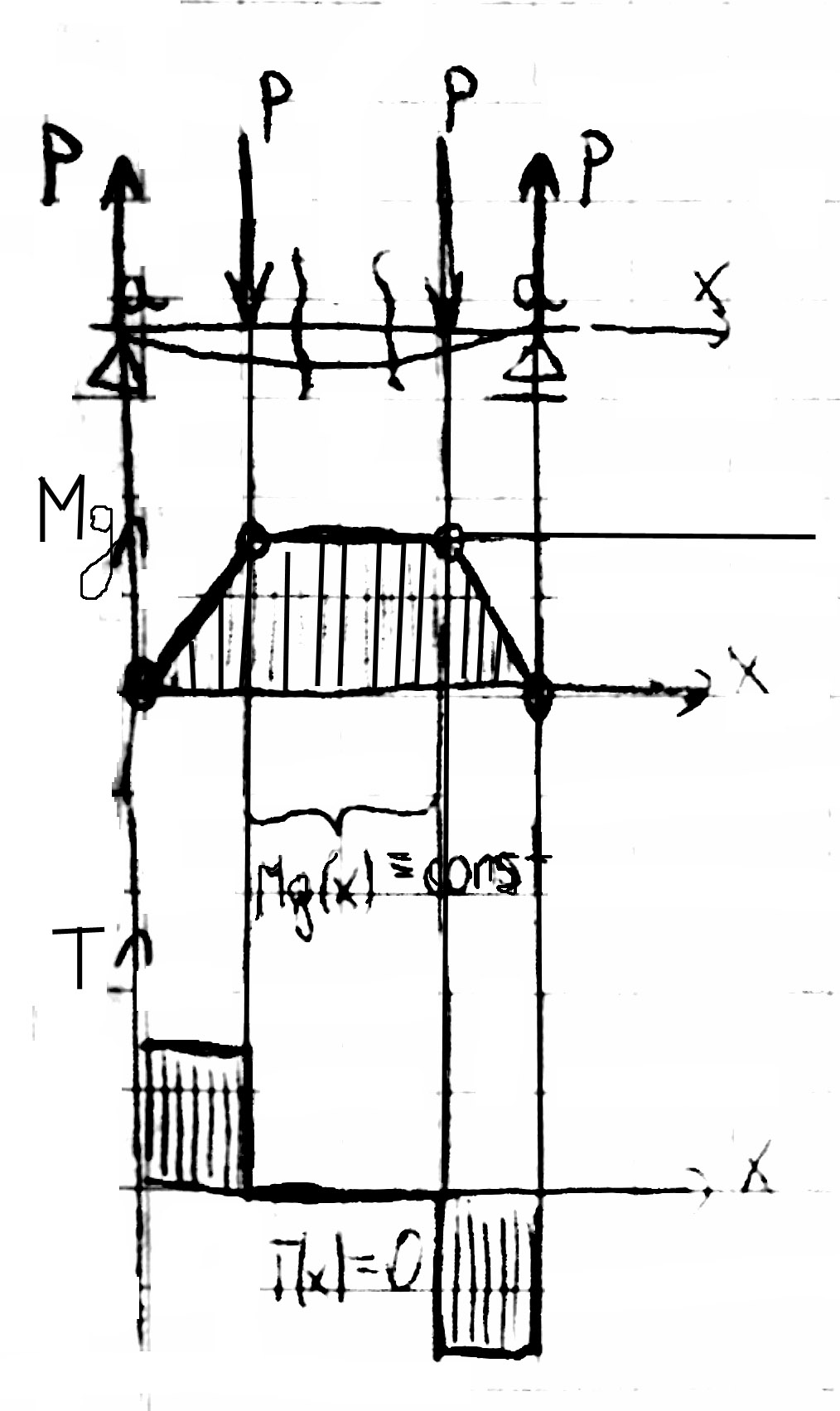
Czyste zginanie - występuje wtedy gdy w danym odcinku belki
, wtedy:
, a więc nie występuje ścinanie.

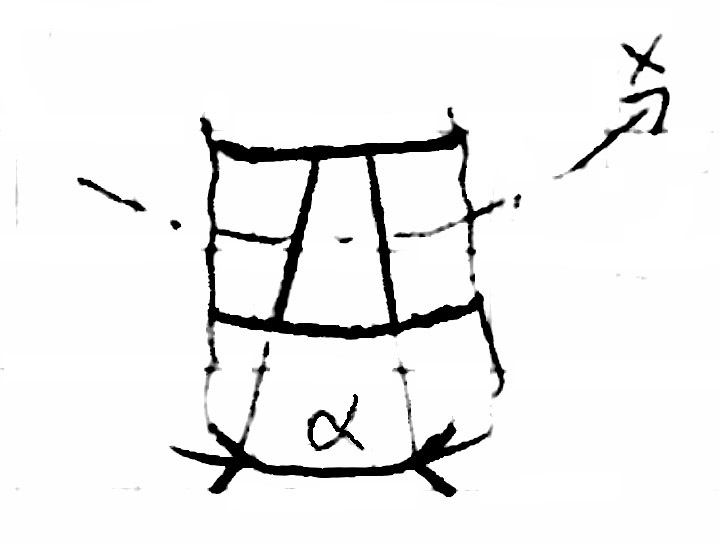
I Hipoteza płaskich przekrojów - przy czystym zginaniu przekroje belki płaskie obracając się względem siebie o pewne kąty.

II Hipoteza pracy włókien belki - Włókna belki nie naciskają na siebie, są tylko ściskane lub rozciągane.

Warstwa obojętna to warstwa włókien, które nie są ani rozciągane ani ściskane. Na ogół warstwa ta zawiera oś belki.

Naprężenia przy zginaniu

Oś obojętna przekroju - to oś wynikająca z przecięcia się osi obojętnej z danym przekrojem

- naprężenie

I_z - moment bezwładności względem osi obojętnej z przekroju

y - odległość danego punktu od osi obojętnej

W_z = wskaźnik wytrzymałości przekroju

Przykład: Oblicz W_z dla pręta

Warunek wytrzymałościowy na zginanie

Rozciąganie P_max - max. siła potrzebna do rozerwania pręta

F - pole przekroju pręta

R_m - wytrzymałość na rozciąganie

- czyste zginanie

- zginanie ze ścinaniem (zginanie poprzeczne)

NOŚNOŚĆ BELKI - to takie jej największe obciążenie przy , którym naprężenia max są równe naprężeniom dopuszczalnym na zginanie dla materiału belki.

- nośność belki

Problem: belka o przekroju prostokątnym
, h > b podparta jest na dwóch podporach i obciążona siłą skupioną P w połowie jej długości l. Najpierw belka ułożona jest na sztorc, następnie na płask. Porównać nośność belki przy tych dwóch ułożeniach jeżeli dane są : b, h, l, k_g .

Wyprowadzamy iloraz (stosunek) nośności

Nośność belki ułożonej na sztorc jest większa od belki ułożonej na płask tyle razy, ile razy wysokość przekroju h jest większa od wysokości przekroju b.

LINIA UGIĘCIA BELKI

y=y(x) równanie linii ugięcia belki

y - ugięcie
- kąt ugięcia

dla małych kątów

y_max=f strzałka ugięcia

warunek sztywności przy zginaniu

- promień krzywizny

- krzywizna

równanie różniczkowe linii ugięcia belki

Problem : Dana jest belka wspornikowa o długości l, obciążona na swobodnym końcu siłą P. Wyznaczyć równanie ugięcia belki oraz f i
.

moment zginający w przekroju belki określony współrzędną x

równanie różniczkowe linii ugięcia belki:

całkujemy równanie różniczkowe po raz pierwszy:

C₁ - stała całkowania

stałą C₁ wyznaczamy z I warunku brzegowego

dla x=l ,

całkujemy równanie po raz drugi:

stałą C₂ wyznaczamy z II warunku brzegowego

dla x=l , y=0

ostatecznie równanie linii ugięcia ma postać:

Mg=const czyste zginanie

siła tnąca Naprężenia są zwrócone w prawo i lewo, gdyż włókna belki górne są ściskane, a dolne rozciągane

f- strzałka ugięcia

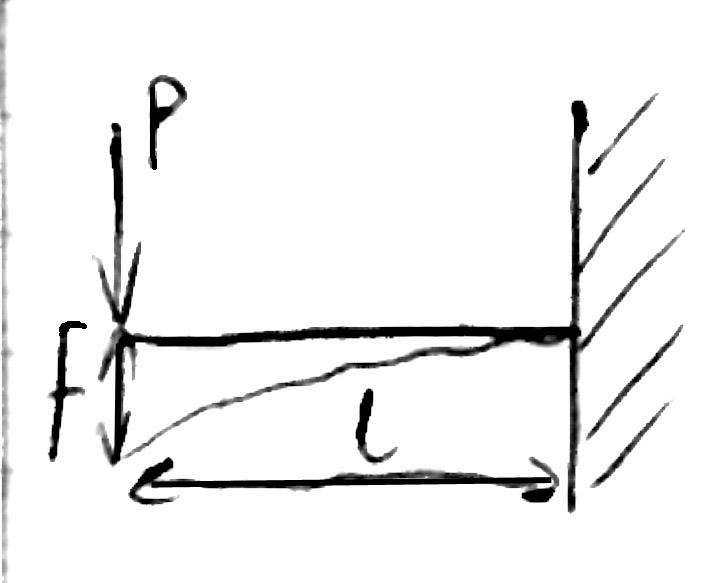
belka wspornikowa

- sztywność zginania

Im większa jest sztywność zginania tym mniejsze jest ugięcie belki

Problem: belka o przekroju prostokątnym
, h > b podparta jest na dwóch podporach i obciążona siłą skupioną P w połowie jej długości l. Najpierw belka ułożona jest na sztorc, następnie na płask. Porównać ugięcia belki przy tych dwóch ułożeniach przy założeniu działania siły o tej samej wartości P

dla belki ułożonej na płask	dla belki ułożonej na sztorc

Ugięcie belki ustawiionej na sztorc jest mniejsze niż belki ustawionej na płask tyle razy ile wynosi kwadrat ilorazu wysokości / szerokości przekroju belek.

Gdy pręt rozciągamy to kształt nie jest istotny.

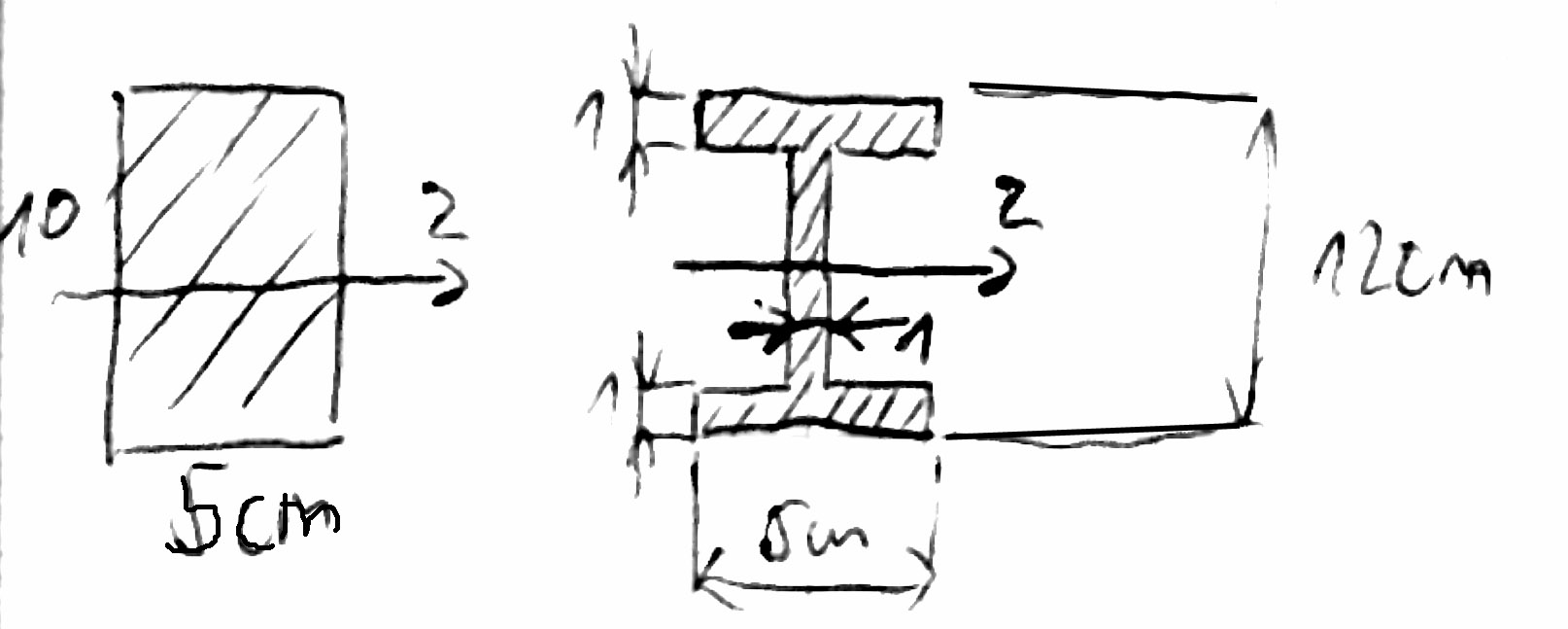
Problem: Dane są belki : I- o przekroju prostokątnym 5 na 10 cm

II- o przekroju dwuteowym, jak na rysunku.

Porównać nośność, sztywność, oraz ciężar obu belek przy założeniu, że mają one jednakową długość i są wykonane z tego samego materiału

ciężar

Dwuteownik jest lepszym przekrojem niż prostokąt, gdyż przy większej oszczędności materiału (czyli zysk na ciężarze) uzyskuje się nieco tylko gorsze parametry od przekroju prostokątnego.

W przekroju poprzecznym występuje tylko naprężenia normalne
, które są rozłożone równomiernie w całym przekroju

W przekroju poprzecznym występuje tylko naprężenia normalne
, które są rozłożone równomiernie w całym przekroju

Występują tylko naprężenia styczne
,różne w różnych kierunkach

W przekrojach poprzecznych pręta występują tylko naprężenia normalne
, różne, w różnych punktach przekroju

Prawo Hooka

odkształcenie jest proporcjonalne do odkształcenia

Wydłużenie względne (jednostkowe)

Układ statycznie wyznaczalny

Układ statycznie niewyznaczalny

prawo Hooka dla dwukierunkowego rozciągania

dla

linia ugięcia belki (ugięta oś belki)

M_g - moment zginający

E - moduł sprężystości belki

I_z - moment bezwładności belki

---