1

Przedmiot:

Mechanika

Formy zajęć: wykład - 30 godz./sem.

ćwiczenia - 15 godz./sem.

Prowadzący: dr inż. Radosław Machlarz, p. 110

mgr inż. Wojciech Zieliński, p. 113

Warunki zaliczenia:

wykład: egzamin

ćwiczenia: kolokwium pisemne

2

Literatura

1. Kozak B.: Mechanika techniczna, WSiP

2. Leyko J.:

Mechanika ogólna, PWN

3.

Niezgodziński T.: Mechanika ogólna, PWN

4. Misiak J.:

Zadania z mechaniki ogólnej, WNT

5. Ostwald M.:

Podstawy wytrzymałości materiałów,

Wydawnictwo Politechniki Poznańskiej

6. Ostwald M.:

Wytrzymałość materiałów. Zbiór zadań,

Wydawnictwo Politechniki Poznańskiej

3

statyka

kinematyka

dynamika

mechanika

ogólna

teoria

sprężystości

teoria

plastyczności

wytrzymałość

materiałów

mechanika

ciał odkształcalnych

hydromechanika

aeromechanika

mechanika

płynów

Mechanika

Działy mechaniki

4

Podstawowe pojęcia mechaniki

Uproszczone modele ciał rzeczywistych:

•

Punkt materialny

– punkt geometryczny obdarzony masą,

•

Układ punktów materialnych – zbiór punktów materialnych

zachowujących odległości,

•

Ciało doskonale sztywne – ciało nie podlegające

odkształceniom pod wpływem działania sił.

5

Podstawowe prawa mechaniki

–

prawa Newtona

sformułowane w 1687r., odnoszące się do punktu materialnego

6

7

8

Jednostki siły i masy

Masa a ciężar ciała

9

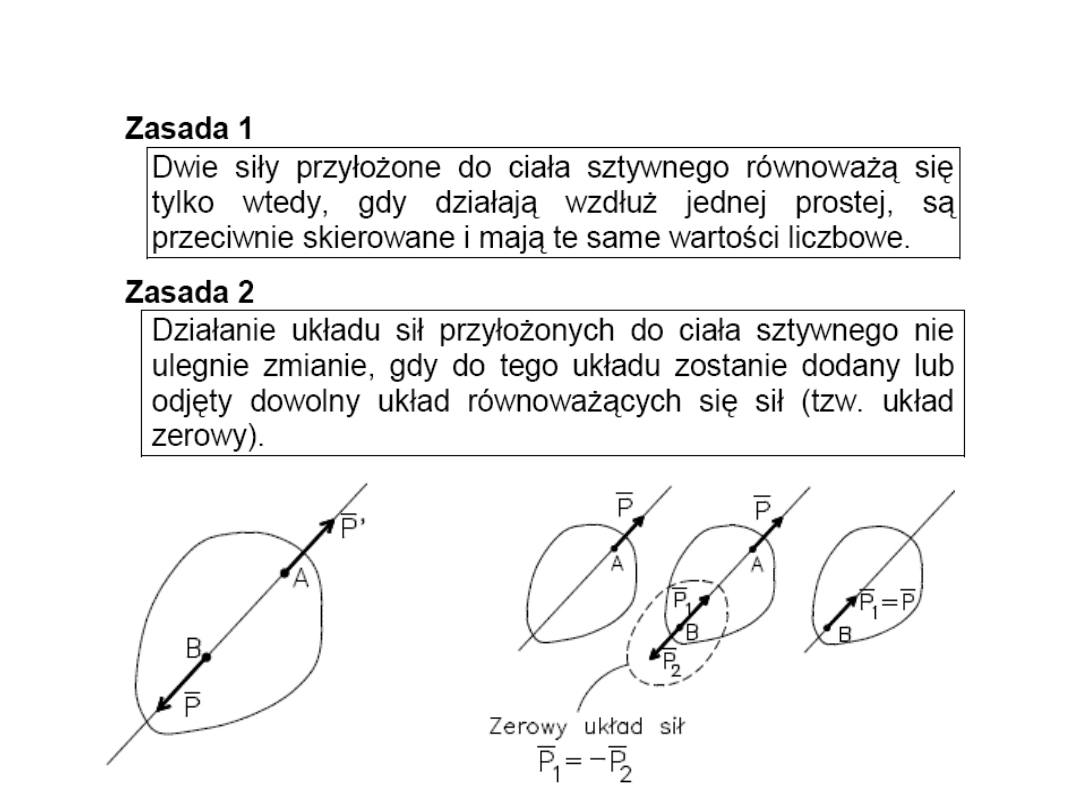
Zasady statyki

10

11

12

Ciało nieswobodne można rozpatrywać jako swobodne
podlegające działaniu sił czynnych oraz sił biernych –
reakcji więzów.

Więzy – ograniczenia ruchu nakładane przez inne ciała.

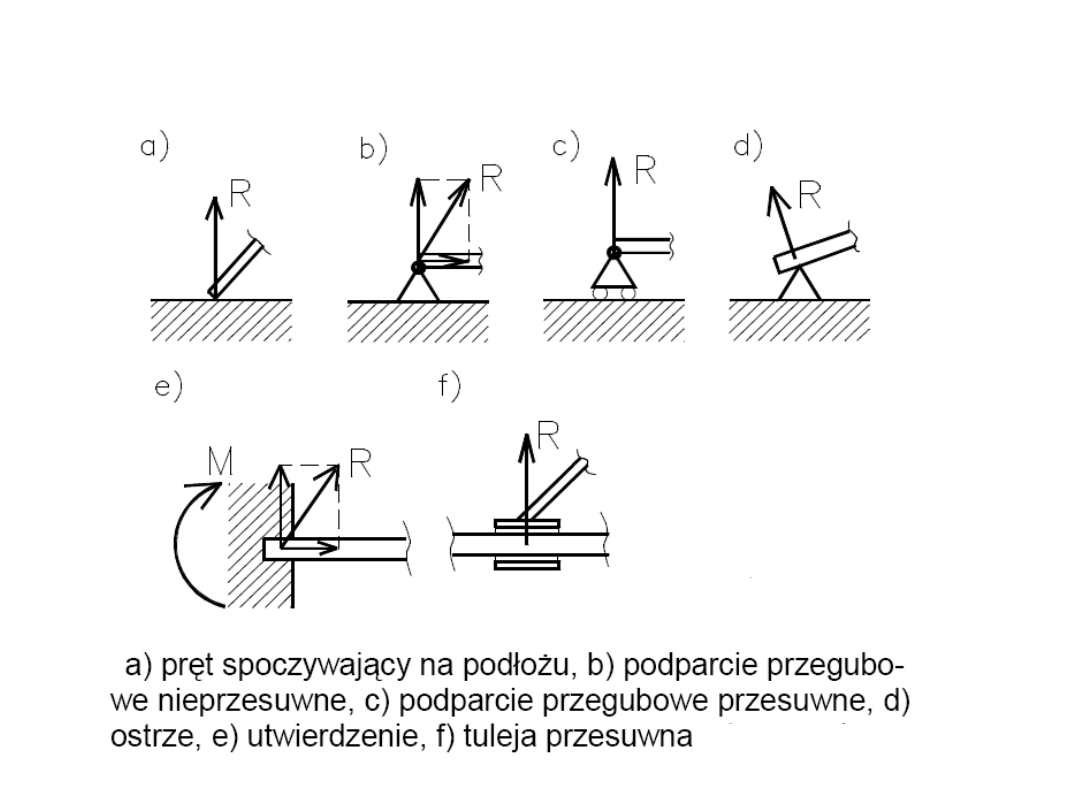
13

Przykłady więzów i ich reakcje

14

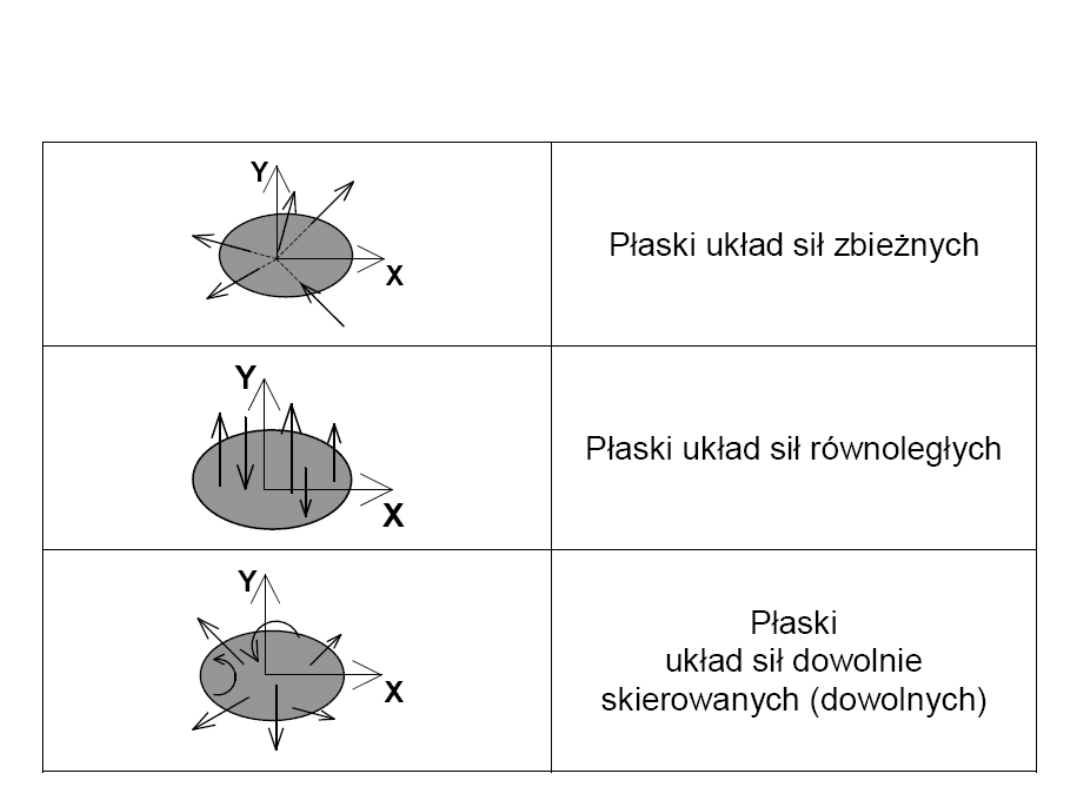
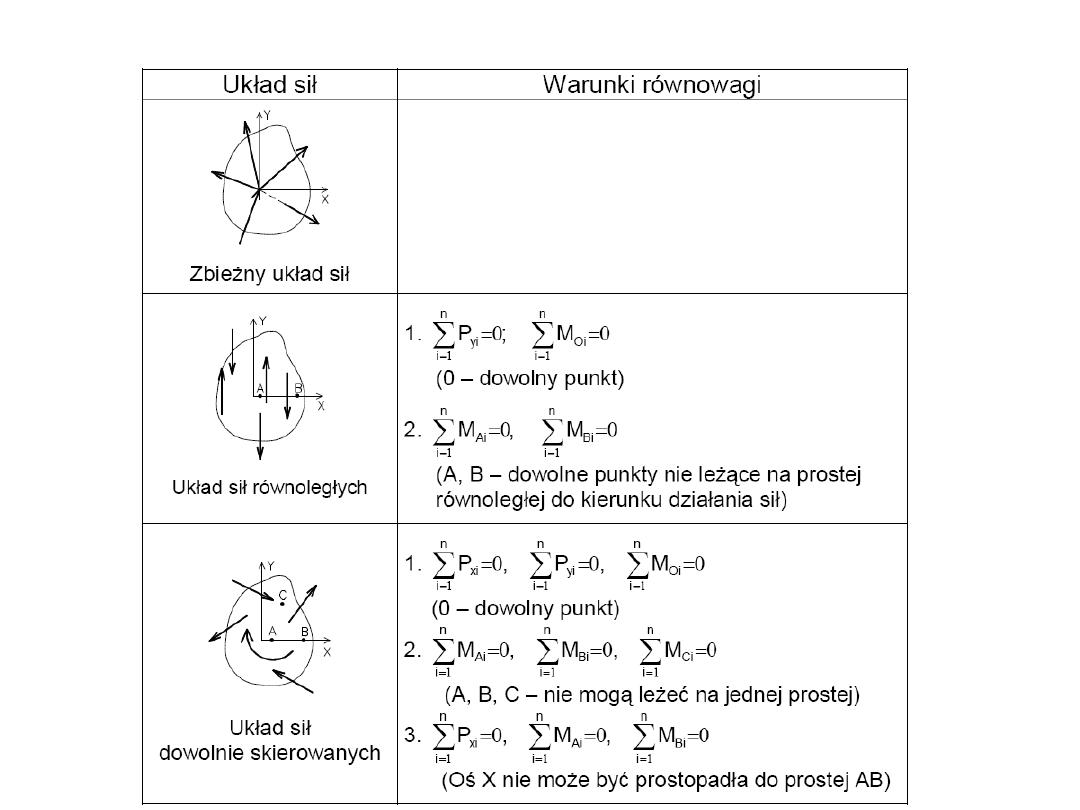
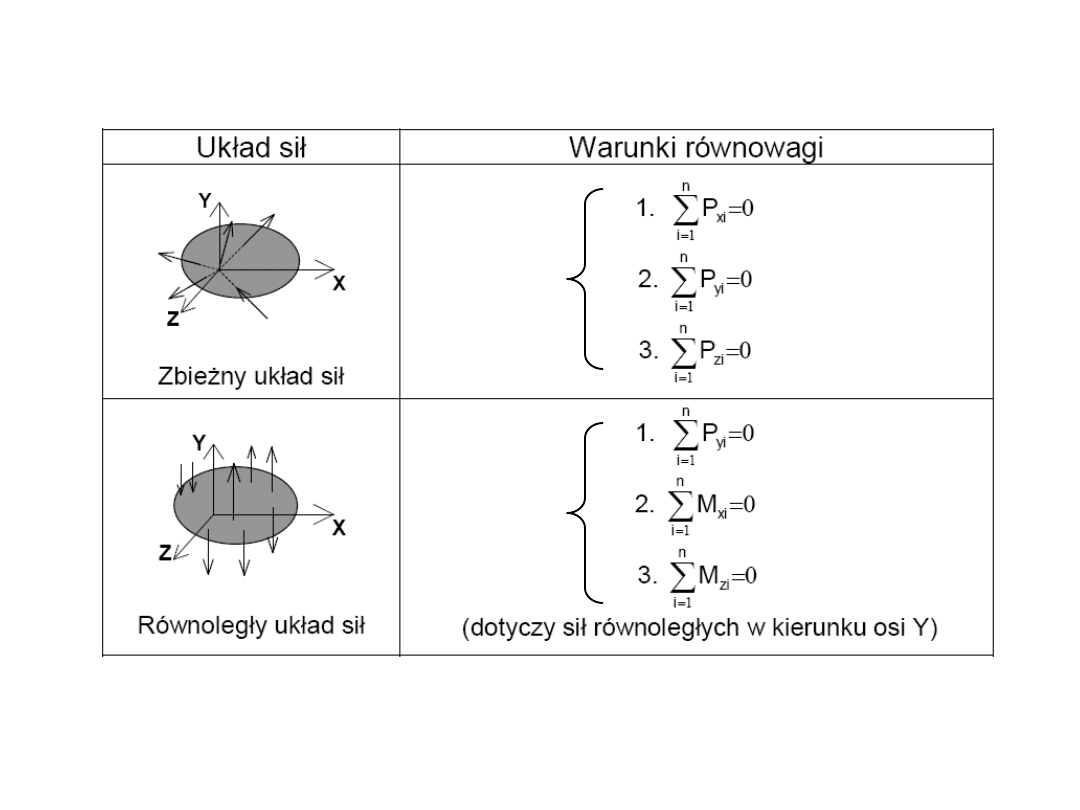
Płaskie układy sił

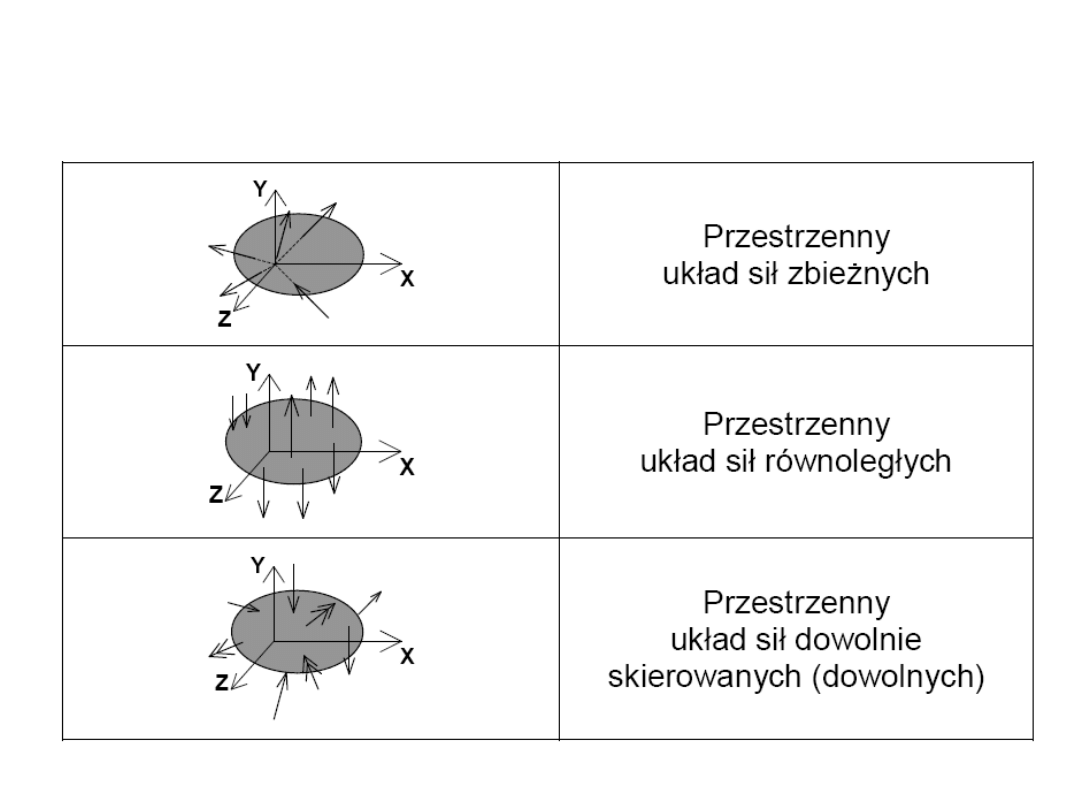
15

Przestrzenne układy sił

16

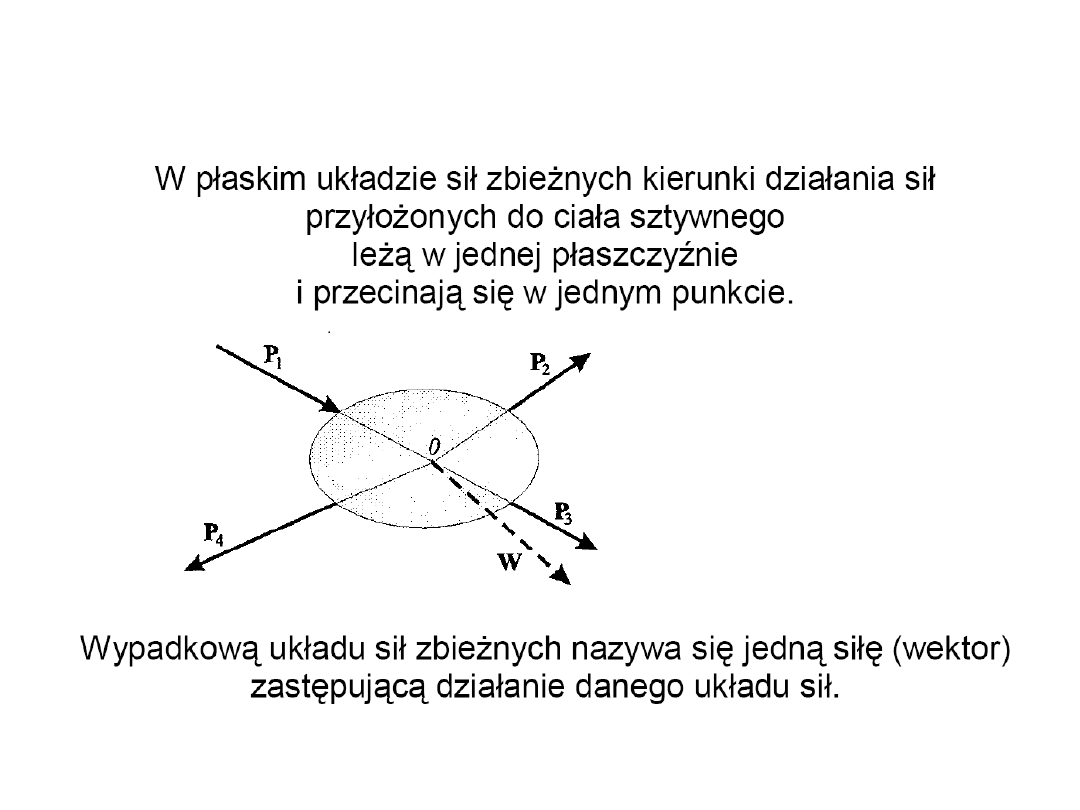
Płaski układ sił

zbieżnych

18

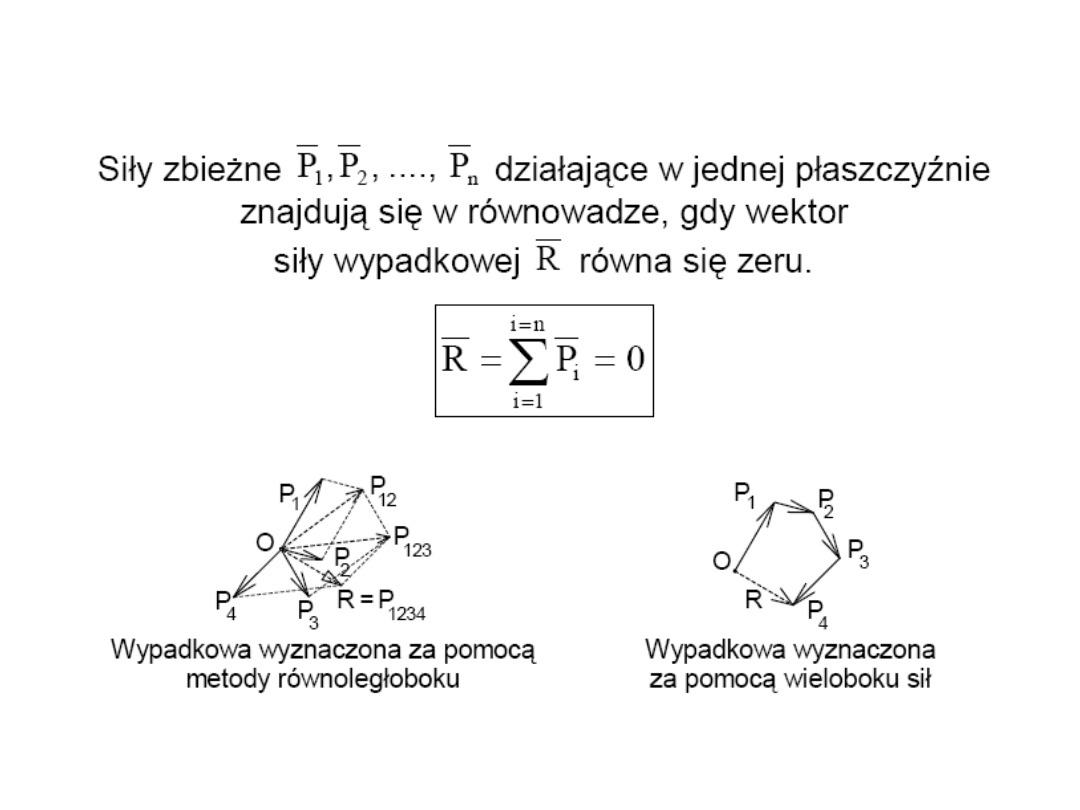
Warunek równowagi płaskiego zbieżnego układu sił

19

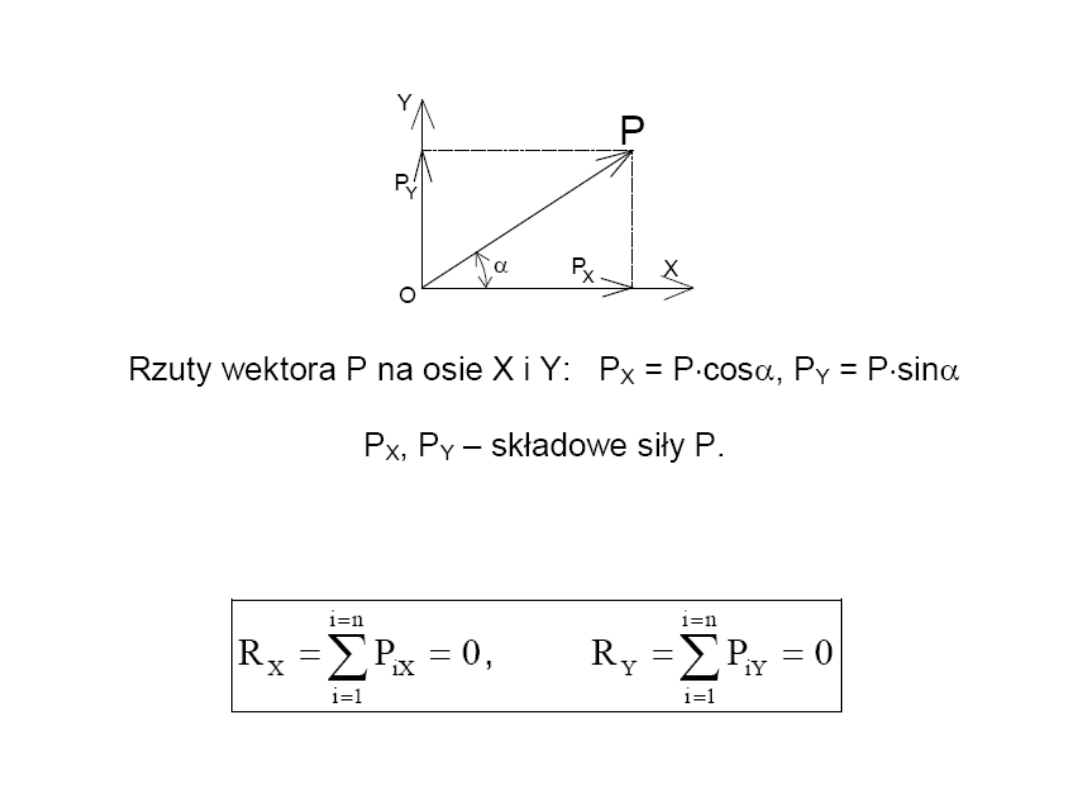
Analityczne wyznaczanie siły wypadkowej

Równania równowagi płaskiego układu sił zbieżnych

w zapisie analitycznym

20

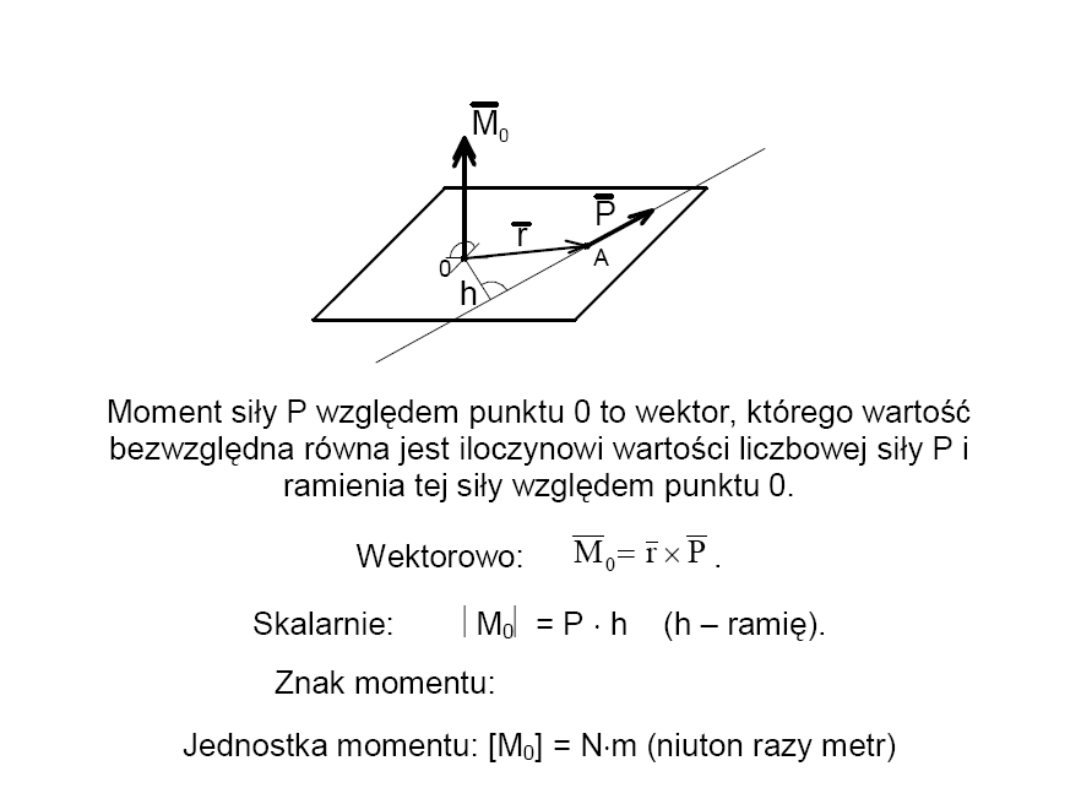
Moment siły względem punktu

reguła śruby prawoskrętnej

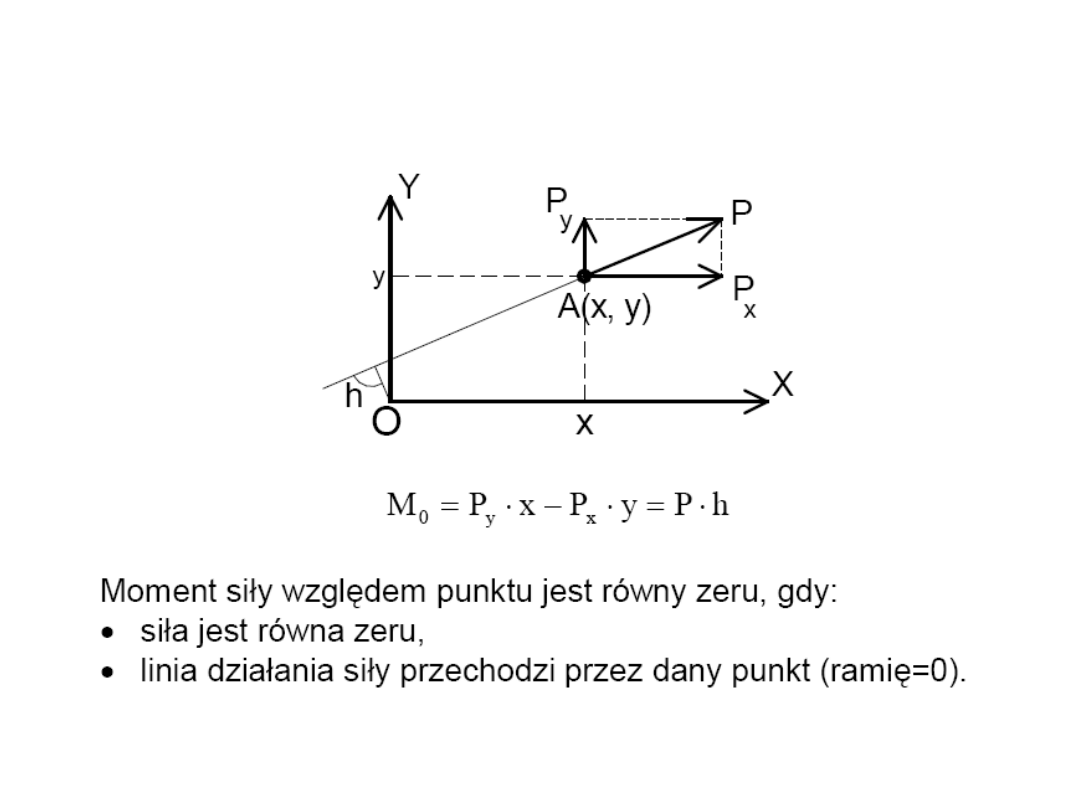
21

Analityczne wyznaczanie momentu

22

Płaskie układy sił równoległych

Płaski układ sił równoległych o tych samych zwrotach

23

Płaski układ sił równoległych o przeciwnych zwrotach

Płaskie układy sił równoległych

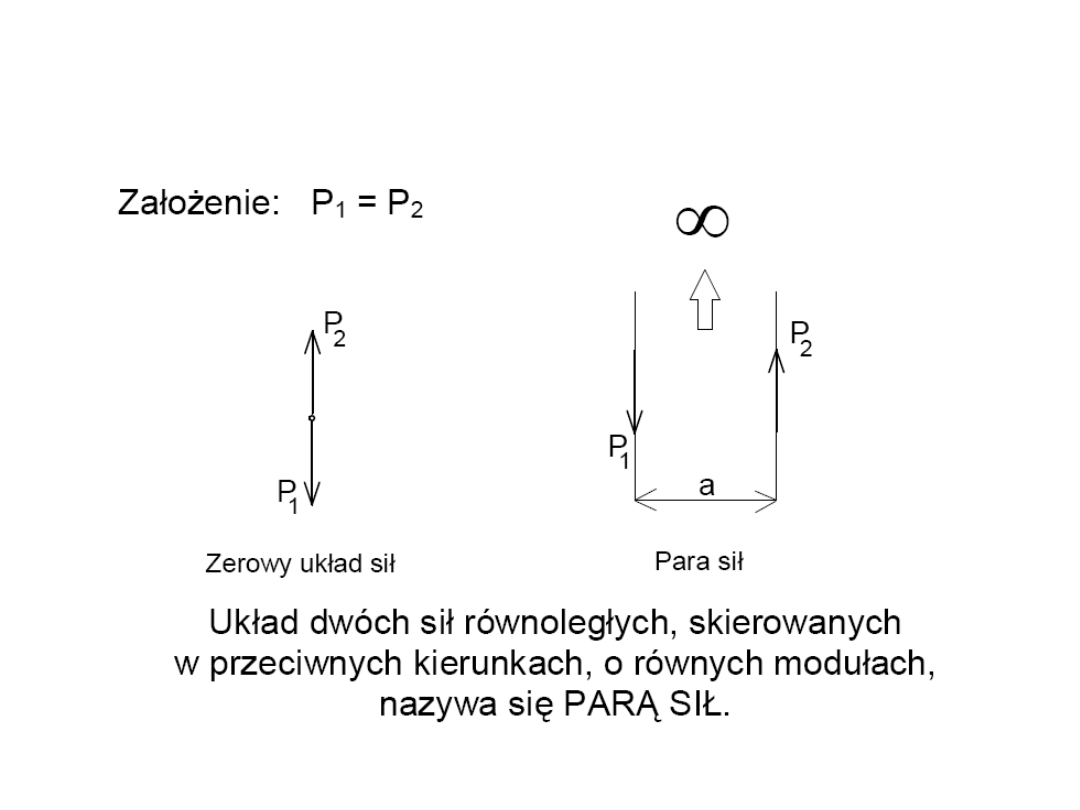
24

Para sił

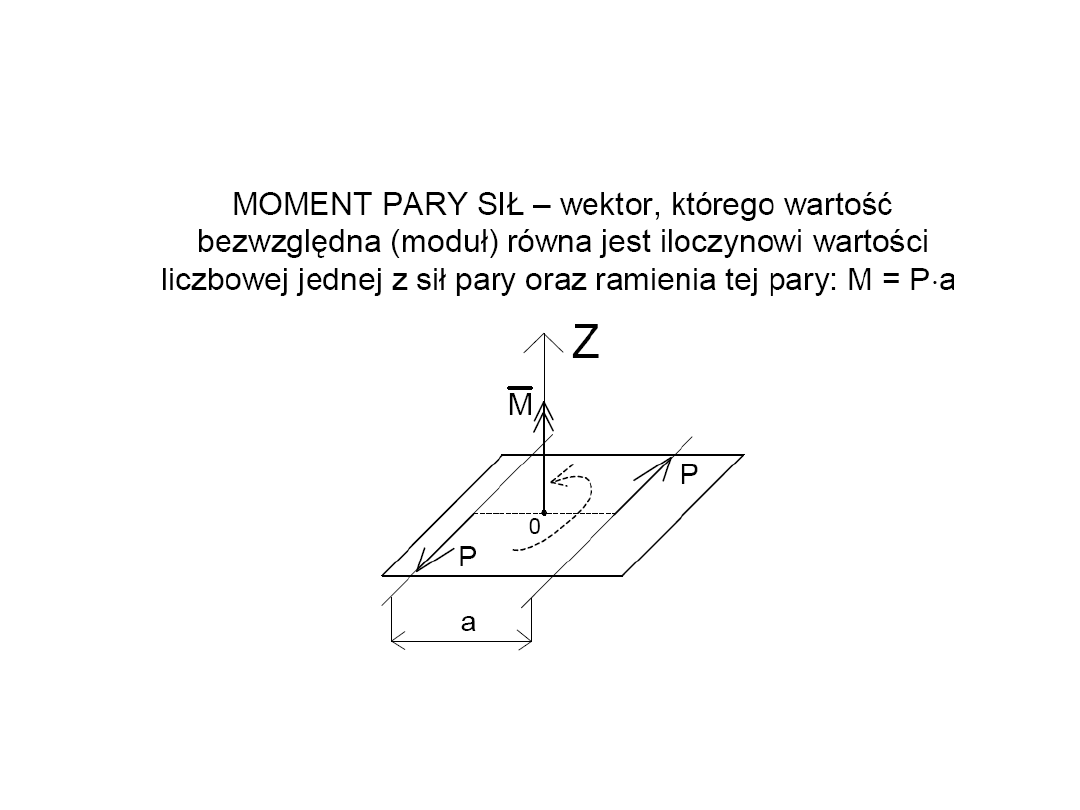
25

Moment pary sił

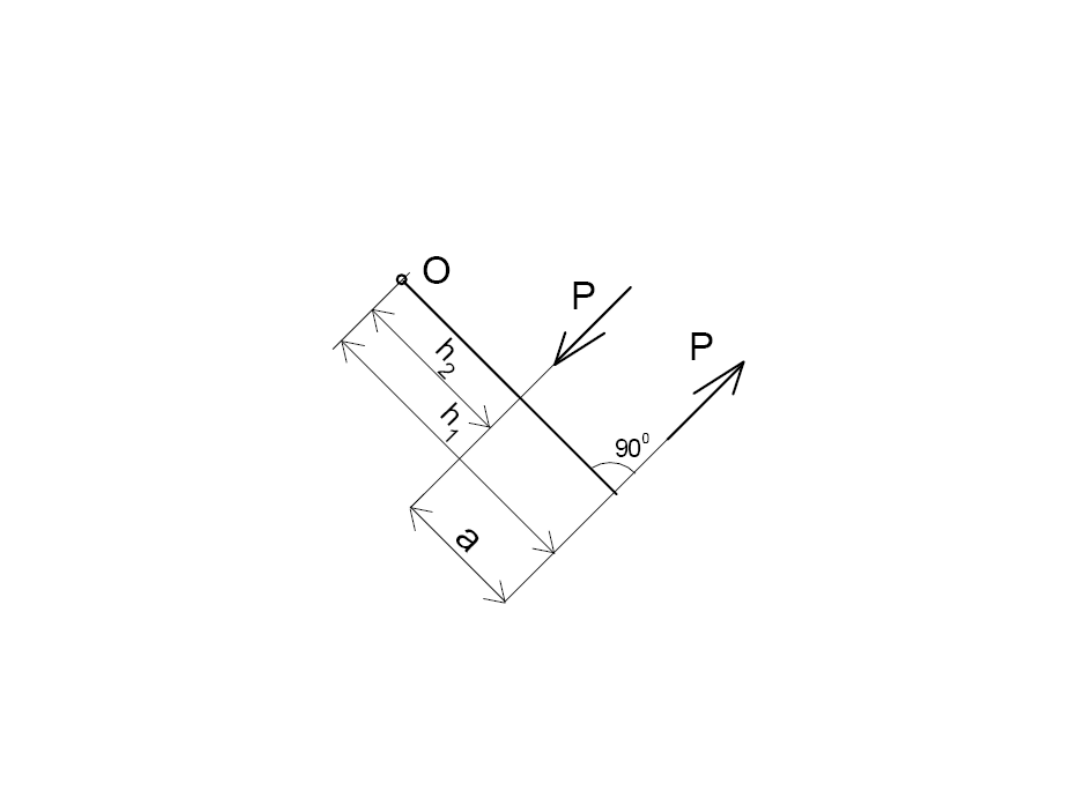
26

Moment sił tworzących parę

względem dowolnego punktu

Suma momentów sił tworzących parę względem

dowolnego punktu równa jest momentowi danej pary sił

27

Gdy na ciało sztywne działa n par sił leżących w jednej

płaszczyźnie, to pary te można zastąpić parą wypadkową o

momencie równym sumie momentów poszczególnych par:







n

i

i

M

M

1

0

1







n

i

i

M

Warunek równowagi par sił działających w jednej

płaszczyźnie

28

Warunki równowagi płaskich układów sił
























n

i

yi

n

i

xi

P

P

1

1

0

0

29

Warunki równowagi przestrzennych układów sił

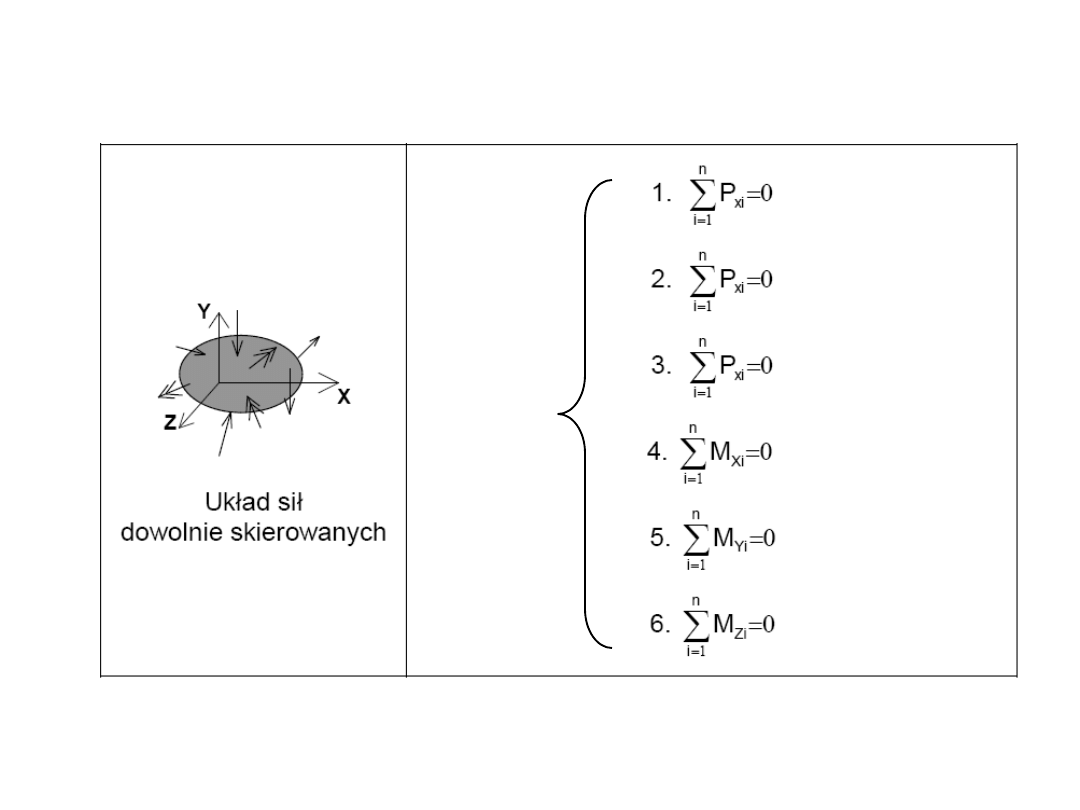
30

Warunki równowagi przestrzennych układów sił

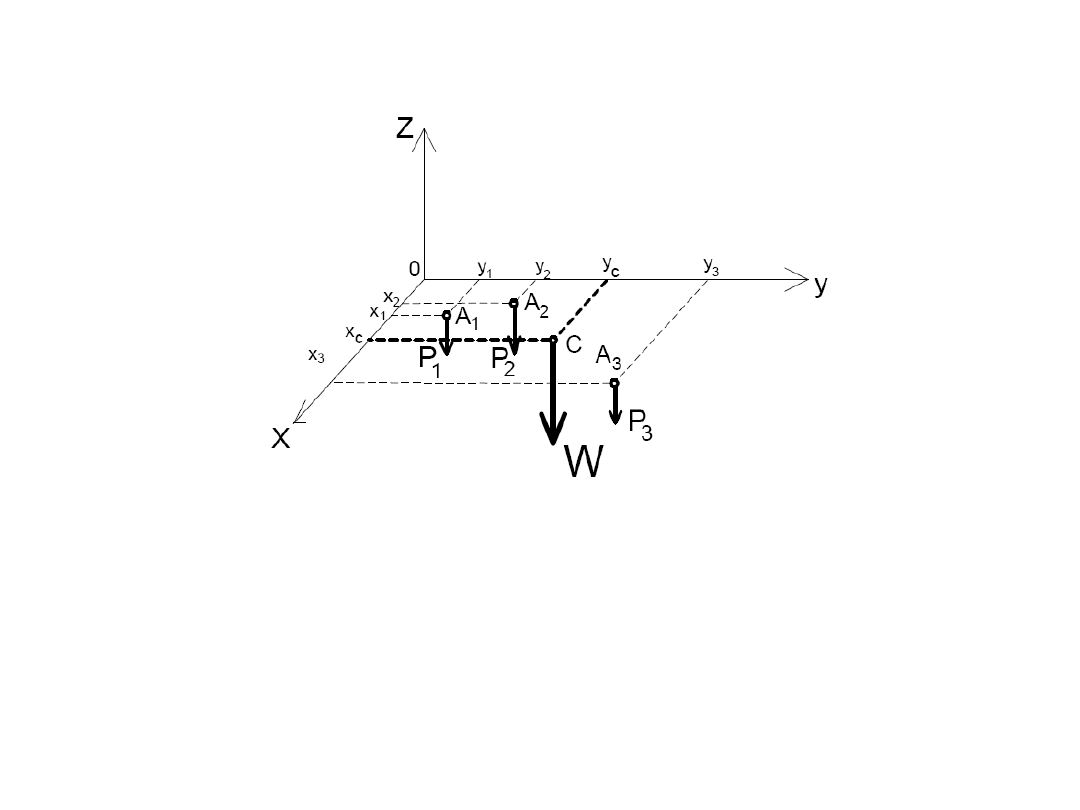
31

Środek przestrzennego układu sił równoległych

Siła wypadkowa W dowolnej liczby n sił równoległych do osi
z

, przyłożonych w punktach A

i

(x

i

,y

i

,0) wynosi:







n

i

i

P

W

1

32

Punkt przyłożenia siły W musi być taki, aby moment tej siły
względem danej osi był równy sumie momentów
poszczególnych sił składowych:











n

i

i

i

c

x

P

x

W

1











n

i

i

i

c

y

P

y

W

1

Współrzędne punktu przyłożenia siły W (środek sił
równoległych, środek ciężkości):













n

i

i

n

i

i

i

c

P

x

P

x

1

1













n

i

i

n

i

i

i

c

P

y

P

y

1

1

33

Środek ciężkości

34

Środek ciężkości bryły

Jeżeli:
dV

i

– objętość dostatecznie małego elementu bryły,



i

– ciężar właściwy danego elementu,

x

i

, y

i

, z

i

– współrzędne danego elementu,

to współrzędne środka ciężkości bryły:











n

i

i

n

i

i

i

c

dV

dV

x

x

1

1















n

i

i

n

i

i

i

c

dV

dV

y

y

1

1















n

i

i

n

i

i

i

c

dV

dV

z

z

1

1





Po przejściu do granicy:

G

xdV

x

V

c







G

ydV

y

V

c







G

zdV

z

V

c











V

dV

G



-

całkowity ciężar bryły.

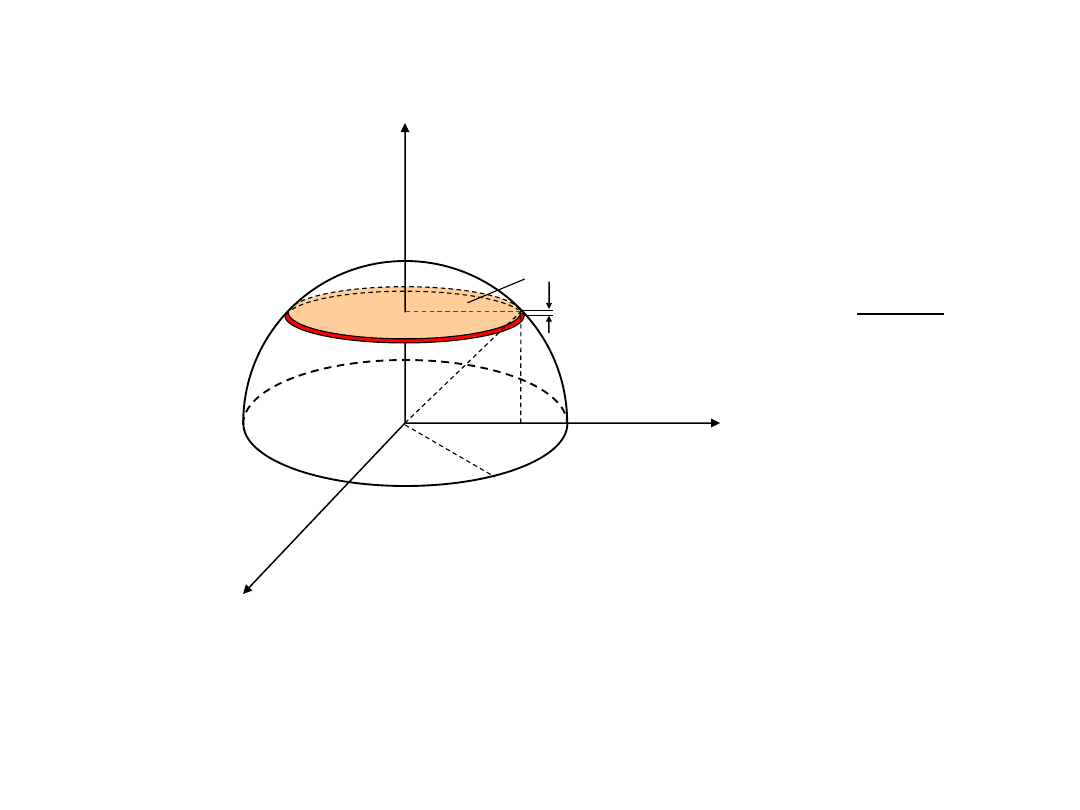
35

Przykład 1: Znaleźć położenie środka ciężkości jednorodnej półkuli o
promieniu r.

z

r

y

r

y

z

x

dz

dV

V

zdV

z

V

c





0





c

c

y

x

Przykład 2: Znaleźć położenie środka ciężkości połowy jednorodnej
powierzchni kulistej o promieniu r.

36

Środek ciężkości figury płaskiej

Jeżeli jednorodna figura płaska leży w płaszczyźnie x-y, to:

F

xdF

x

F

c





F

ydF

y

F

c









F

y

xdF

S

-

moment statyczny względem osi y,





F

x

ydF

S

-

moment statyczny względem osi x.

F

– pole powierzchni figury.

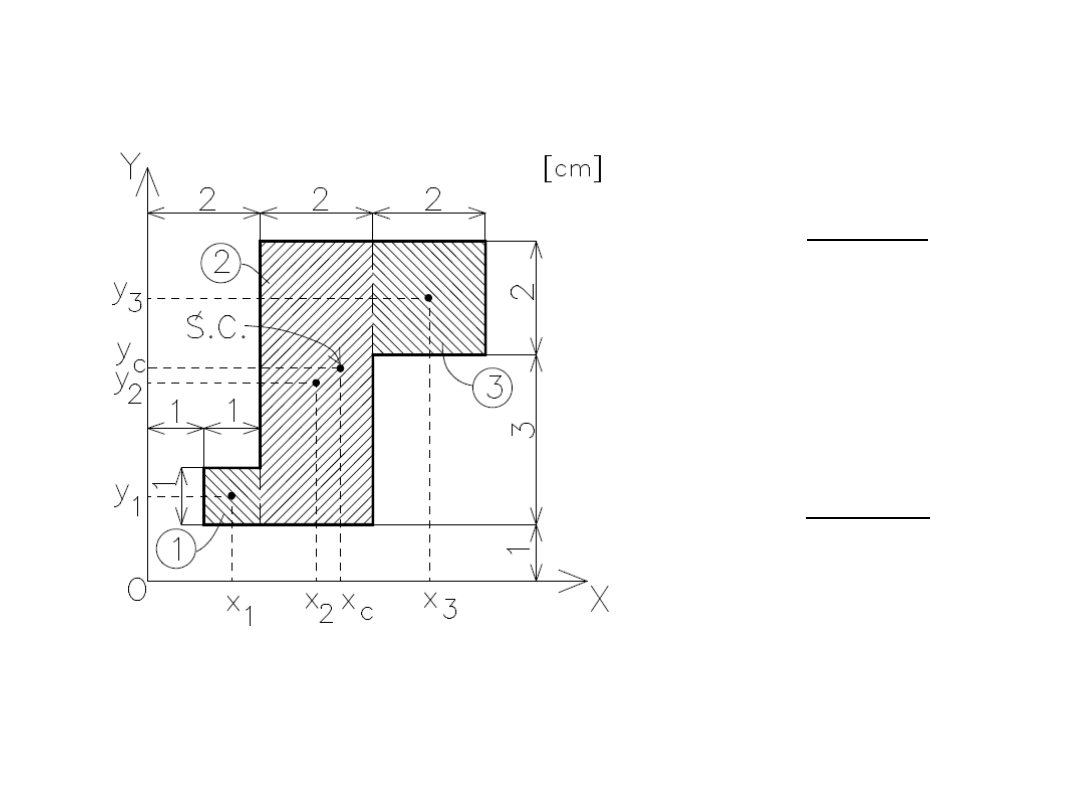
37

Przykład 3: Znaleźć środek ciężkości danej figury płaskiej.











3

1

3

1

i

i

i

i

i

c

F

F

x

x











3

1

3

1

i

i

i

i

i

c

F

F

y

y

38

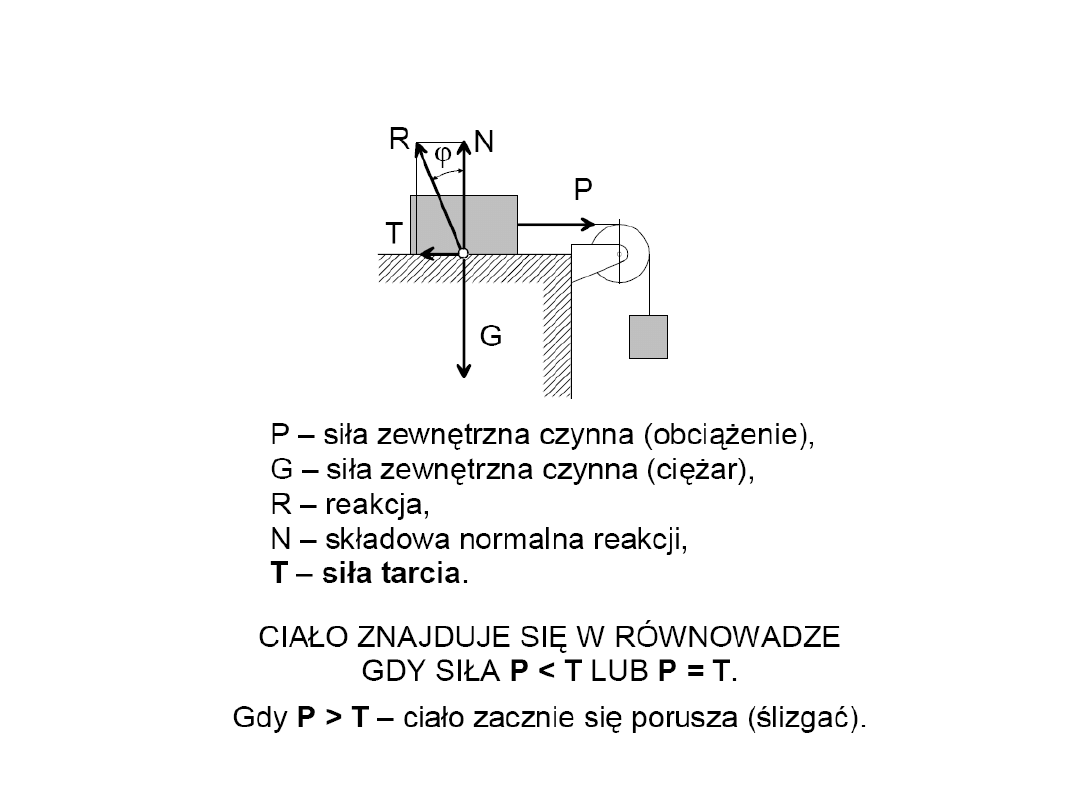
Tarcie i prawa tarcia

39

Prawa tarcia Coulomba

N

T

N

T











1.

Siła tarcia jest niezależna od pola powierzchni
stykających się ze sobą ciał a zależy jedynie od ich
rodzaju, smarowania, wilgotności itp.

2.

Siła tarcia jest skierowana przeciwnie do kierunku
możliwego przesuwu ciała. Jej wartość zmienia się od 0
do T

max

. Wartość T

max

siła tarcia osiąga w chwili utraty

równowagi.

3.

Maksymalna siła tarcia jest proporcjonalna do reakcji
normalnej.

-

dla ciała pozostającego spoczynku

-

dla ciała ślizgającego się

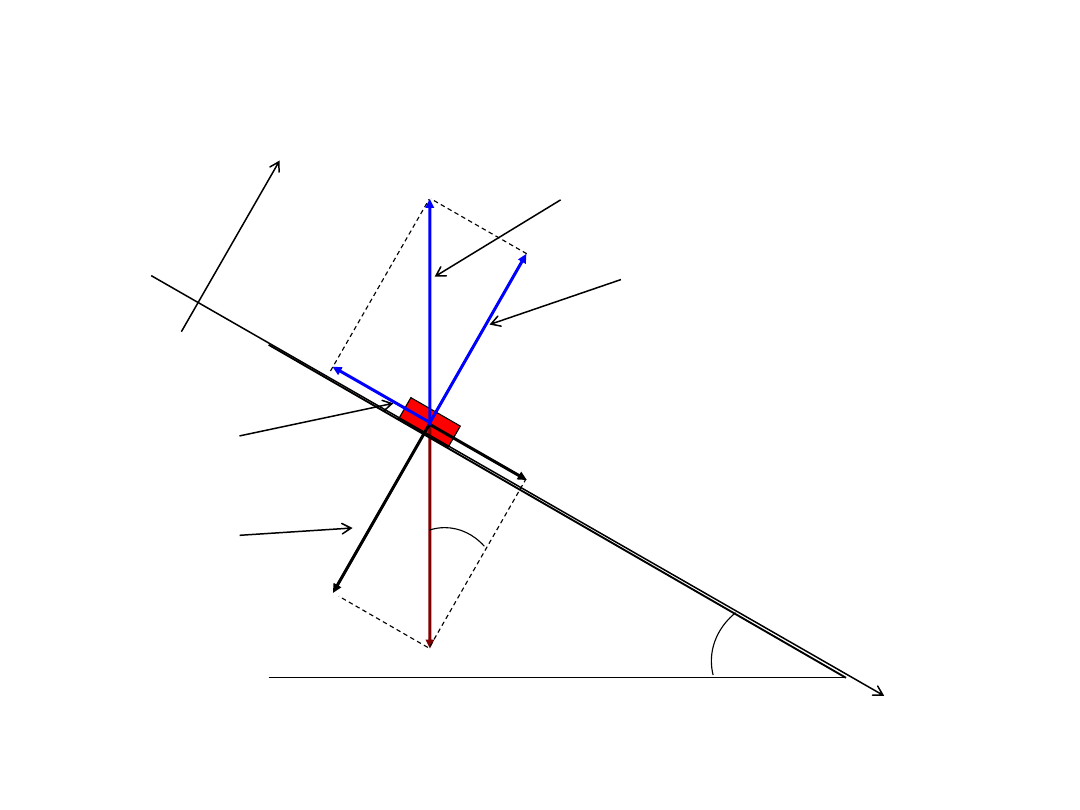
40

y

x

G

N

T

R

y

R

m

0

reakcja normalna równi

siła tarcia

wypadkowa siła reakcji



sin

G

P

x





cos

G

N



P

x



mg

G



siła nacisku



N

T





max

Siła tarcia na równi pochyłej

Przypadek graniczny: P

x

= T

max

41

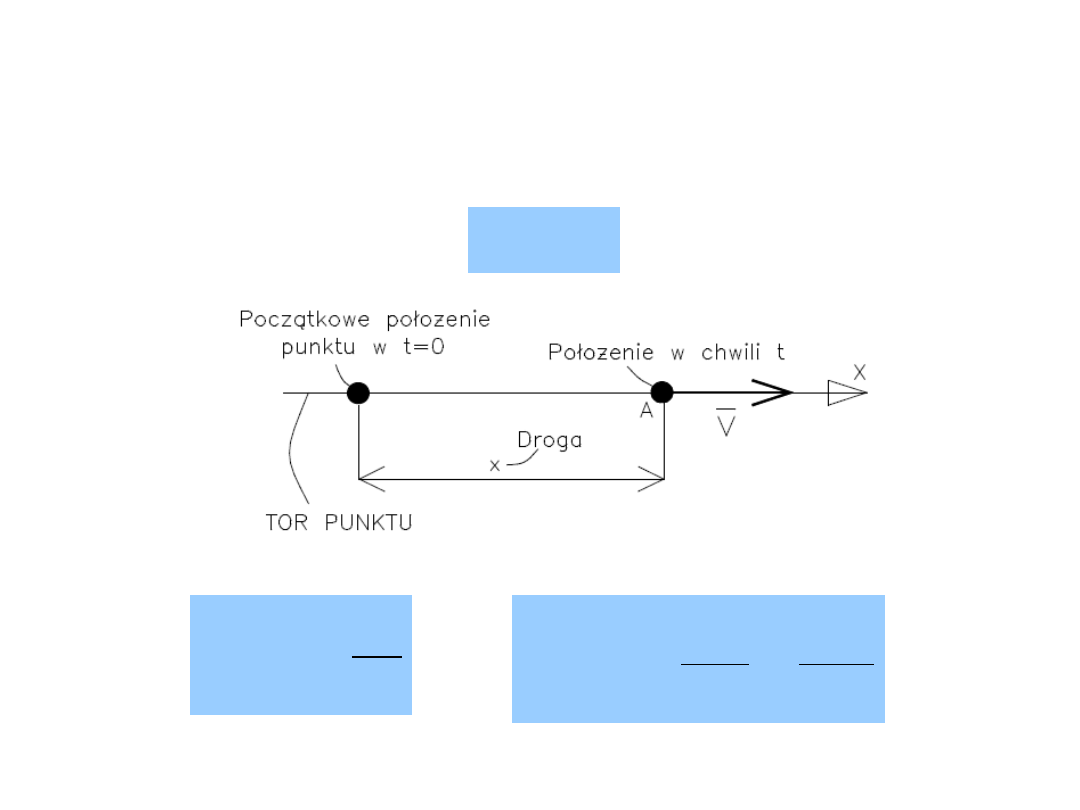
Kinematyka

-

dział mechaniki zajmujący się ruchem ciał,

bez wnikania w związki między ruchem a siłami, które ten
ruch wywołały.

Ruch ciała

-

zjawisko zmiany w czasie położenia tego ciała

względem innego ciała, umownie przyjętego za nieruchome.

Układ odniesienia

-

układ współrzędnych sztywno

związany z ciałem odniesienia.

Czas

jest pojęciem pierwotnym, jest nieodwracalny,

niezależny od wyboru układu odniesienia, taki sam dla
wszystkich punktów układu.

Przestrzeń Euklidesa

-

trzy współrzędne prostokątne plus

czas

Kinematyka

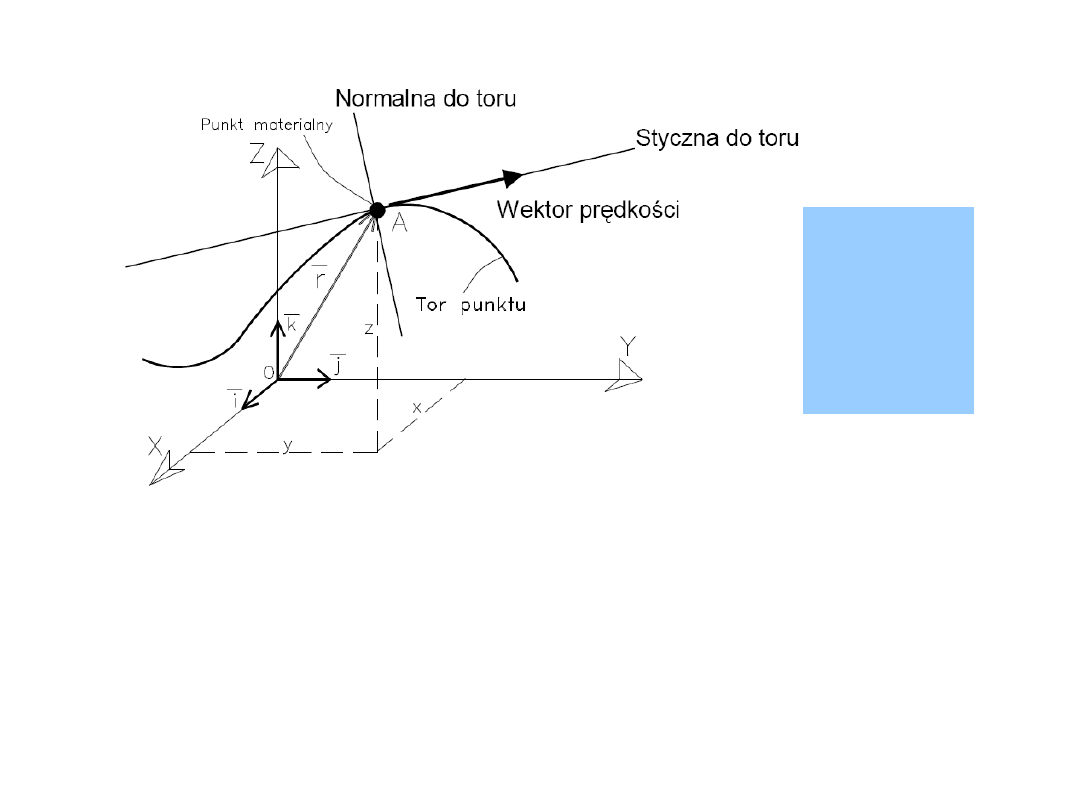
42

Tor ruchu (trajektoria)

-

miejsce geometryczne kolejnych położeń

ruchomego punktu w przestrzeni.

Promień wodzący

-

wektor o początku w początku układu

współrzędnych i końcu w rozpatrywanym punkcie.

Równanie trajektorii ruchu

-

równanie krzywej otrzymanej po

wyrugowaniu czasu z równań ruchu.

Równania ruchu punktu we współrzędnych prostokątnych

 

 

 

t

f

z

t

f

y

t

f

x

z

y

x







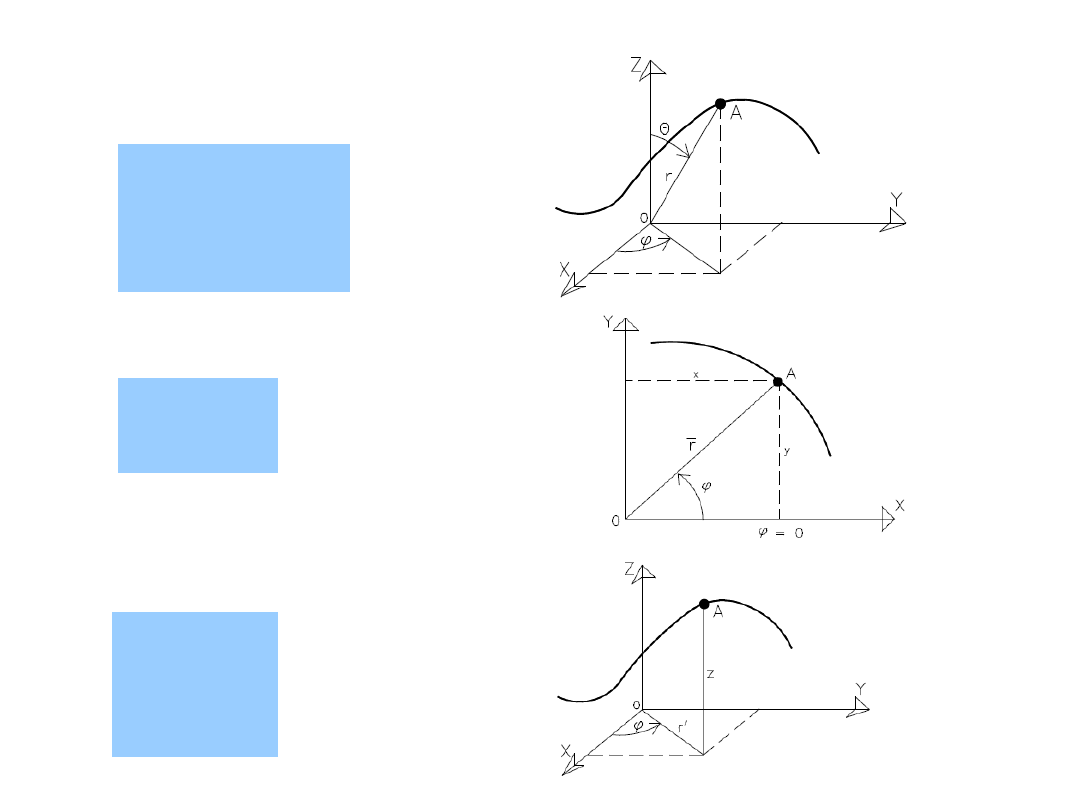
43

Inne układy współrzędnych:

biegunowy w przestrzeni (r,



,



):

walcowy (r,



,z):





sin

cos

r

y

r

x





biegunowy na płaszczyźnie (r,



):











cos

sin

sin

cos

sin

r

z

r

y

r

x







z

z

r

y

r

x















sin

cos

44

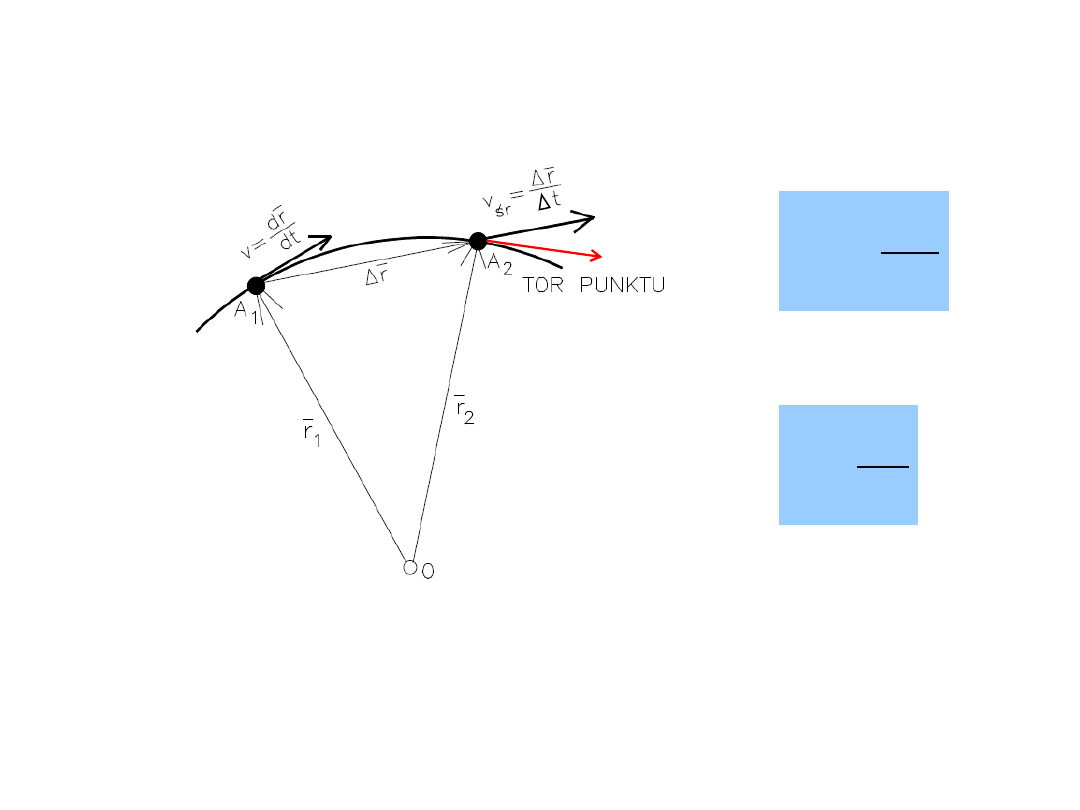
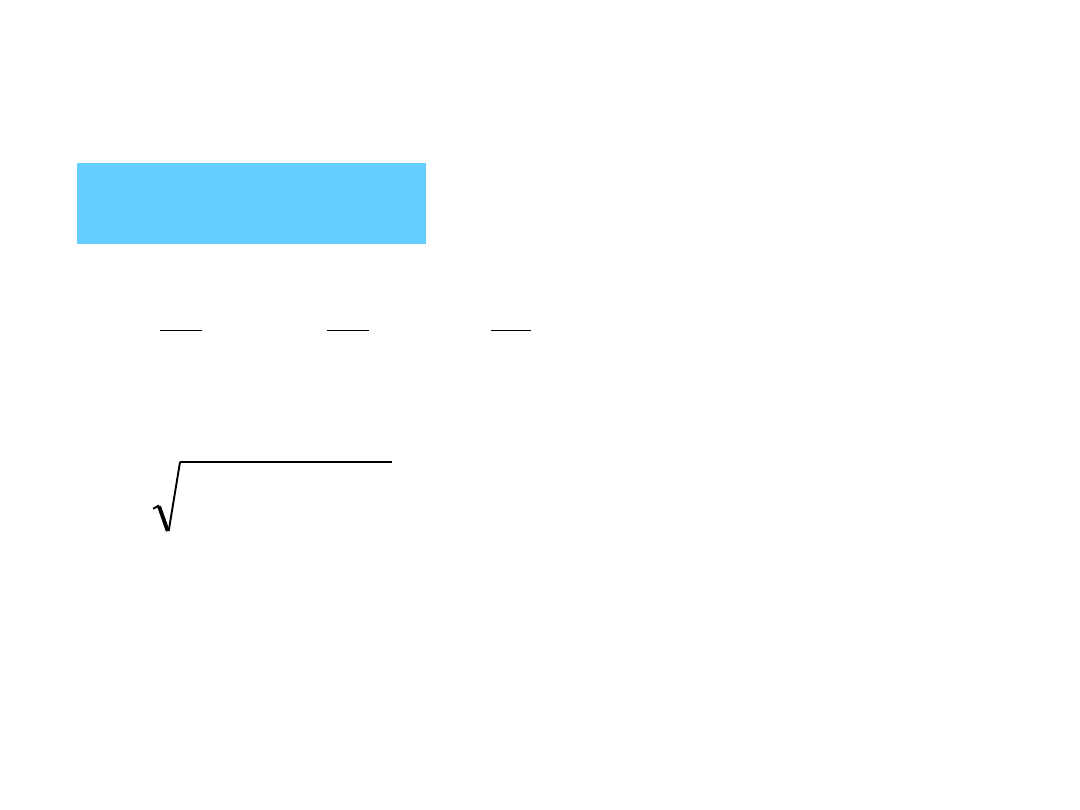
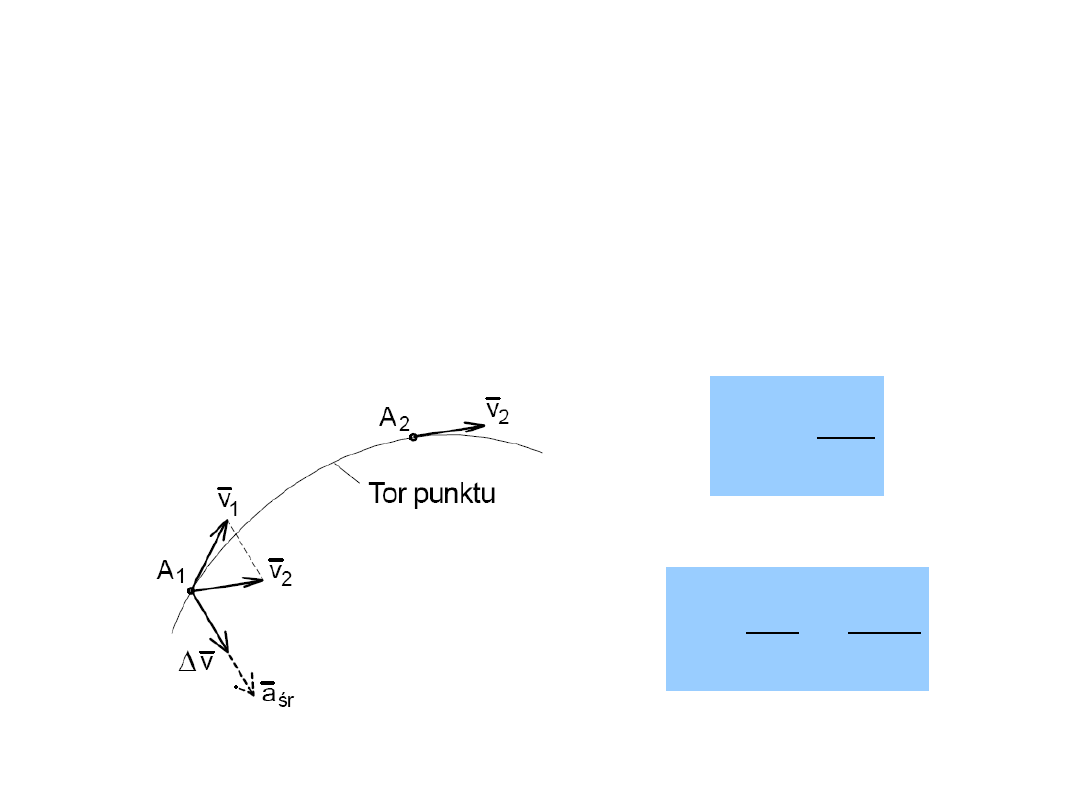
Prędkość punktu w ruchu krzywoliniowym

t

r

v

śr











Prędkość średnia punktu

-

stosunek przyrostu promienia wodzącego

do przyrostu czasu.

Prędkość chwilowa

-

granica, do której dąży stosunek przyrostu

promienia wodzącego do przyrostu czasu, jeśli przyrost czasu dąży do
zera (pierwsza pochodna promienia wodzącego względem czasu).

dt

r

d

v







v

2

45

W układzie współrzędnych prostokątnych:

k

v

j

v

i

v

v

z

y

x















dt

dz

v

dt

dy

v

dt

dx

v

z

y

x







,

,

2

2

2

z

y

x

v

v

v

v







- zapis wektorowy

-

składowe wektora prędkości

-

moduł wektora prędkości

46

Przyśpieszenie punktu

jest wynikiem zmiany kierunku i

wartości prędkości.

Przyśpieszenie punktu w ruchu

krzywoliniowym

2

2

dt

r

d

dt

v

d

a











t

v

a

śr











Przyśpieszenie chwilowe

-

pierwsza pochodna prędkości

względem czasu.

47

W układzie współrzędnych prostokątnych:

k

a

j

a

i

a

a

z

y

x















.

,

,

gdzie

2

2

2

2

2

2

dt

z

d

dt

dv

a

dt

y

d

dt

dv

a

dt

x

d

dt

dv

a

z

z

y

y

x

x













48

1. Podział ze względu na trajektorię ruchu.

Ruch punktu:

- prostoliniowy,
-

po okręgu (harmoniczny prosty),

- dowolny (krzywoliniowy).

Ruch bryły:

-

postępowy,

- obrotowy,
-

płaski,

- kulisty,
- dowolny.

Szczególne przypadki ruchu

49

2. Podział ze względu wartości prędkości i
przyśpieszenia:

-

przyśpieszony jednostajnie (a = const.),

-

przyśpieszony niejednostajnie (a



lub a



),

- jednostajny (v = const),

-

opóźniony jednostajnie (-a = const.),

-

opóźniony niejednostajnie (-a



lub -a



),

Szczególne przypadki ruchu

50

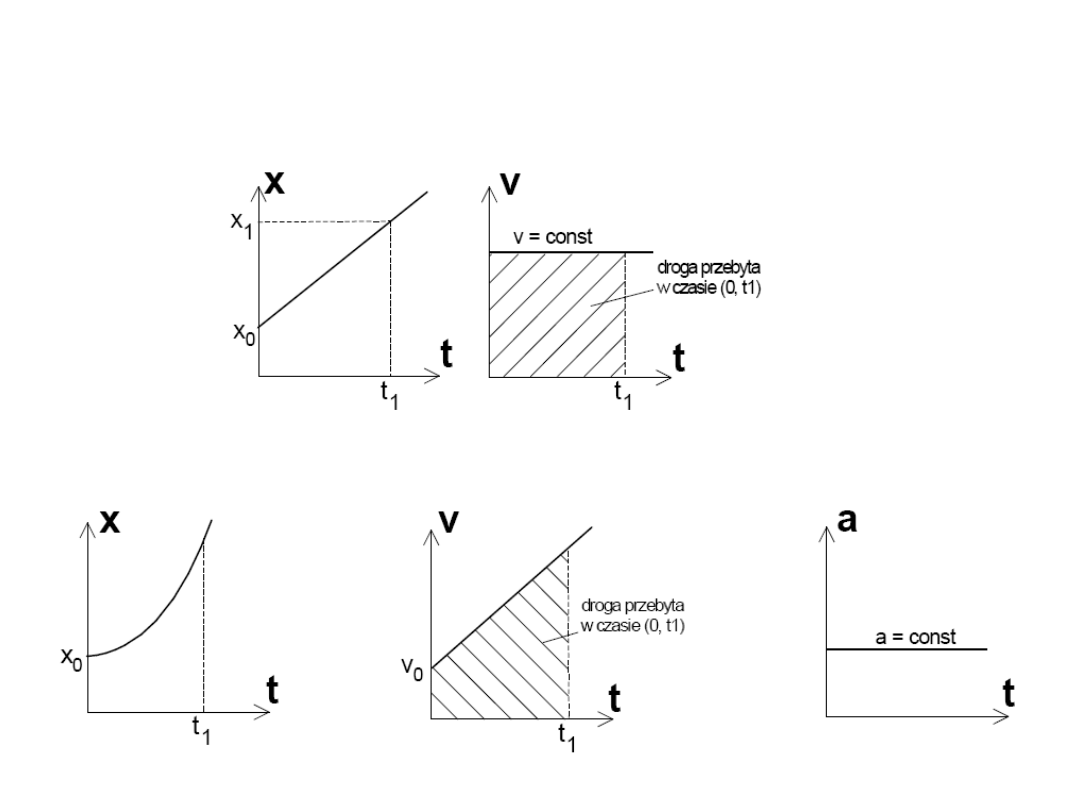
Ruch prostoliniowy

Ruch punktu po linii prostej równoległej do osi OX.

Równanie ruchu:

 

t

x

x



dt

dx

v

v

x





2

2

dt

x

d

dt

dv

a

a

x

x







x

0

51

Ruch prostoliniowy

Ruch jednostajny:

v

= const.

a

= 0

Ruch jednostajnie przyśpieszony:

a

= const.

52

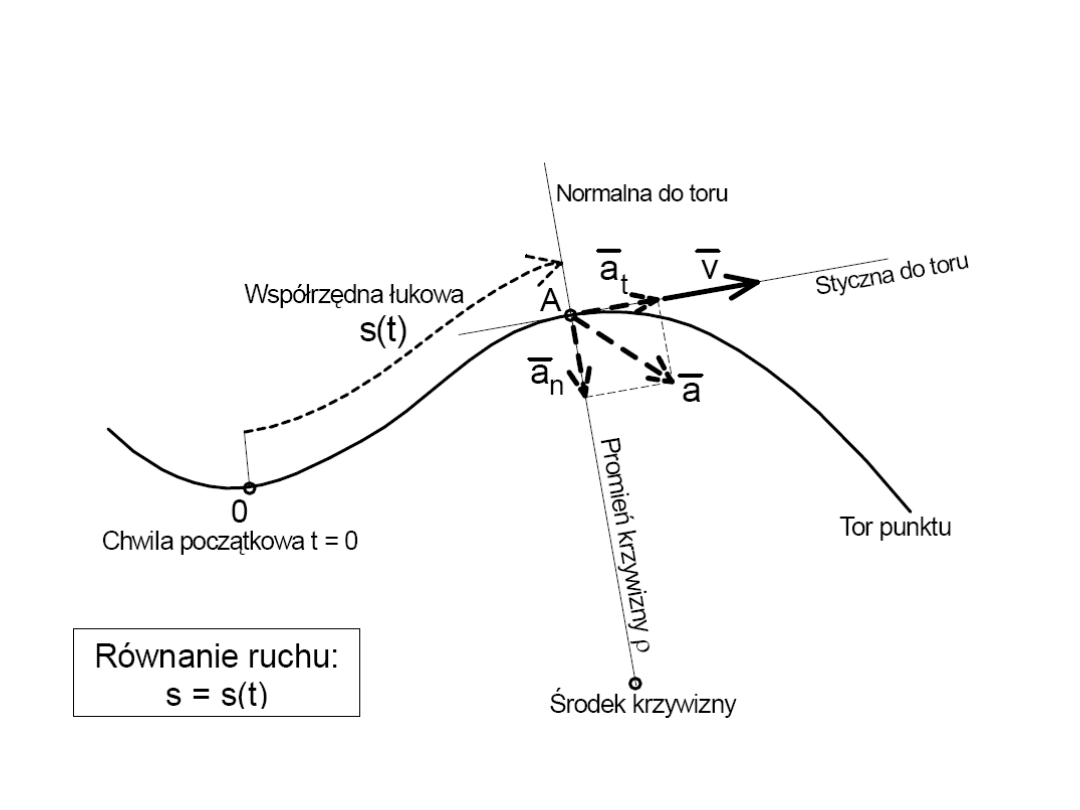
Ruch krzywoliniowy

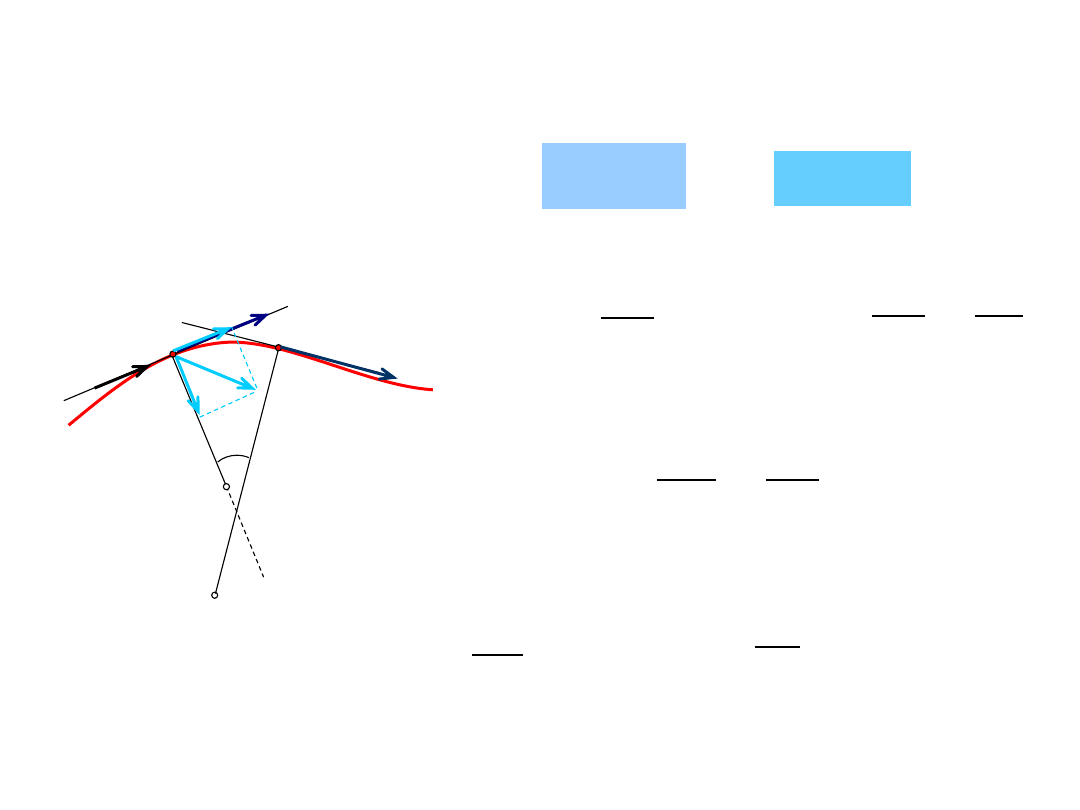
56

Ruch krzywoliniowy

Równanie ruchu:

 

t

s

s





s



v



t

s

v

śr







dt

ds

t

s

v

t













0

lim







v

v



dt

v

d

t

v

a

t



















0

lim

v

1

dt

dv

a

t





2

v

a

n



a

n

a

t

a

57

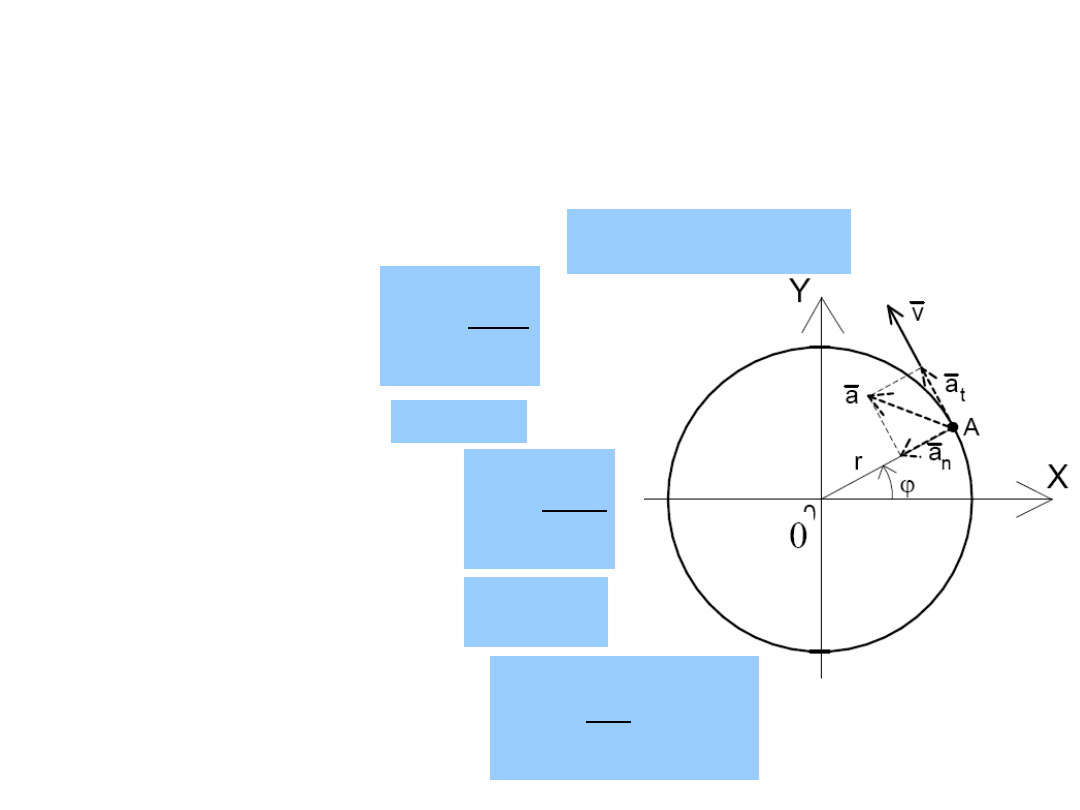
Ruch punktu po okręgu

Ruch punktu po okręgu jest przypadkiem szczególnym
ruchu krzywoliniowego, w którym



= r = const.

Równanie ruchu po okręgu:

 

 

t

r

t

s

s







Prędkość kątowa:

Prędkość liniowa:

dt

d









r

v



Przyśpieszenie kątowe:

dt

d







Przyśpieszenie styczne:



r

a

t



Przyśpieszenie normalne:

r

r

v

a

n

2

2







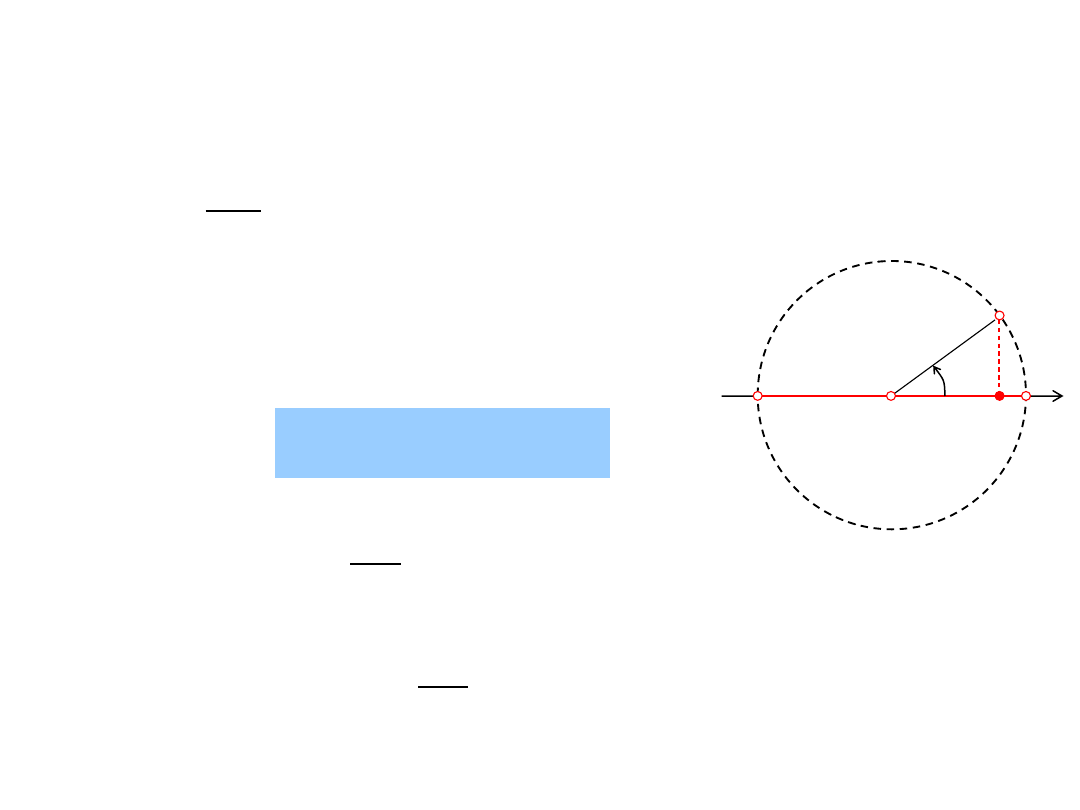
58

Ruch harmoniczny

Równanie ruchu harmonicznego prostego:





0

cos









t

r

x

Prędkość:





x

t

r

dt

dv

a

2

0

2

cos

























0

sin















t

r

dt

dx

v

Przyśpieszenie:



cos

r

x



0

t

const





















dt

d

r

A

A’

0

x



x

59

Ruch drgający

-

ruch, w którym występuje okresowa

zmiana współrzędnej.

Okres drgań

-

przedział czasu T, w którym punkt,

wychodząc z pewnego położenia ekstremalnego, wraca
ponownie do niego.

Amplituda drgań

-

największa odległość punktu od środka

drgań.

Faza drgań

-

wartość argumentu funkcji okresowej.

W ruchu harmonicznym:

0











t

T





2



- pulsacja

0



-

faza początkowa

61

Ruch złożony punktu materialnego

Ruch

złożony – wtedy, gdy porusza się układ odniesienia.

Ruch

względny – ruch punktu względem układu

ruchomego (prędkość względna v

w

).

Ruch

bezwzględny – ruch punktu względem nieruchomego

układu odniesienia (prędkość bezwzględna v).

w

u

v

v

v











-

prędkość unoszenia

u

v



r

v

v

u



















0

0

v



-

prędkość ruchu postępowego układu odniesienia





-

prędkość kątowa ruchu obrotowego układu odniesienia

r





-

promień wodzący punktu w ruchomym układzie

odniesienia

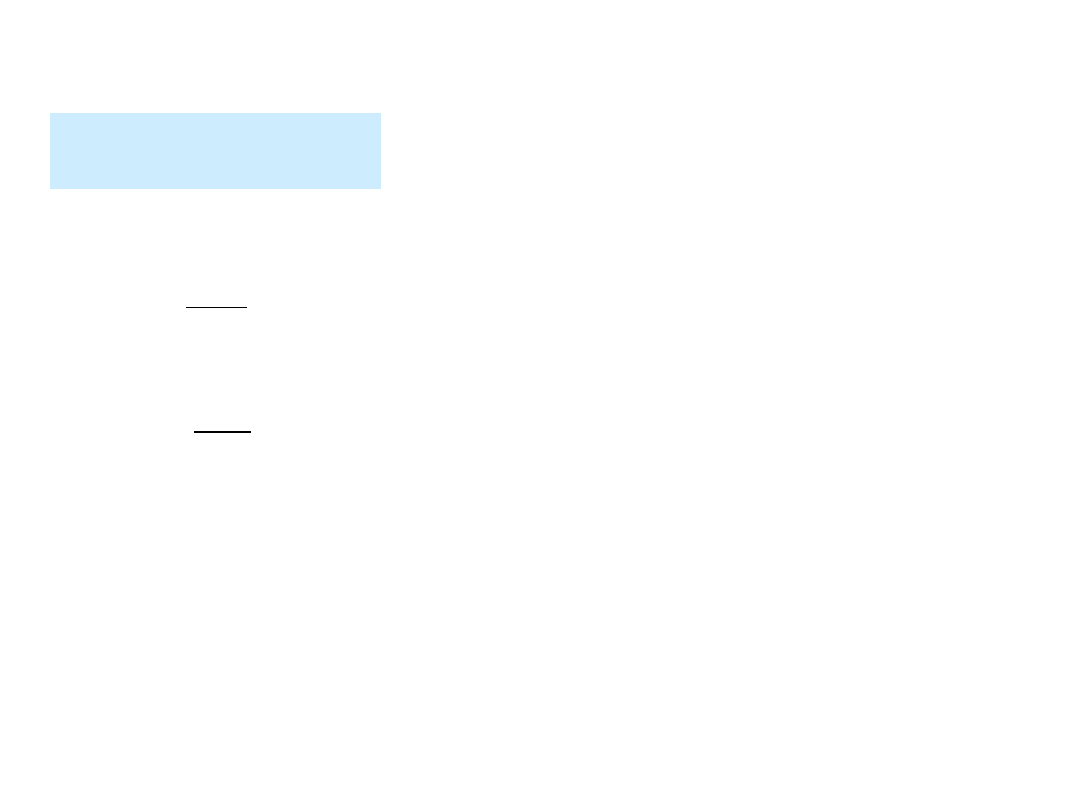
62

Przyśpieszenie w ruchu złożonym

-

przyśpieszenie bezwzględne

C

w

u

a

a

a

a















un

ut

u

a

a

a

a















0

w

a



-

przyśpieszenie ruchu postępowego układu

odniesienia

w

C

v

a













2

-

przyśpieszenie Coriolisa

-

przyśpieszenie unoszenia

dt

v

d

a

0

0







r

dt

d

a

ut















-

przyśpieszenie styczne związane z ruchem

obrotowym układu odniesienia





r

a

un





















-

przyśpieszenie normalne związane z

ruchem obrotowym układu odniesienia

-

przyśpieszenie względem ruchomego układu odniesienia

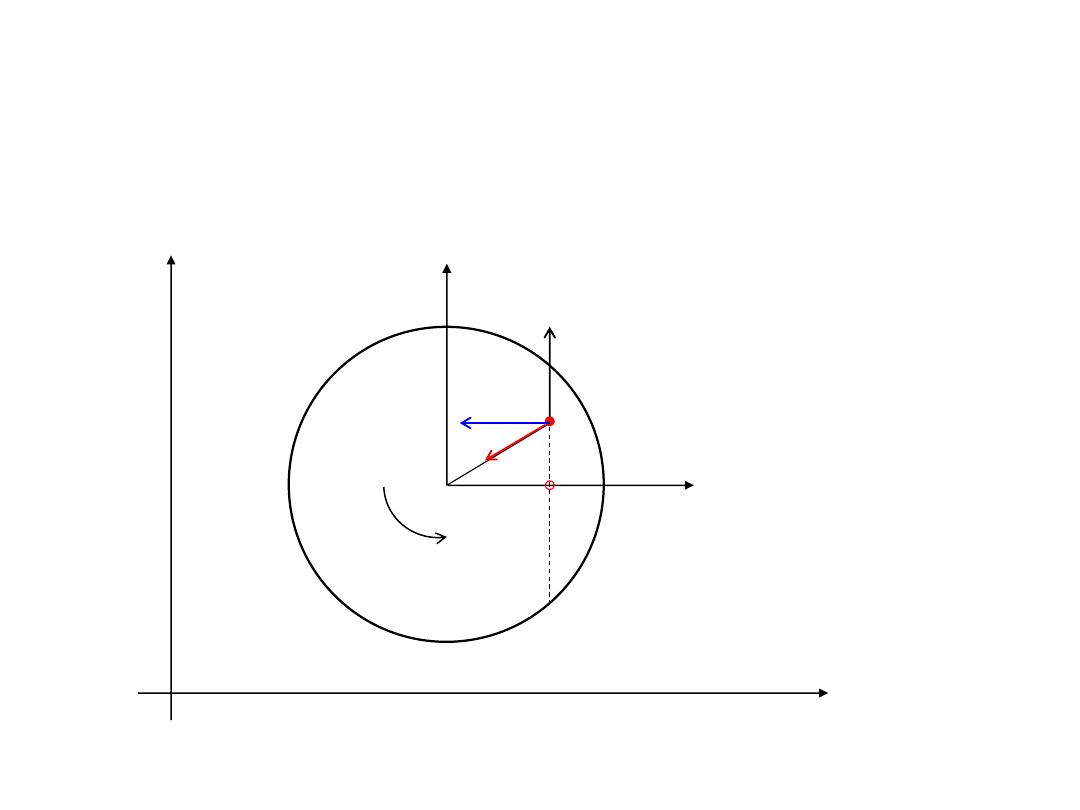
63



y’

y’

x’

r

a

w

a

C

a

un

Przykład: Punkt materialny porusza się z przyśpieszeniem
a

w

= const.

po cięciwie koła wirującego z prędkością

kątową



= const

. W chwili t = 0 ma prędkość względną

v

w

= 0 i zajmuje położenie A

0

. Wyznaczyć przyśpieszenie

punktu.

A

0

y

x

d

r

a

un

2





0

0



a

w

C

v

a



2



C

w

un

a

a

a

a















0



ut

a

64

Ciało sztywne w przestrzeni ma 6 stopni swobody.

Rodzaje ruchu ciała sztywnego:

-

postępowy,

- obrotowy,
-

płaski,

- kulisty,
-

śrubowy,

- dowolny.

Kinematyka ciała sztywnego

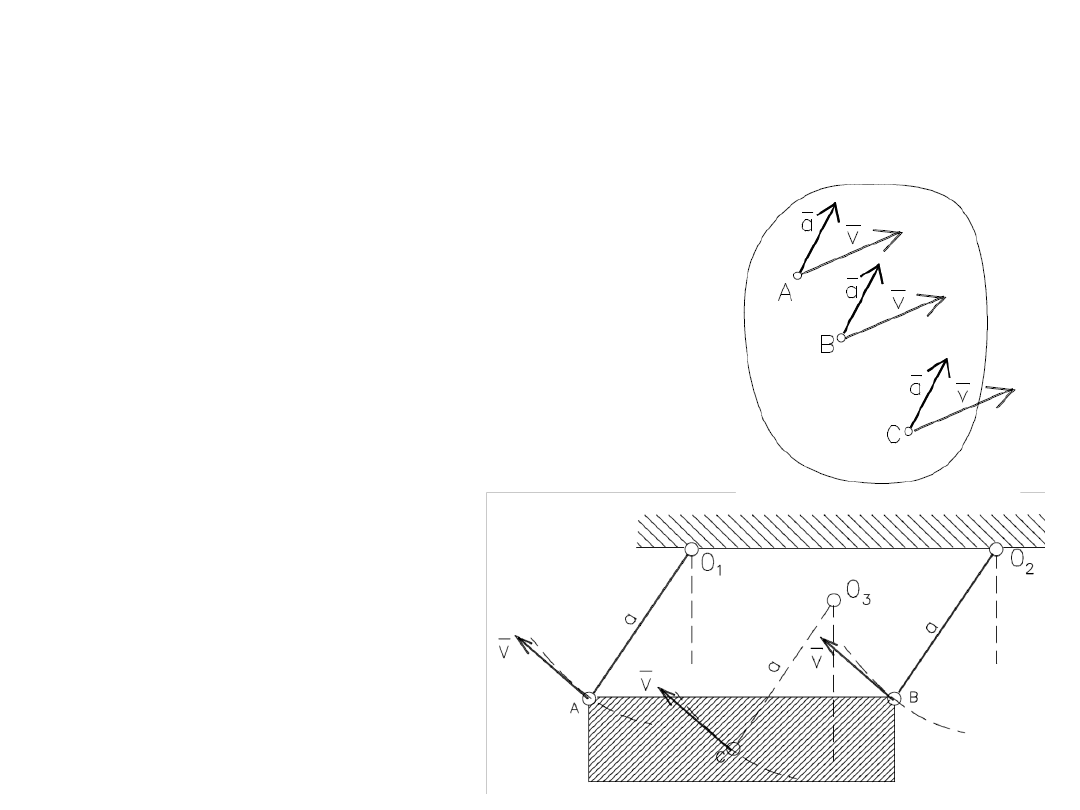
65

W ruchu postępowym wszystkie punkty
ciała poruszają się po identycznych
torach, w każdej chwili mają takie same
prędkości i przyspieszenia.

Dla analizy ruchu postępowego ciała
sztywnego wystarczy określenie ruchu
jednego punktu tego ciała.

Ruch postępowy

Przykłady ruchu postępowego:

-

ruch tłoka w cylindrze,

- ruch kabiny windy,
- ruch suwnicy.

66

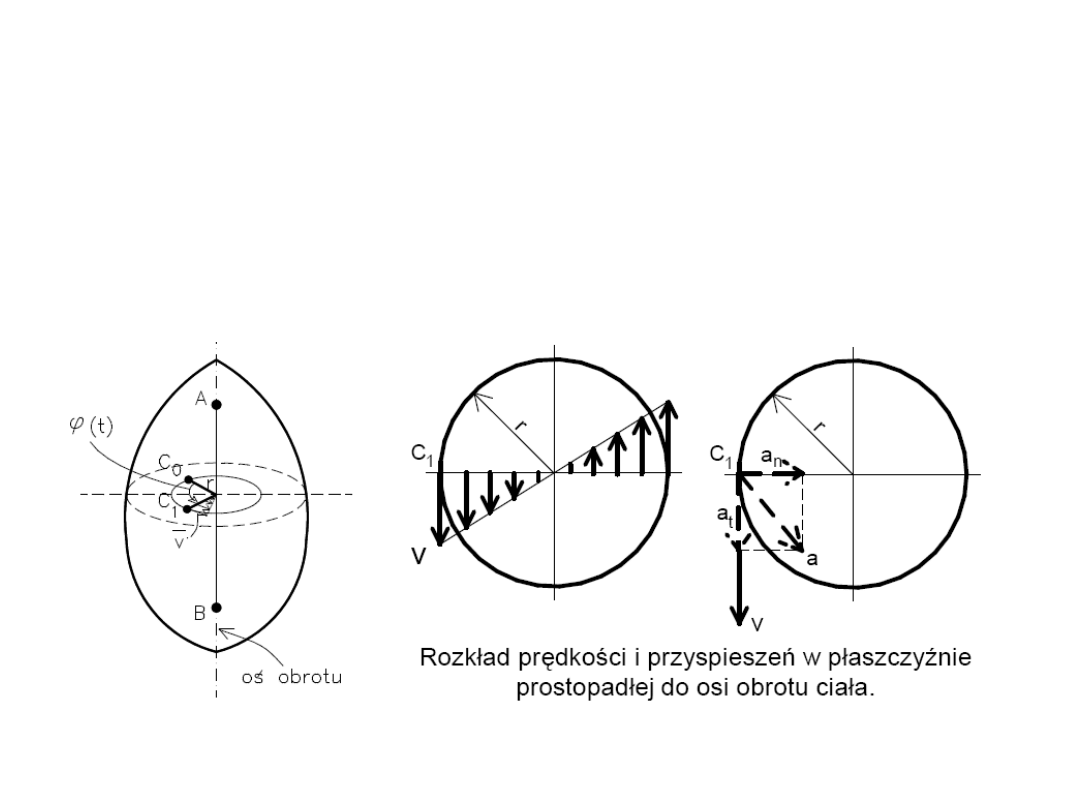
W ruchu obrotowym dwa punkty sztywno związane z ciałem
pozostają nieruchome. Punkty te wyznaczają nieruchomą oś
obrotu

ciała.

Ruch obrotowy

67

Prędkość dowolnego punktu ciała jest równa iloczynowi
prędkości kątowej i odległości od osi obrotu:

Przyśpieszenie styczne:

Przyśpieszenie dośrodkowe:

Przypadki szczególne ruchu obrotowego:

- ruch obrotowy jednostajny,
- ruch obrotowy jednostajnie przyspieszony.



r

v







r

dt

d

r

dt

dv

a

t







2

2

2

2





r

r

r

r

v

a

n







68

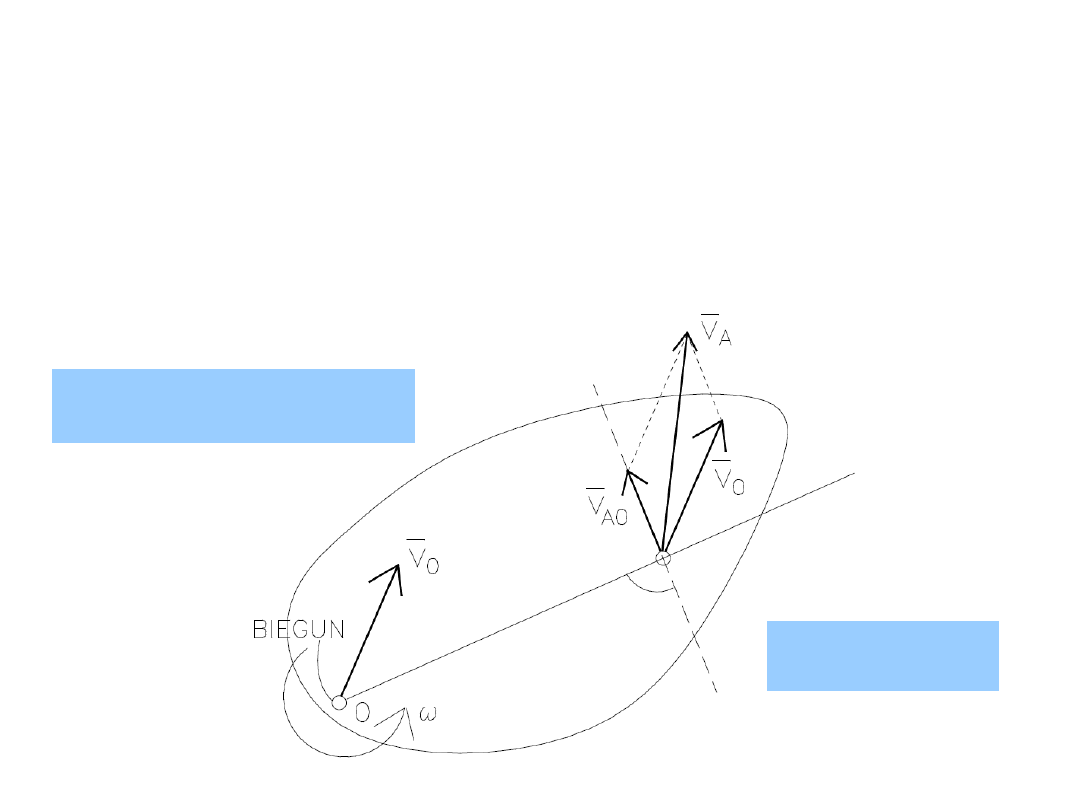
W ruchu płaskim wszystkie punkty ciała poruszają się w
płaszczyznach równoległych do pewnej nieruchomej
płaszczyzny, zwanej płaszczyzną kierującą.

Ruch płaski jest złożeniem chwilowego ruchu postępowego
oraz chwilowego ruchu obrotowego.

Ruch płaski

0

0

A

A

v

v

v











n

A

t

A

A

a

a

a

a

0

0

0















69

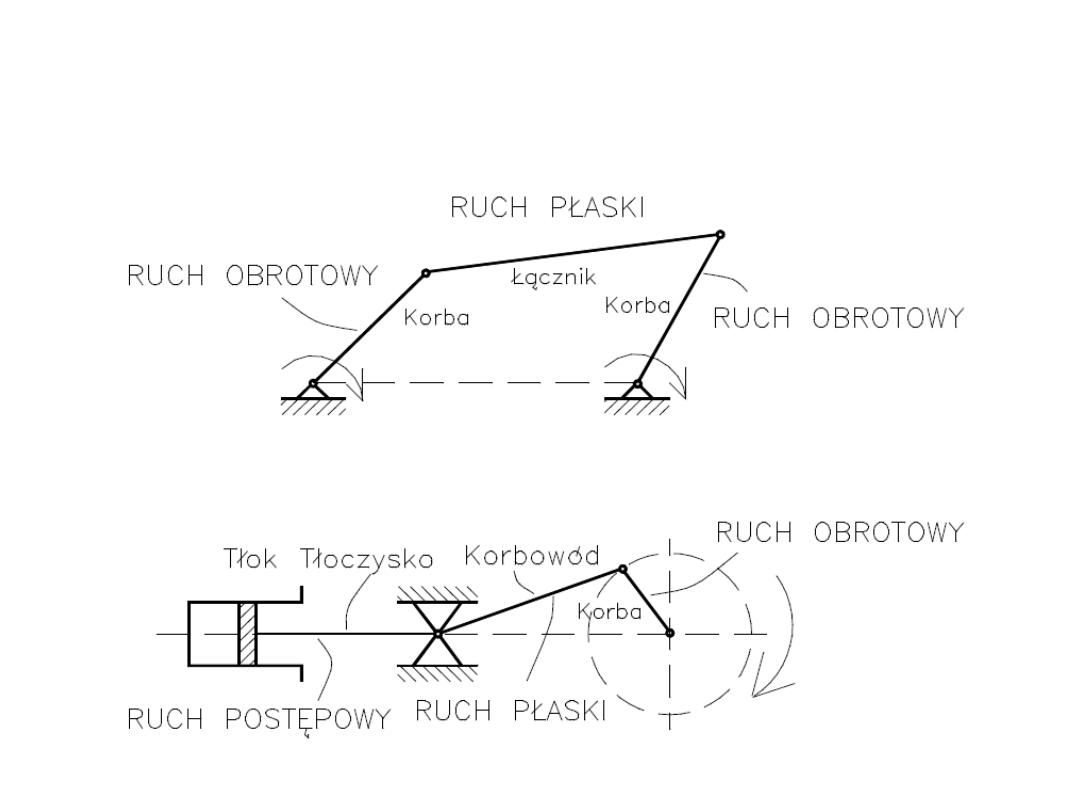
Przykłady ruchu płaskiego

70

W ruchu kulistym jeden punkt ciała jest unieruchomiony.
Ruch ten można traktować jako ruch obrotowy wokół
chwilowej osi przechodzącej przez ten unieruchomiony
punkt.

Ruch kulisty

Ruch ogólny ciała sztywnego

Ruch ogólny ciała sztywnego można traktować jako ruch
złożony z ruchu postępowego dowolnie wybranego punktu
(bieguna) i ruchu obrotowego wokół chwilowej osi
przechodzącej przez ten punkt.

71

Dynamika

-

dział mechaniki zajmujący się badaniem ruchu

ciał materialnych oraz w związków pomiędzy ruchem a
siłami, które ten ruch wywołały.

Podstawowe pojęcie dynamiki – siła.

Siła

-

wynik wzajemnego, mechanicznego oddziaływania na

siebie co najmniej dwóch ciał. Skutkiem tego oddziaływania
jest wyprowadzenie ciała ze stanu spoczynku lub zmiana
parametrów ruchu ciała już poruszającego się.

Podstawą dynamiki są trzy prawa Newtona (1643-1727)
zwane zasadami dynamiki.

Dynamika

73

Przyśpieszenie punktu materialnego jest wprost
proporcjonalne do siły działającej na ten punkt i ma kierunek
tej siły.

Druga zasada dynamiki Newtona

(prawo zmienności ruchu)

P

a

m







Równanie dynamiki ruchu punktu materialnego:

P



-

wypadkowa siła działająca na punkt materialny,

a



-

przyśpieszenie wywołane siłą P,

m

-

masa (miara bezwładności punktu materialnego).

76

Zagadnienie proste dynamiki

-

znane jest równanie ruchu

x = x(t) a szukany jest przebieg czasowy siły P(t).

Zagadnienie odwrotne dynamiki

– dana jest siła P, która

może być funkcją czasu, położenia i prędkości:

a szukane jest równanie ruchu x = x(t).

Równanie dynamiki ruchu prostoliniowego

punktu materialnego

x

P

dt

x

d

m



2

2





x

x

t

P

P







,

,



77

Siła ciężkości:

Równanie dynamiki ruchu:

Ruch punktu materialnego pod wpływem

siły ciężkości (spadek pionowy)

g

dt

x

d



2

2

const





g

m

G





2

,

2

0

0

0

gt

t

v

x

x

gt

v

v

x











ruch jednostajnie
przyśpieszony

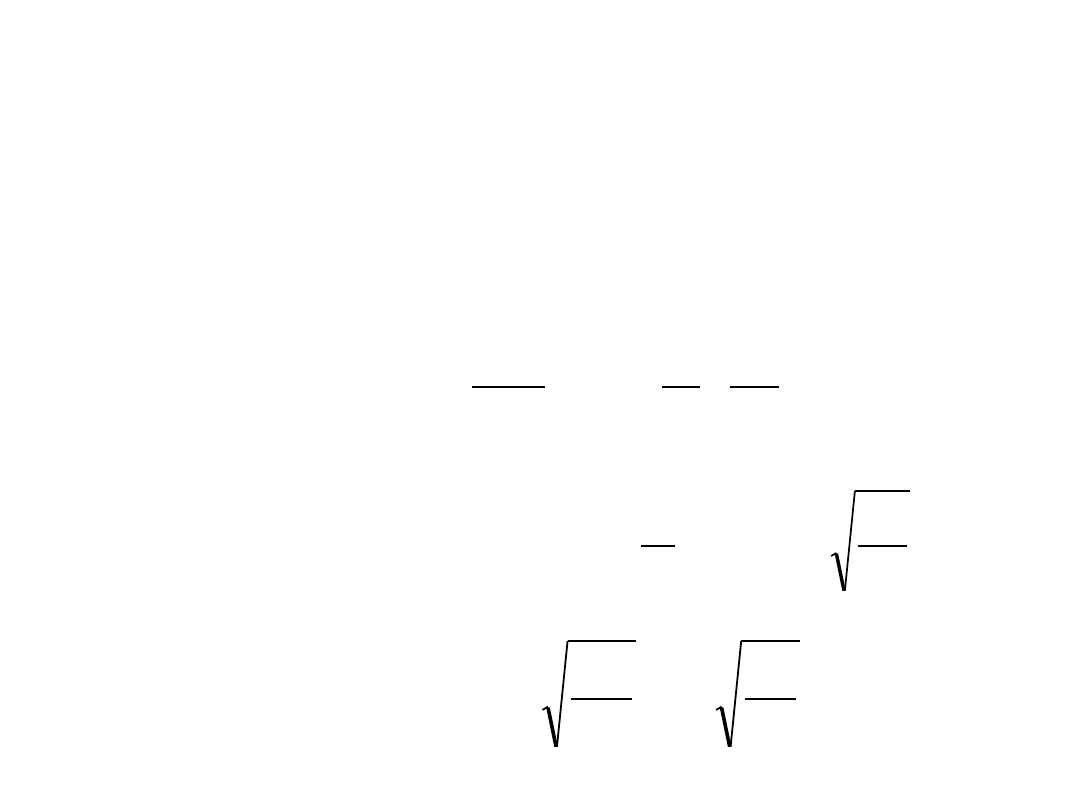
78

Siła oporu aerodynamicznego w powietrzu:

Wypadkowa siła:

Równanie dynamiki:

Spadek pionowy w ośrodku stawiającym opór

2

x

kv

R



 

































t

m

gk

k

m

t

x

cosh

ln

2

x

x

kv

mg

R

G

P









2

2

2

















dt

dx

m

k

g

dt

x

d

Gdy x

0

=0 i v

0

=0, to

równanie ruchu ma postać:

 

















t

m

gk

k

mg

t

v

x

tgh

Przebieg czasowy
prędkości:

79

Punkt swobodny porusza się zawsze w kierunku działania
wypadkowej siły P.

Jeśli na punkt materialny działają więzy, kierunek ruchu nie
pokrywa się z kierunkiem działania siły.

Występuje wtedy siła reakcji więzów R.

Ruch prostoliniowy nieswobodnego

punktu materialnego

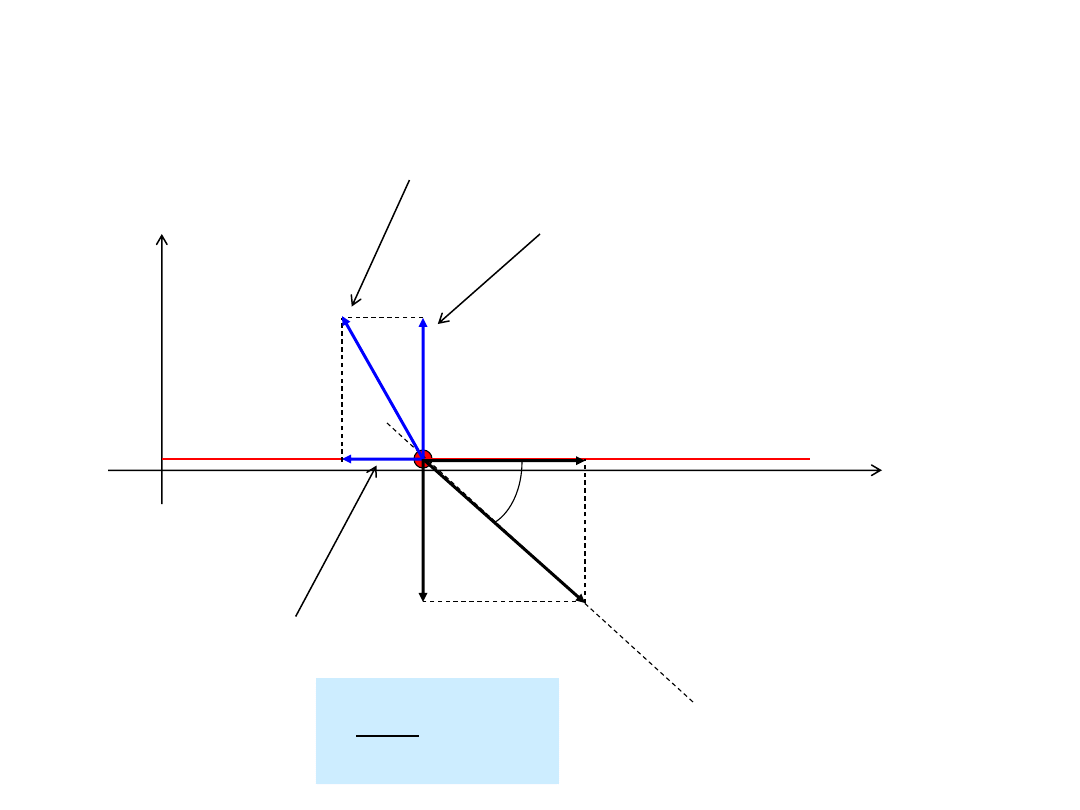
80

y

x

P

m

tor ruchu = kierunek ruchu

kierunek działania siły

0

T

siła tarcia

R

y

siła reakcji toru w osi y

R

wypadkowa siła reakcji więzów

T

P

dt

x

d

m

x





2

2

Przykład 1: Siła czynna P działa na punkt materialny pod kątem



względem toru, po którym porusza się punkt, w obecności siły tarcia T.

P

x

P

y



cos

P

P

x





sin

P

P

y





y

y

P

R



81

y

x

G

m

0

T

G

dt

x

d

m

x





2

2

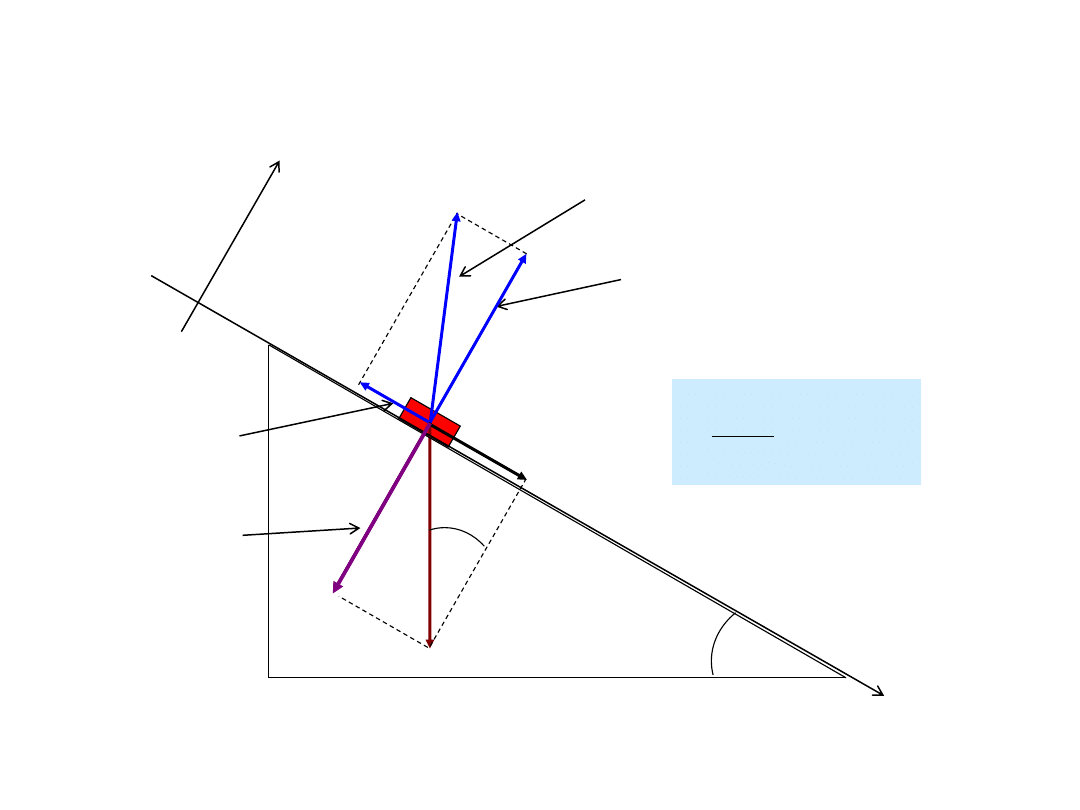
Przykład 2: Ciało o masie m porusza się pod wpływem siły ciężkości

po równi pochyłej o kącie



i współczynniku tarcia



.

R

wypadkowa siła reakcji

T

siła tarcia



mg

G



R

y

reakcja normalna równi



sin

G

G

x





cos

G

G

y



G

y

G

x









cos

mg

N

T





y

y

G

R



y

R

N



siła nacisku

N

82

y

x

P

G

T

m

0

T

P

ma

x

x





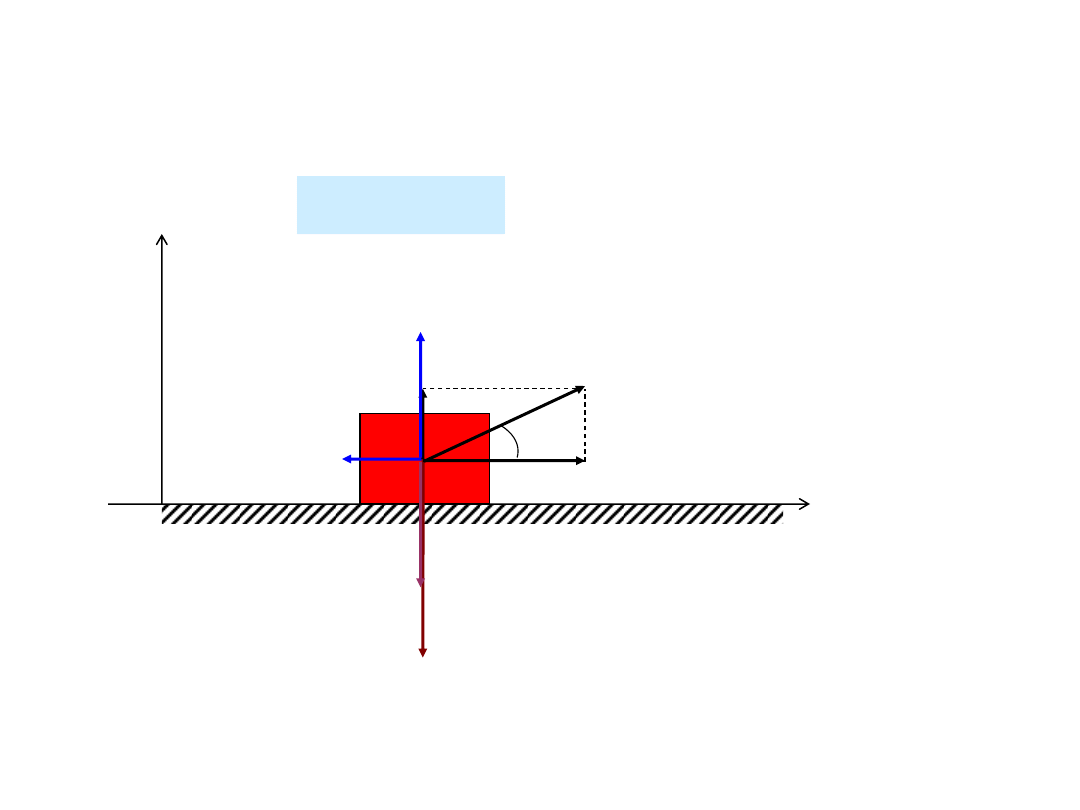
Przykład 3: Znaleźć przyśpieszenie ciała o masie m, do którego

przyłożono siłę P pod kątem



względem płaszczyzny ruchu.

y

R

N



N

P

x



cos

P

P

x





sin

P

P

y



P

y



R

y

G

R

P

y

y









y

P

G

N

T











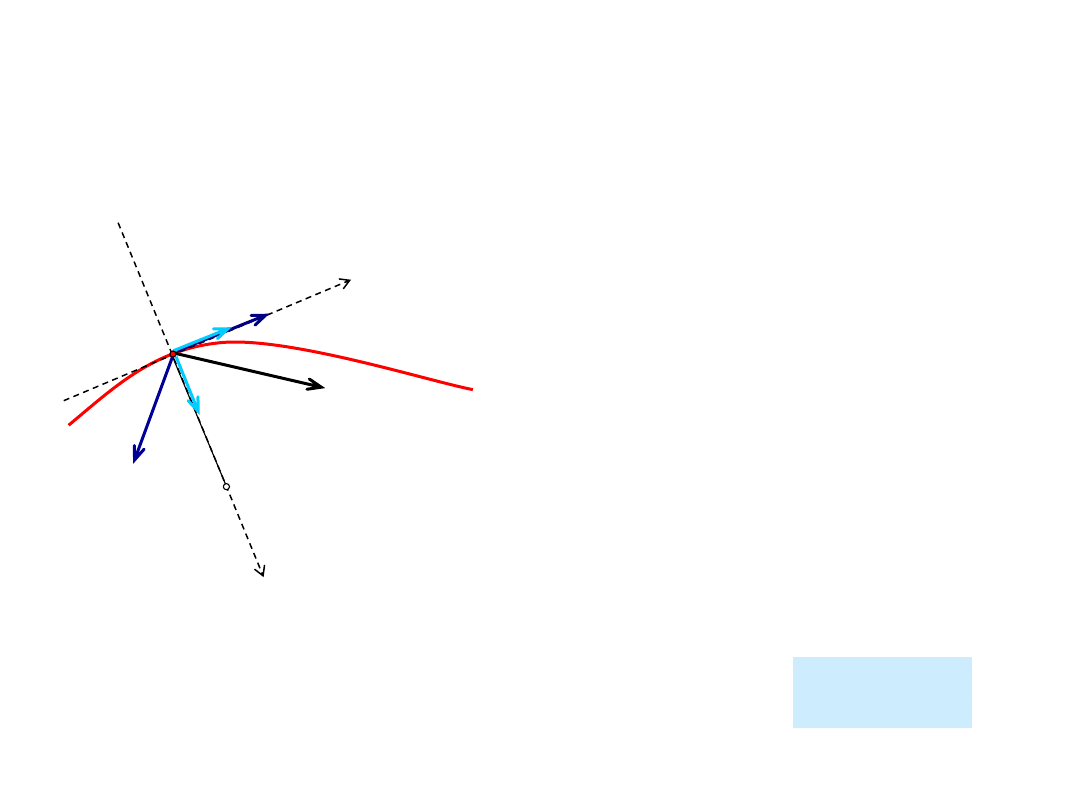
83

Ruch krzywoliniowy nieswobodnego

punktu materialnego

R

v



a

n

a

t

P

n

Jeśli więzy nałożone na punkt
materialny są idealne, siła reakcji
więzów działa wzdłuż normalnej
do toru.

Jeśli więzy są rzeczywiste, siła
reakcji więzów R ma dwie
składowe: normalną R

n

i styczną R

t

.

N

R

n



n

t

R

N

T

R











n

t

R

R





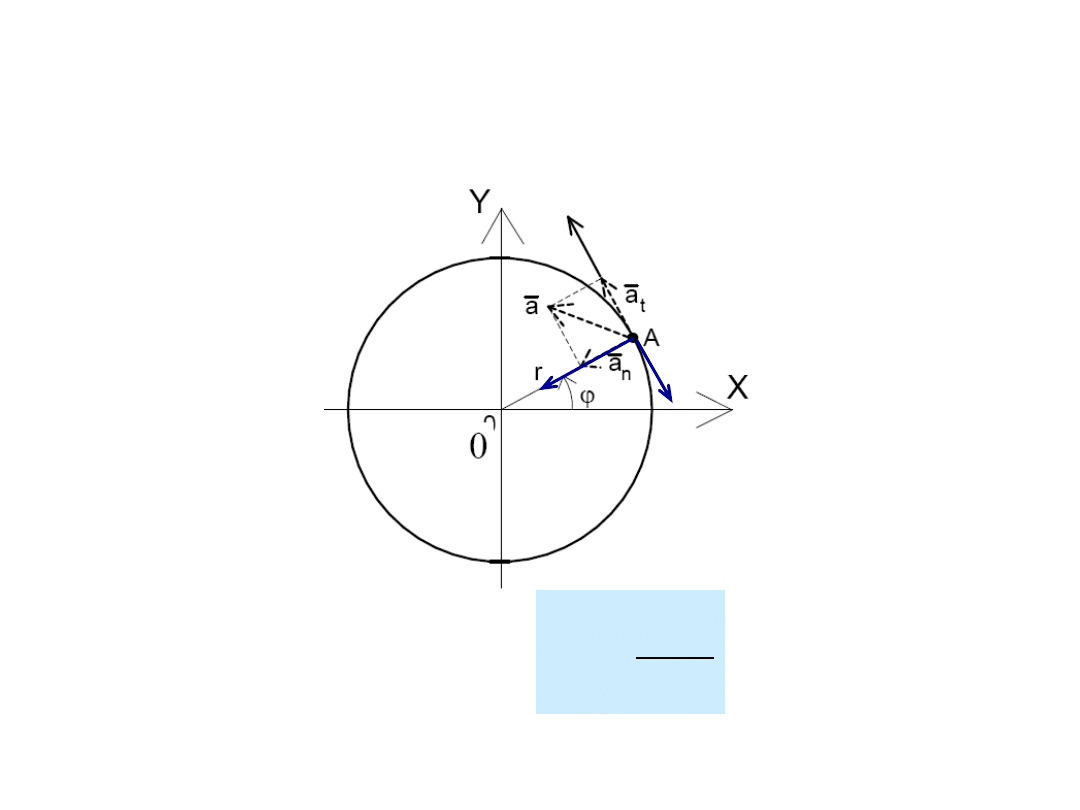
84

R

n

P

t

R

t

Ruch punktu materialnego po okręgu

R

n

– siła dośrodkowa

r

mv

R

n

2



85

Podczas ruchu punktu materialnego, w

każdej chwili

wszystkie siły rzeczywiste działające na punkt oraz siła
bezwładności pozostają w równowadze.

a

m

A









Zasada d’Alemberta umożliwia stosowanie równań
równowagi sił w analizie dynamiki ruchu punktu
materialnego:

Zasada

d’Alemberta

-

siła bezwładności (siła d’Alemberta)

Siła bezwładności jest zawsze skierowana przeciwnie
do przyśpieszenia.

0







R

P

A







86

Ruch punktu materialnego pod wpływem siły P

x

proporcjonalnej do wychylenia od stanu równowagi.

Drgania liniowe

cx

P

x





Równanie dynamiki ruchu:

cx

dt

x

d

m





2

2

Rozwiązanie ogólne:

t

C

t

C

x

0

2

0

1

cos

sin









m

c



0



-

pulsacja drgań własnych

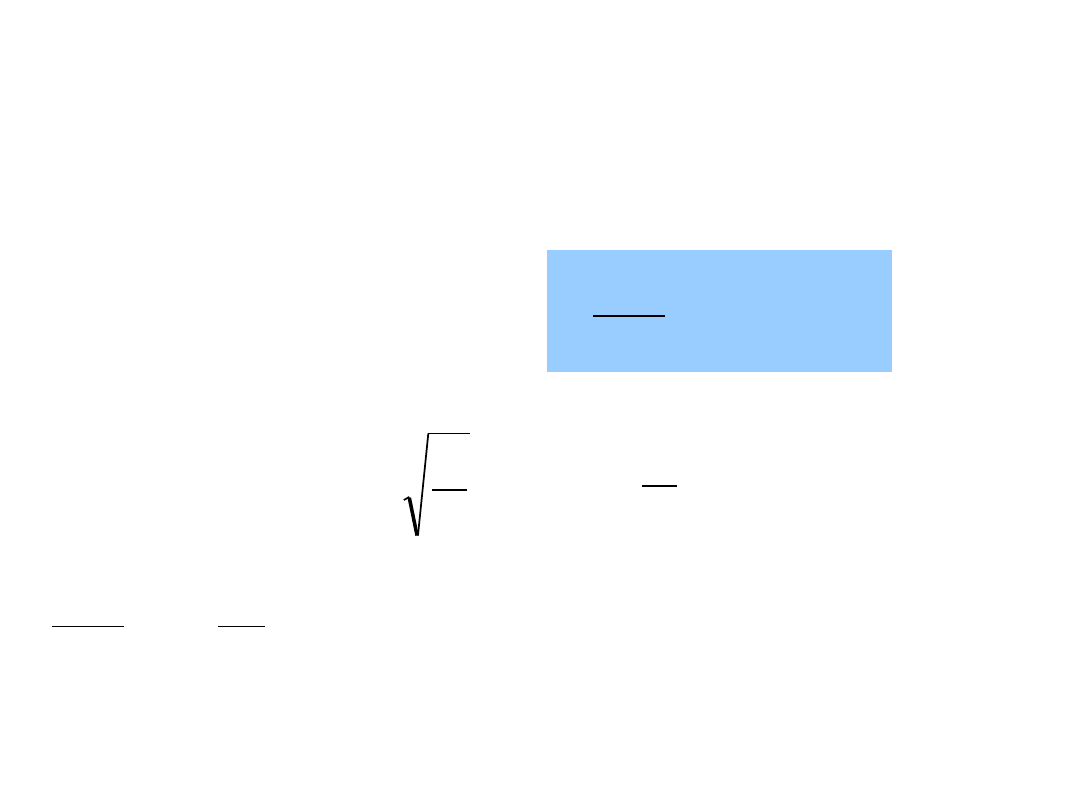
87

Oprócz siły P

x

proporcjonalnej do wychylenia działa siła

oporu ruchu R

x

proporcjonalna do prędkości:

Drgania liniowe z tłumieniem

x

x

R







Równanie dynamiki ruchu:

x

cx

dt

x

d

m









2

2

Podstawiając:

,

0

m

c





otrzymuje się:

m

n





2

0

2

2

0

2

2







x

dt

dx

n

dt

x

d



-

równanie różniczkowe 2-go

rzędu o stałych współczynnikach

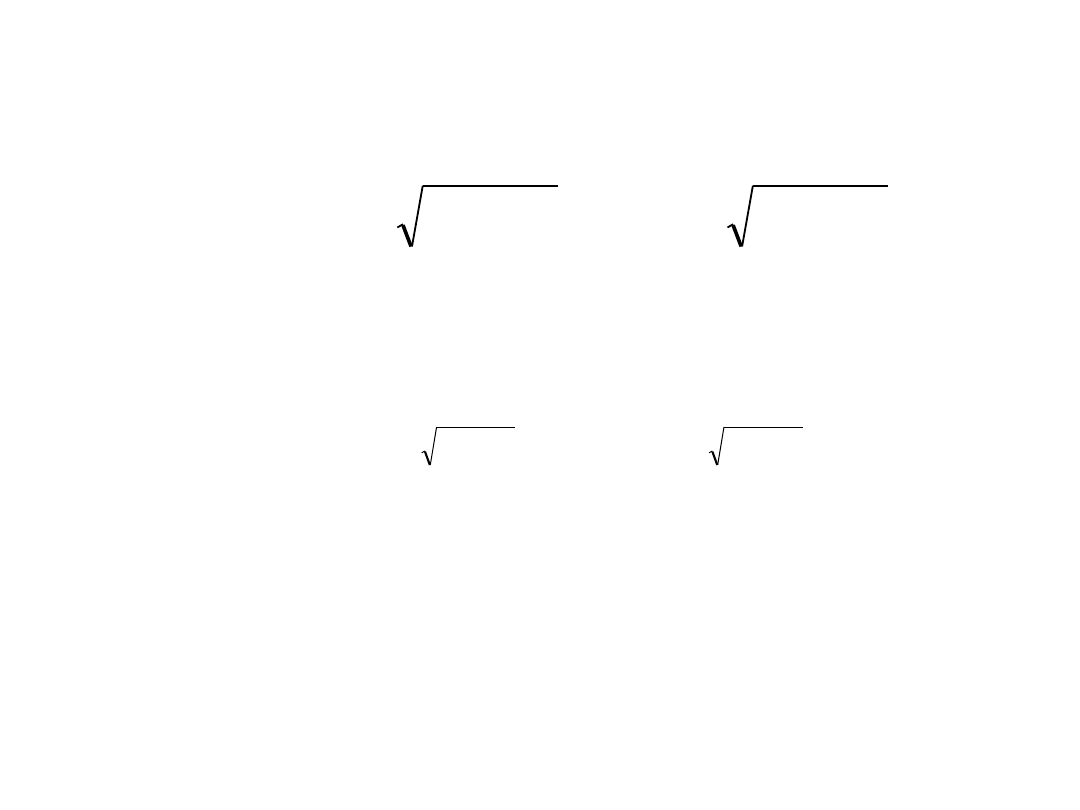
88

Rozwiązanie:
1. Jeżeli n <



0

(tłumienie podkrytyczne) - drgania tłumione:





t

n

C

t

n

C

e

x

nt

2

2

0

2

2

2

0

1

cos

sin















2. Jeżeli n >



0

(tłumienie nadkrytyczne) - przebieg

aperiodyczny:

t

n

n

t

n

n

e

C

e

C

x









































2

0

2

2

0

2

2

1





3

. Jeżeli n =



0

- przebieg aperiodyczny krytyczny:

nt

nt

te

C

e

C

x









2

1

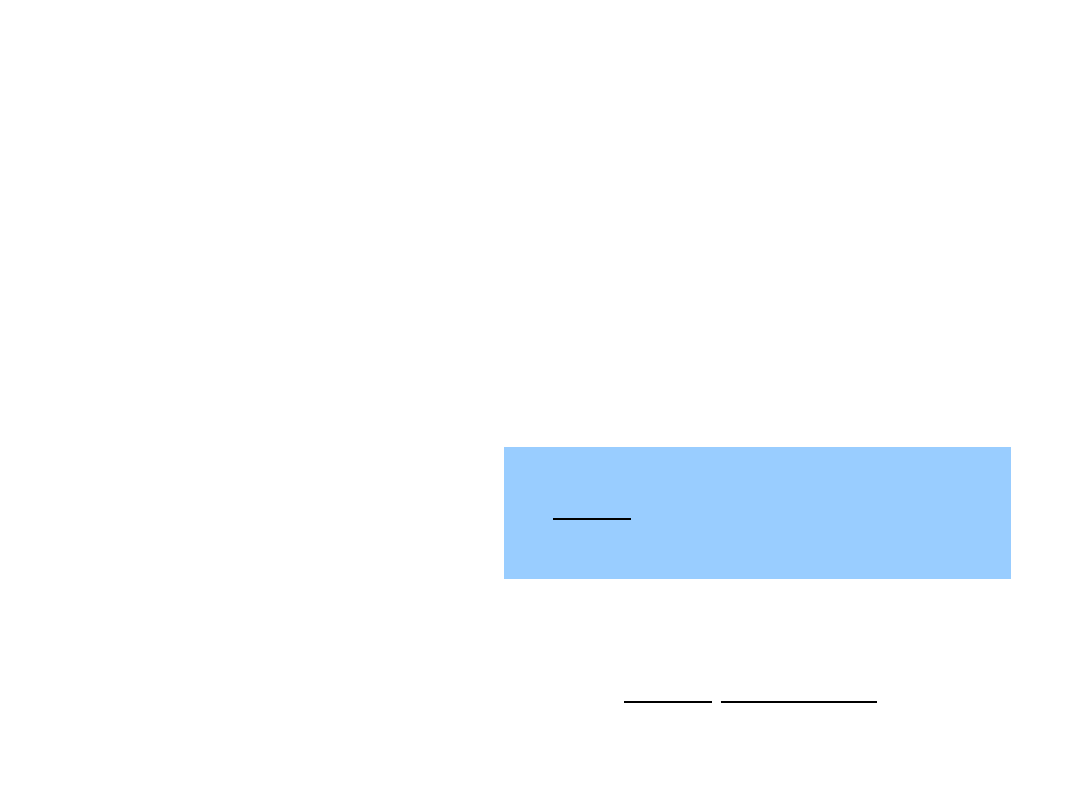
89

Ruch punktu materialnego pod wpływem siły P

x

proporcjonalnej do wychylenia:

Drgania wymuszone nietłumione

cx

P

x





Równanie dynamiki ruchu:

t

F

cx

dt

x

d

m



cos

max

2

2







Rozwiązanie:

t

m

F

t

C

t

C

x











cos

1

cos

sin

2

2

0

max

0

2

0

1









oraz siły F

x

będącej okresową funkcją czasu:

t

F

F

x



cos

max



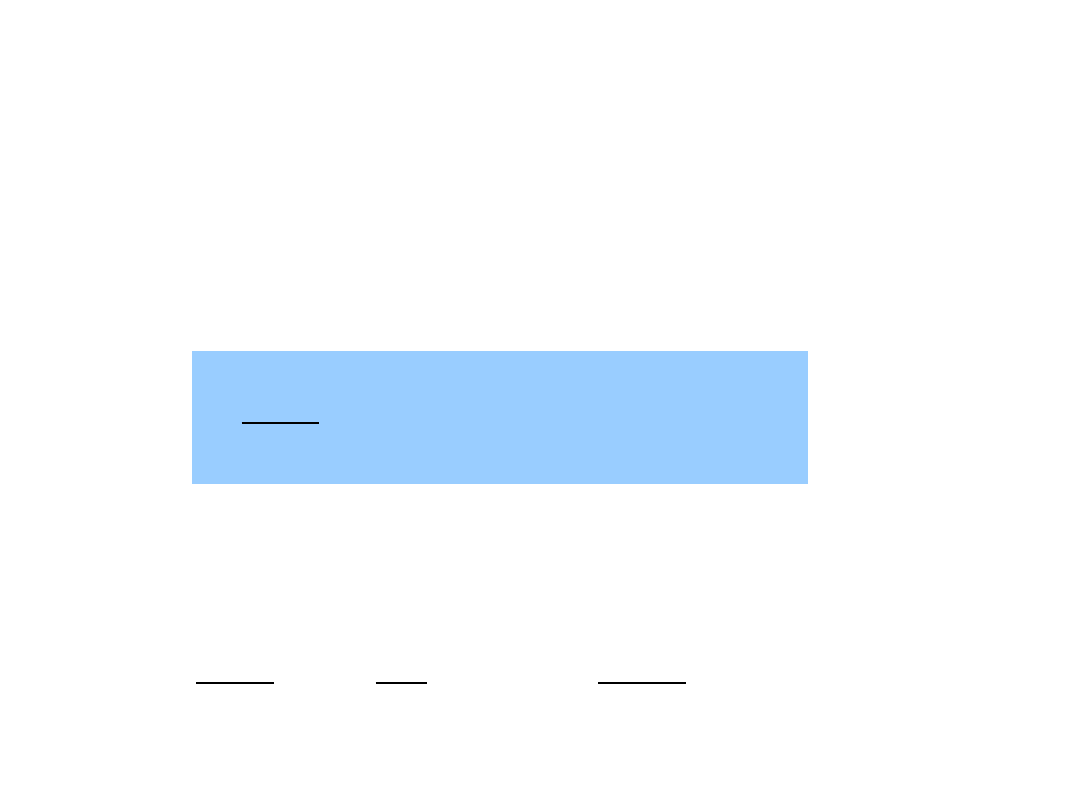
90

Drgania wymuszone tłumione

Równanie dynamiki ruchu:

t

F

v

cx

dt

x

d

m

x





cos

max

2

2









Po podstawieniach i przekształceniu:

Oprócz siły P

x

proporcjonalnej do wychylenia działa siła

oporu ruchu R

x

proporcjonalna do prędkości oraz siła F

x

będąca okresową funkcją czasu.

t

m

F

x

dt

dx

n

dt

x

d





cos

2

max

2

0

2

2







91

Pęd punktu materialnego

-

pęd punktu materialnego.

v

m



Wektor:

Gdy na punkt materialny nie działa żadna siła lub
działające siły się równoważą to pęd tego punktu
pozostaje stały.

Zasada zachowania pędu:

const

v

m

P











0

Z drugiej zasady dynamiki Newtona

i wzoru definicyjnego przyśpieszenia

wynika, że:

 

P

v

m

dt

d







P

a

m







dt

v

d

a







92

Zmiana pędu punktu materialnego w skończonym
przedziale czasu jest równa impulsowi siły działającej
na ten punkt w tym samym czasie.

Impuls siły





2

1

t

t

dt

P

S





Wielkość wektorowa charakteryzująca dynamiczne
skutki działania siły w skończonym przedziale czasu to
impuls siły:

)

(

)

(

1

2

2

1

v

m

v

m

v

m

v

m

d

S

mv

mv























Zasada zachowania pędu dla punktu materialnego ma
również zastosowanie dla środka ciężkości bryły sztywnej.

93

v

m

r

K

o











Moment pędu (kręt) punktu materialnego

-

moment pędu względem bieguna 0.

z

y

x

o

mv

mv

mv

z

y

x

k

j

i

K











Moment pędu względem danej osi jest równy składowej
na tę oś momentu pędu względem bieguna 0.













y

v

x

v

m

K

x

v

z

v

m

K

z

v

y

v

m

K

x

y

oz

z

x

oy

y

z

ox













rmv

K

o



Jeśli

,to:

v

r







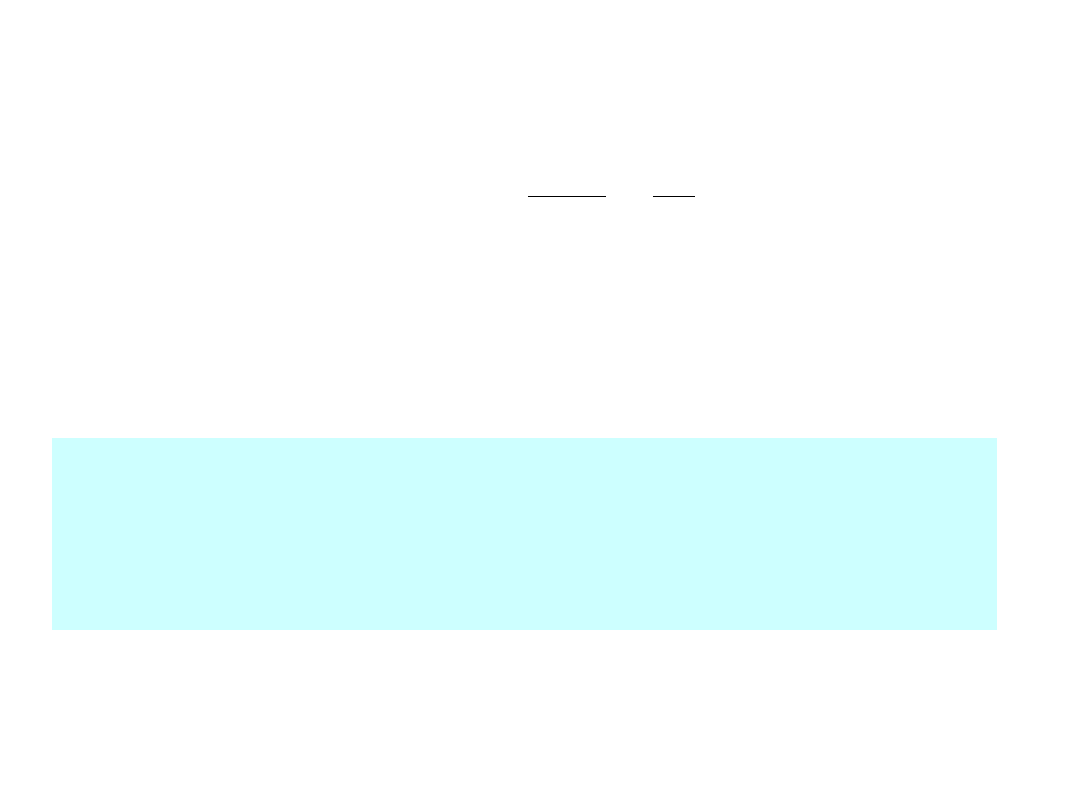
94





o

o

M

v

m

r

dt

d

dt

K

d















Zasada zachowania momentu pędu

-

moment siły P względem bieguna 0.

Pochodna momentu pędu względem bieguna równa jest
momentowi wypadkowej siły względem tego bieguna.

P

r

M

o











Zasada zachowania momentu pędu:
Jeżeli moment wypadkowej siły zewnętrznej względem
bieguna jest równy zeru, to moment pędu względem tego
bieguna pozostaje stały.
Moment pędu bryły sztywnej względem bieguna w ruchu
postępowym jest równy momentowi pędu środka ciężkości
bryły względem tego bieguna.

Pochodna momentu pędu:

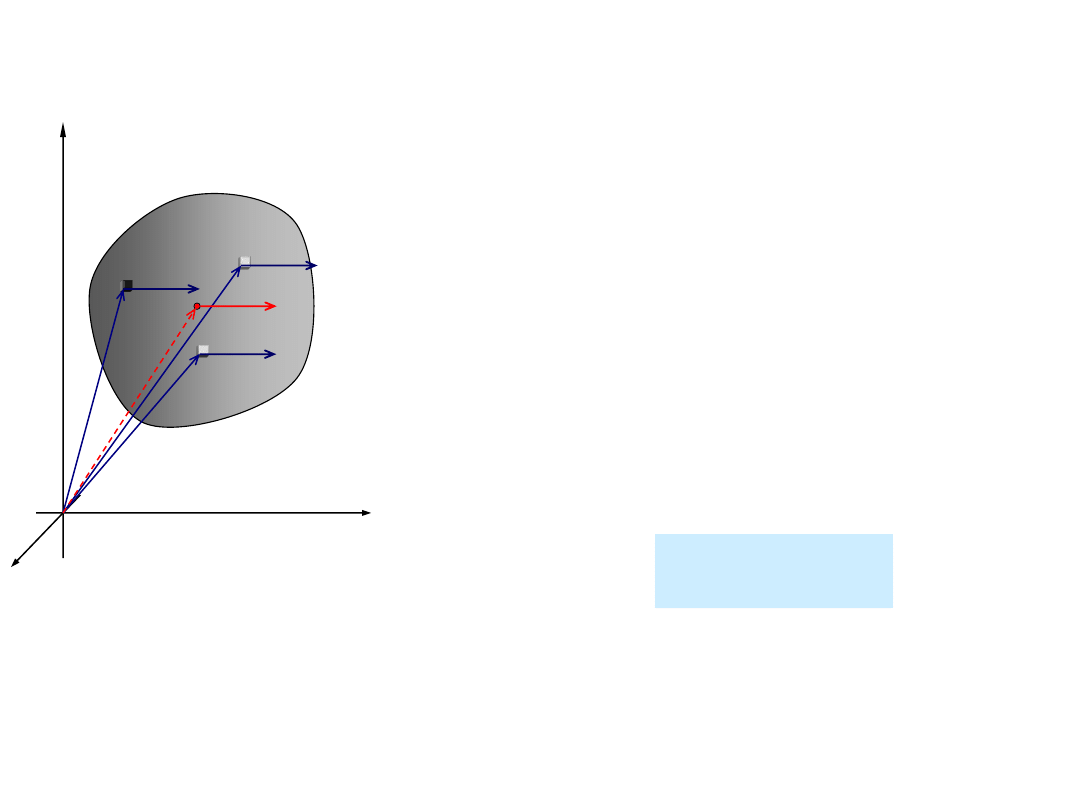
95

y

z

x

0

Moment pędu bryły sztywnej w ruchu postępowym

v

r

m

v

r

m

v

m

r

K

n

i

i

i

n

i

i

i

n

i

i

i



















































1

1

1

0

Wypadkowy moment pędu bryły
względem bieguna 0:

Stąd:

v

r

M

K

c











0

Wniosek: moment pędu bryły względem bieguna w ruchu
postępowym jest równy momentowi pędu środka masy bryły
względem tego bieguna.

v

m

2

r

2

r

1

m

1

v

m

i

r

i

v

M

r

c

v

c

n

i

i

i

r

M

r

m











1

Z definicji środka masy:

v

M

r

K

c











0

96

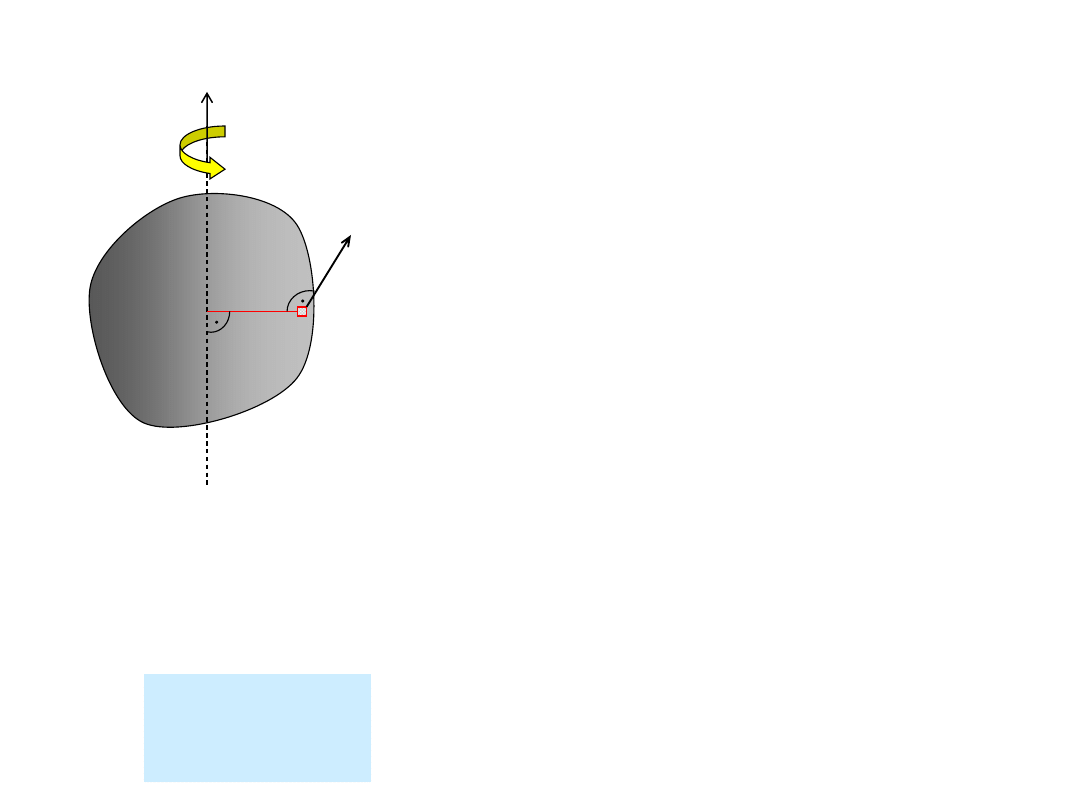
Moment pędu bryły sztywnej w ruchu obrotowym

h

dm

v



z

h

v





Prędkość liniowa elementu dm:

Moment pędu elementu dm
względem osi z:

dm

h

v

dm

h

dK

z

2











Całkowity moment pędu bryły
względem osi z:







z

M

M

z

J

dm

h

dm

h

K











2

2





M

z

dm

h

J

2

-

moment bezwładności bryły

względem osi z

M

97

Przykład 1: Obliczyć moment bezwładności jednorodnego pręta o masie m
i długości

l

względem osi przechodzącej przez jego: a) środek, b) koniec.

Przykład 2: Obliczyć moment bezwładności jednorodnego walca o masie
m i promieniu R względem jego osi symetrii.

0

z

x

dx

x

l

dx

l

m

dm



12

2

2

/

2

/

2

2

ml

dx

x

l

m

dm

x

J

l

l

m

z













3

2

0

2

2

ml

dx

x

l

m

dm

x

J

m

l

z











a)

0

z

x

dx

x

l

b)

Twierdzenie Steinera

: moment bezwładności bryły względem dowolnej osi

jest równy sumie momentu bezwładności bryły względem osi równoległej
przechodzącej przez środek masy bryły oraz iloczynu masy bryły i kwadratu
odległości między tymi osiami.

98

Równanie dynamiki bryły sztywnej w ruchu obrotowym

z

z

M

dt

dK



-

suma wszystkich momentów względem osi z.







n

i

iz

z

M

M

1

Pochodna momentu pędu względem osi z:



z

z

J

K



-

moment pędu bryły względem osi z.

 

dt

d

J

J

dt

d

z

z







-

dla bryły sztywnej J

z

= const.

z

z

M

dt

d

J





-

równanie dynamiki bryły

99

2

2

1

mv

E



Energia kinetyczna

- energia kinetyczna punktu materialnego







n

i

i

i

v

m

E

1

2

2

-

energia kinetyczna układu n punktów

materialnych

2

2

mv

E



-

energia kinetyczna ciała sztywnego

poruszającego się ruchem postępowym

100

Energia kinetyczna bryły sztywnej w ruchu obrotowym

2

2

1

v

dm

dE





h

dm

v



z

Energia kinetyczna elementu dm:

Stąd:

Całkowita energia kinetyczna bryły:









dm

v

dE

E

2

2

1





dm

h

J

z

2

-

moment bezwładności bryły

względem osi z

z

J

E

2

2

1





const

h

v









,

Prędkość liniowa elementu dm:









dm

h

dm

h

E

2

2

2

1

2

2

2

1





101

Energia kinetyczna bryły sztywnej w ruchu złożonym

2

2

2

2



z

c

J

mv

E





v

c

– prędkość chwilowa środka masy bryły sztywnej,

J

z

– moment bezwładności bryły względem osi

chwilowego obrotu, przechodzącej przez środek masy,



-

chwilowa prędkość kątowa wokół osi chwilowego

obrotu.

Ruch złożony bryły sztywnej – złożenie:
-

ruchu krzywoliniowego środka masy bryły z prędkością

chwilową v

c

-

ruchu obrotowego z prędkością kątową



wokół chwilowej

osi, przechodzącej przez środek masy bryły.

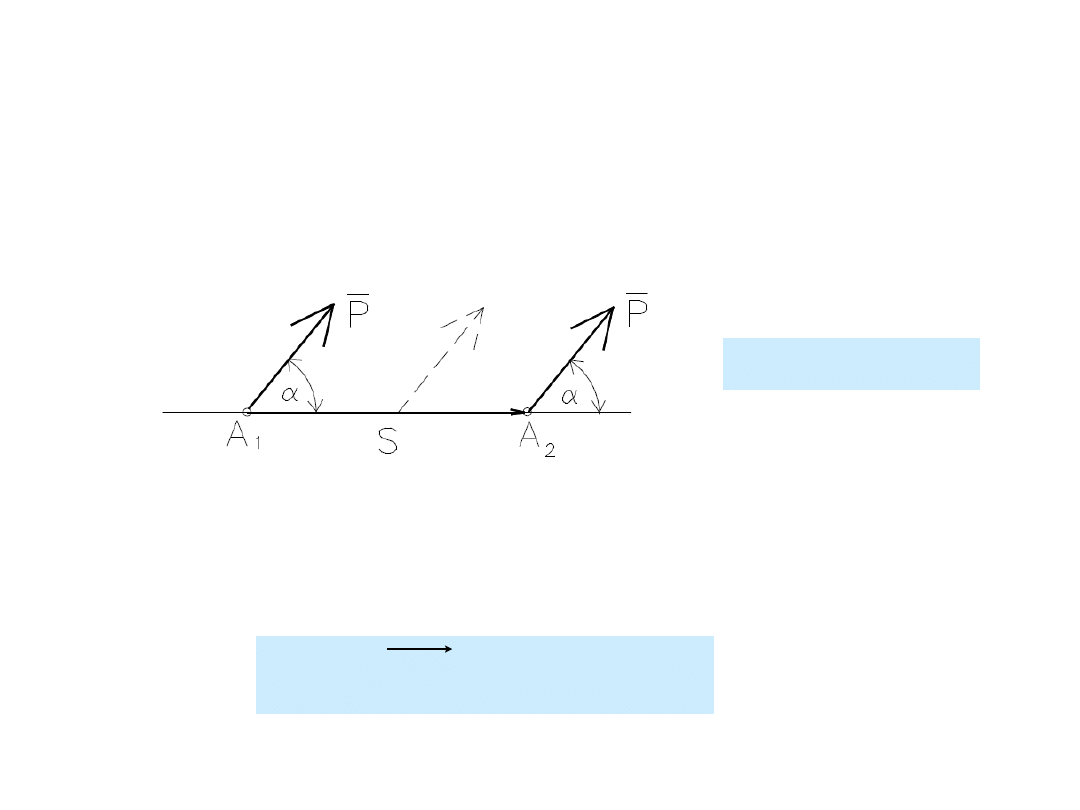
102



cos

Ps

L



Praca siły

Pracą siły stałej na prostoliniowym przesunięciu punktu
przyłożenia tej siły nazywa się iloczyn bezwzględnej wartości
przesunięcia i miary rzutu siły na kierunek przesunięcia.



cos

2

1











s

P

A

A

P

L



Wartość liczbowa pracy jest równa iloczynowi skalarnemu
wektora siły i wektora przesunięcia.



cos

P

s

L





103





z

y

x

P

P

P

P

,

,





W układzie współrzędnych prostokątnych:

s

P

s

P

s

P

s

P

s

P

L

n

n

i

i



























































...

2

1

1

Praca wypadkowej sił przyłożonych do jednego punktu jest
równa sumie prac poszczególnych sił:

]

,

,

[

z

y

x

s

s

s

s





z

z

y

y

x

x

s

P

s

P

s

P

s

P

L















104

Jeśli punkt przyłożenia siły opisuje odcinek toru
krzywoliniowego, to:

Składowe P

x

, P

y

, P

z

mogą zależeć od czasu i każdej ze

współrzędnych położenia.



















2

1

2

1

A

A

z

y

x

A

A

dz

P

dy

P

dx

P

r

d

P

L





Praca w ruchu obrotowym

Praca siły w ruchu obrotowym równa jest iloczynowi momentu
siły względem osi obrotu i kąta obrotu ciała.



l

M

L



105

Siły zachowawcze

Praca wykonana nad punktem materialnym przez siły
zachowawcze nie zależy od kształtu toru a tylko od położenia
punktu początkowego i końcowego.

Praca wykonana przez te siły po dowolnej drodze zamkniętej
jest równa zeru.

Pole zachowawcze sił – przestrzeń, w której działają siły
zachowawcze.

Przykład siły zachowawczej – siła ciężkości.
Przykłady sił niezachowawczych – siła tarcia, siła oporu
aerodynamicznego.

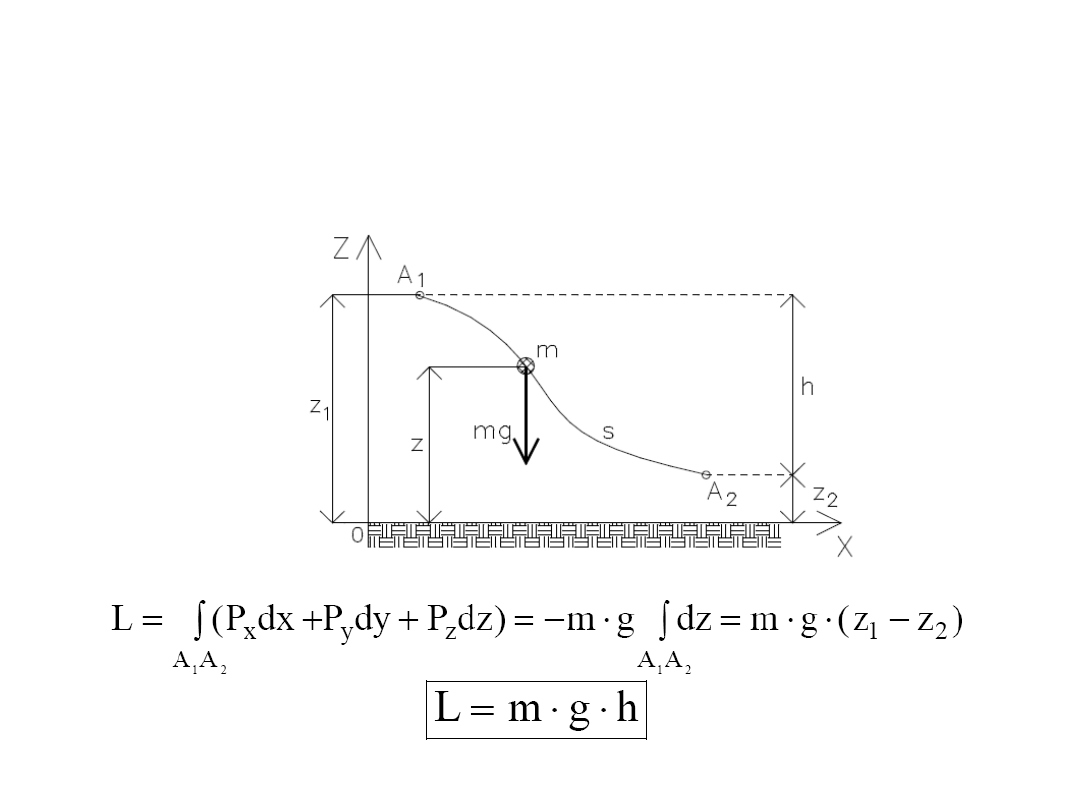
106

Energia potencjalna

Praca wykonana przez siły ciężkości nie zależy od kształtu
toru a jedynie od różnicy wysokości nad umownym poziomem
odniesienia.

0

P

P

g

m

P

x

y

z











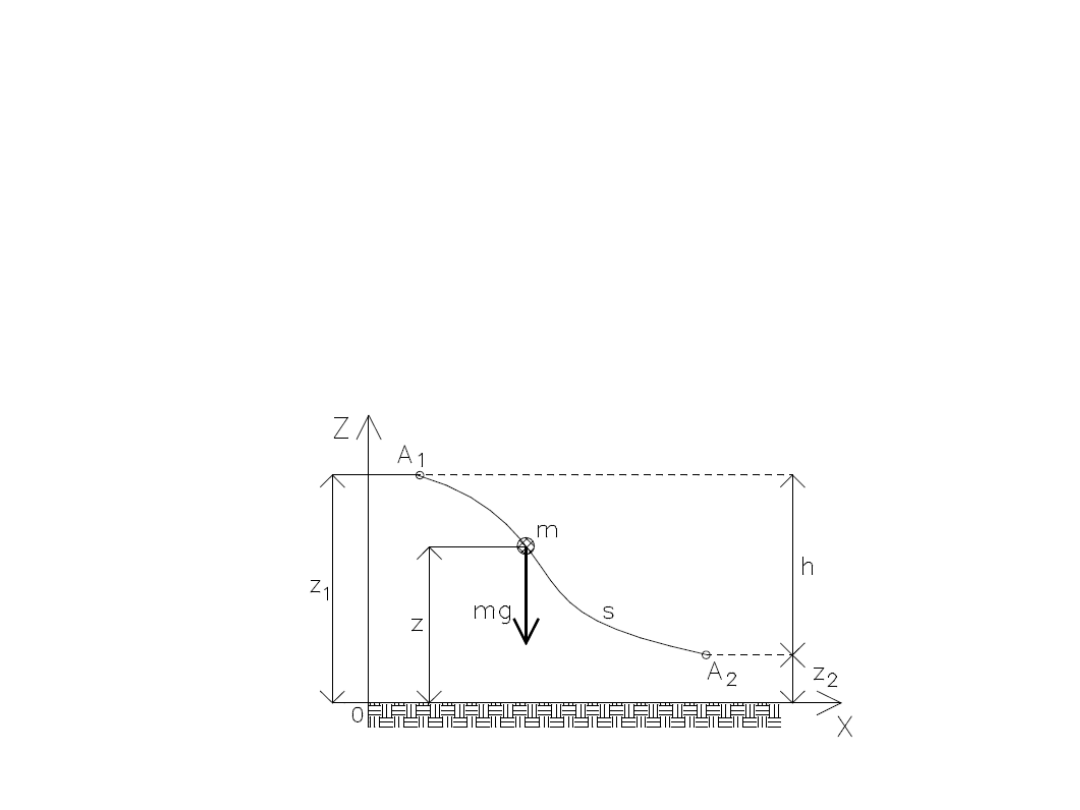
107

Energia potencjalna punktu materialnego jest to praca,
jaką może wykonać nad punktem materialnym siła ciężkości
w jednorodnym polu zachowawczym sił ciężkości.

mgh

z

z

mg

V







)

(

2

1

h

– różnica poziomów między punktem początkowym a

końcowym.

108

Energia mechaniczna

Energia mechaniczna

punktu materialnego jest sumą jego

energii kinetycznej i energii potencjalnej.

Zasada zachowania energii mechanicznej:

Podczas ruchu punktu materialnego w zachowawczym polu
sił, suma jego energii kinetycznej i potencjalnej, zwana
energią mechaniczną, jest wielkością stałą:

const





V

E

Równoważność pracy i energii kinetycznej:

Przyrost energii kinetycznej punktu materialnego w
skończonym przedziale czasu jest równy sumie prac, które
wykonały w tym czasie wszystkie siły zewnętrzne działające
na ten punkt:

L

E

E





1

2

109

Przykład 1: Punkt materialny o masie m porusza się w polu zachowawczym
sił ciężkości. Wyznaczyć prędkość tego punktu na wysokości z, jeśli jego
prędkość na wysokości z

0

wynosi v

0

.

Przykład 2: Wahadło matematyczne (punkt materialny zawieszony na nici)
wychylono z położenia równowagi o kąt



=



/2 i puszczono swobodnie.

Wyznaczyć prędkość liniową punktu oraz siłę naciągu nici w funkcji kąta



.

Przykład 3: Jednorodny krążek o promieniu R i masie m toczy się po
poziomej prostej bez poślizgu, z prędkością liniową środka masy równą v

0

.

Obliczyć energię kinetyczną krążka.





z

z

g

v

v







0

2

0

2

Odp.



cos

2

Odp.

gl

v





cos

3mg

S



2

0

4

3

Odp.

mv

E



110

Wytrzymałość materiałów

„Wytrzymałość” materiału – właściwość ciała stałego
polegająca na przeciwstawianiu się niszczącemu
działaniu sił zewnętrznych.

W materiale poddanym działaniu sił zewnętrznych
(obciążeń) powstają siły wewnętrzne, będące
wynikiem oddziaływania pomiędzy poszczególnymi
cząstkami ciała jednorodnego.

111

Wytrzymałość materiałów posługuje się modelem
ciała jednorodnego, izotropowego i idealnie
sprężystego.

Ciało jednorodne – ciało, w którym materia wypełnia
jego objętość w sposób ciągły.

Materiał izotropowy – materiał, którego właściwości są
takie same we wszystkich kierunkach.

Odkształcenia sprężyste – odkształcenia, które
ustępują po usunięciu obciążeń.

Uproszczenia i uogólnienia

112

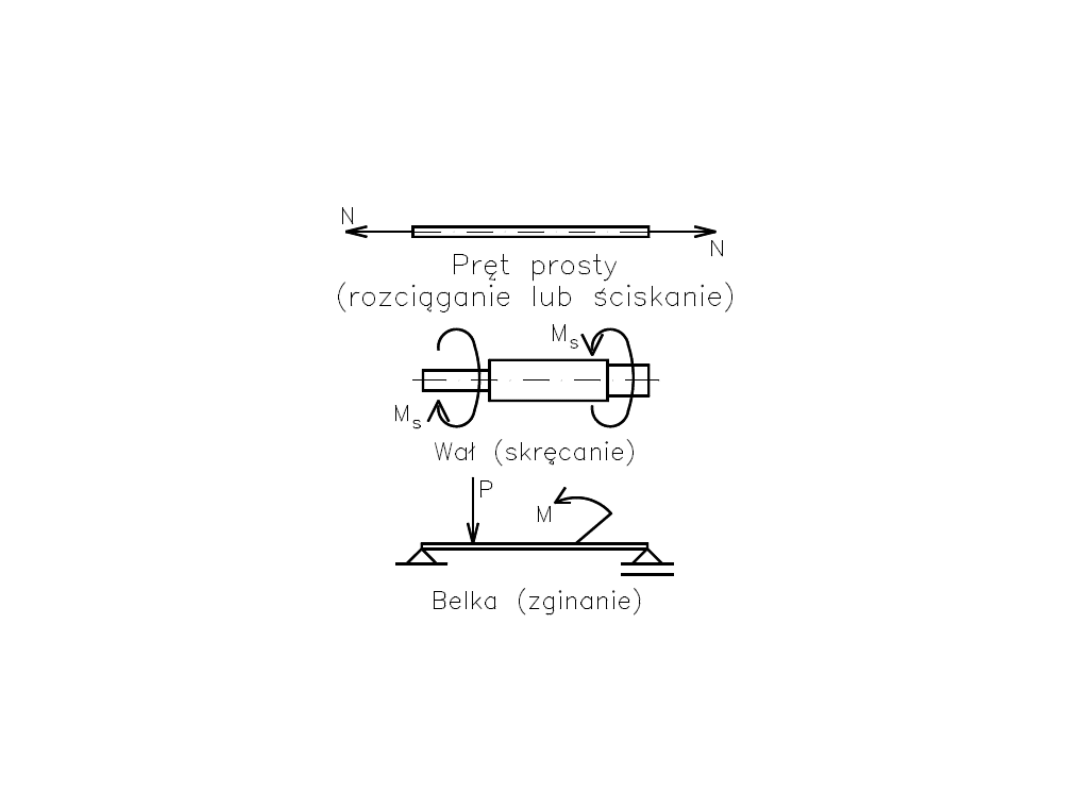
Modele nominalne

w wytrzymałości materiałów:

-

pręt

-

wał

- belka

113

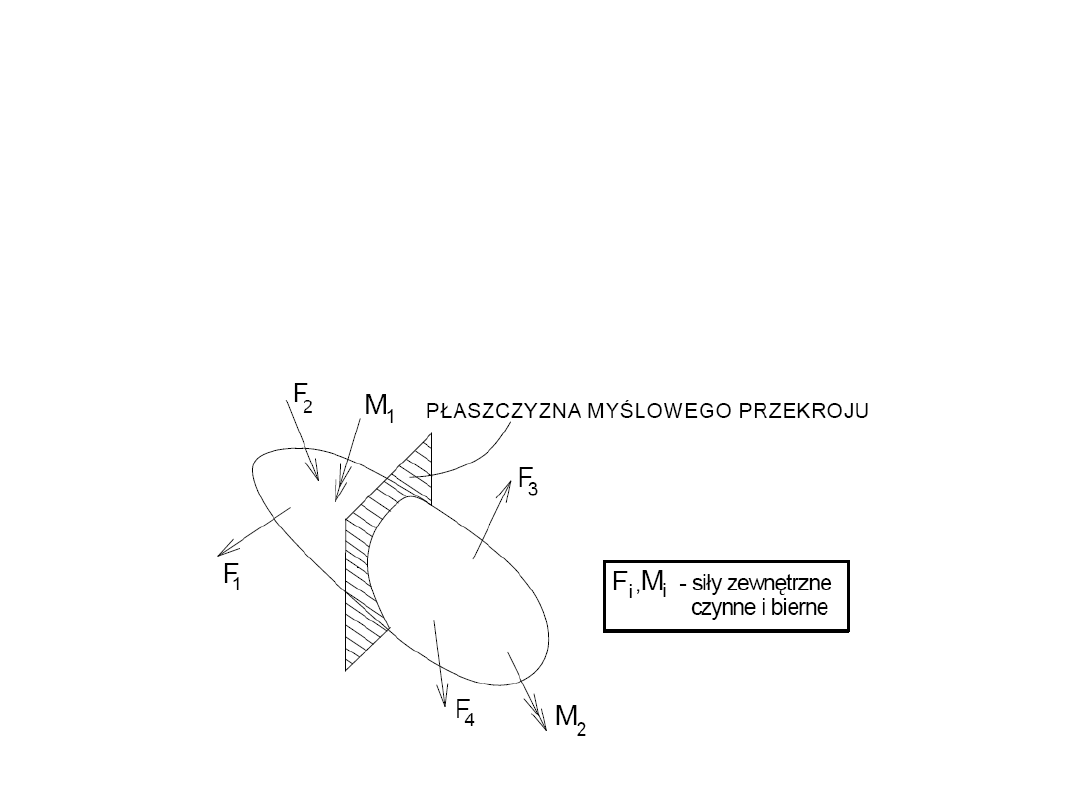
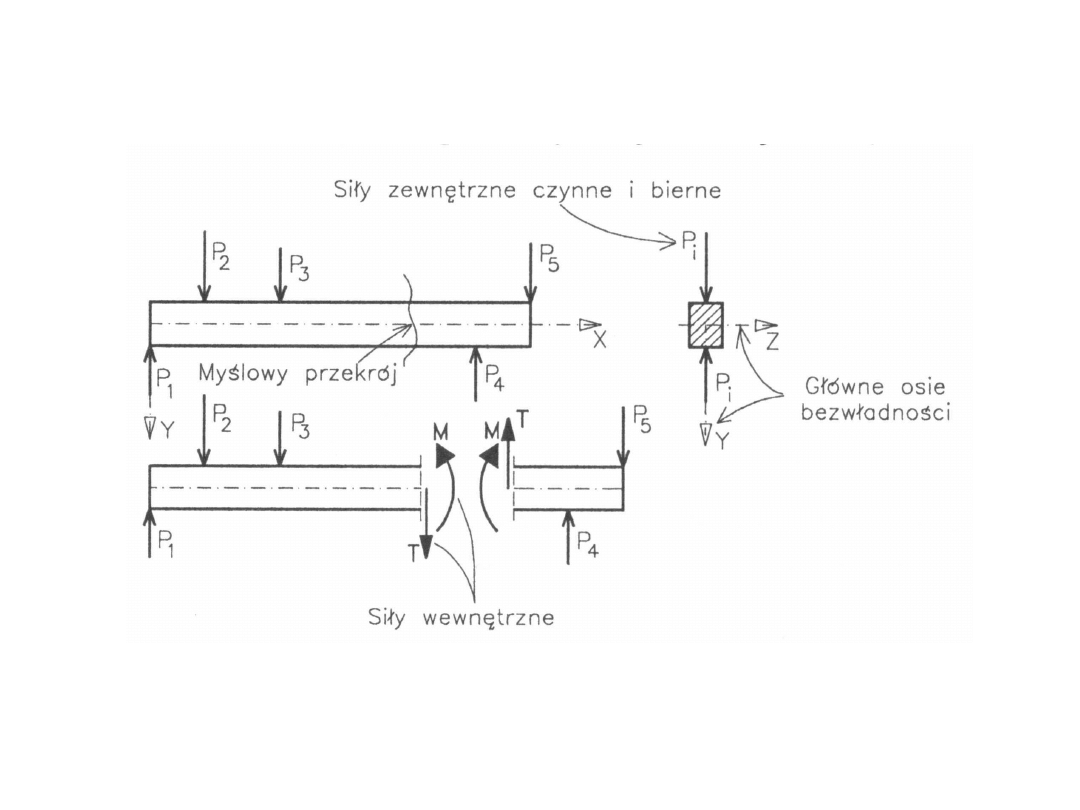
Dla ujawnienia sił wewnętrznych korzysta się z zasady
myślowych przekrojów.

Siły wewnętrzne są wynikiem oddziaływania jednej części
ciała oddzielonej myślowym przekrojem na drugą.

Obciążenia i siły wewnętrzne

114

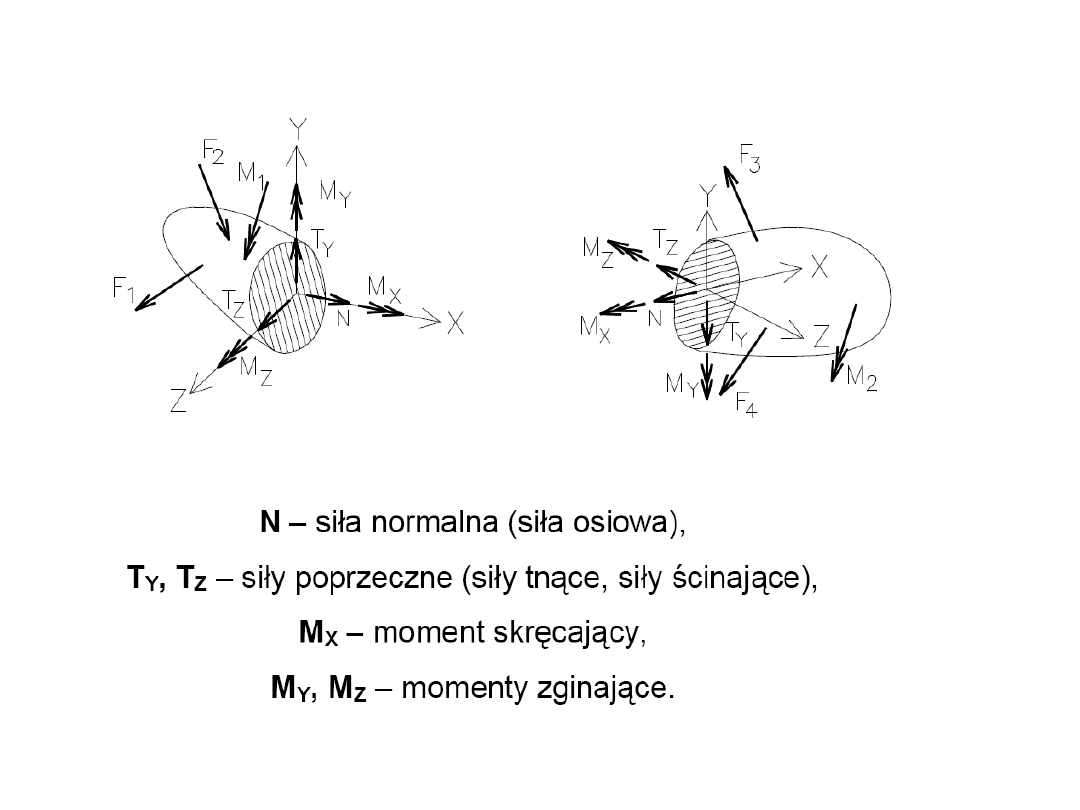
Siły wewnętrzne w myślowo podzielonym ciele

115

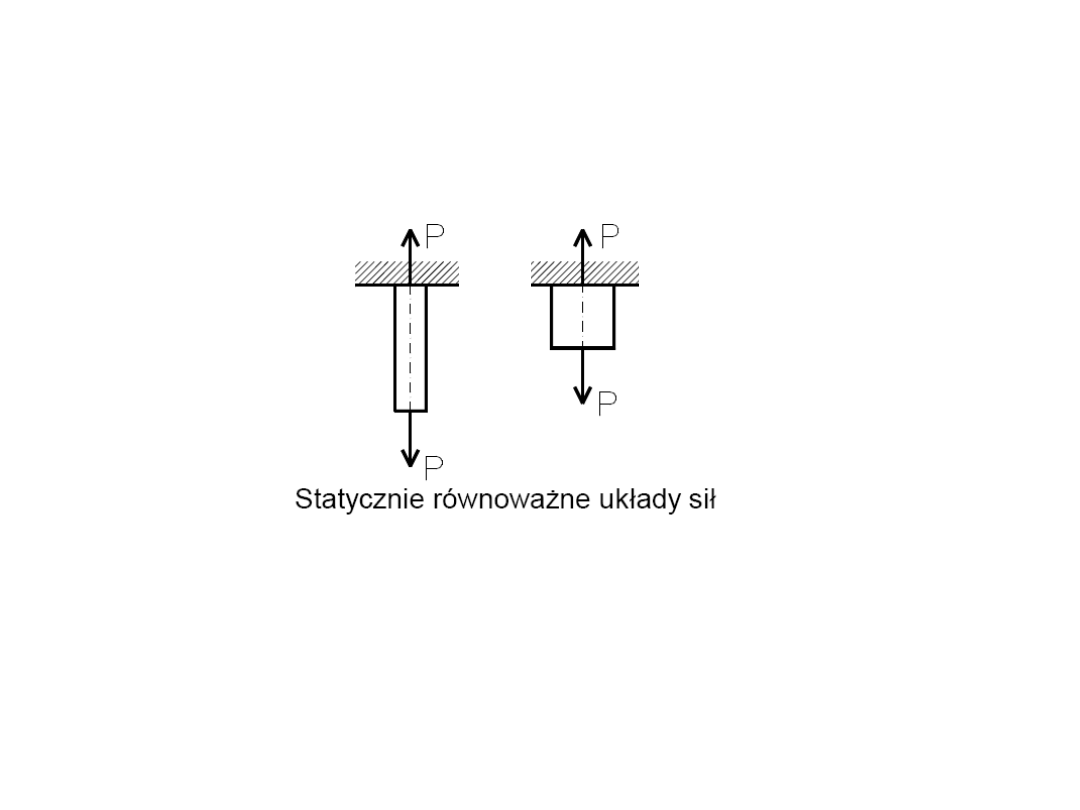
116

Układy sił równoważne z punktu widzenia statyki mogą się
charakteryzować różną wytrzymałością.

Do oceny wytrzymałości danej konstrukcji na zniszczenie
wprowadza się pojęcie naprężenia.

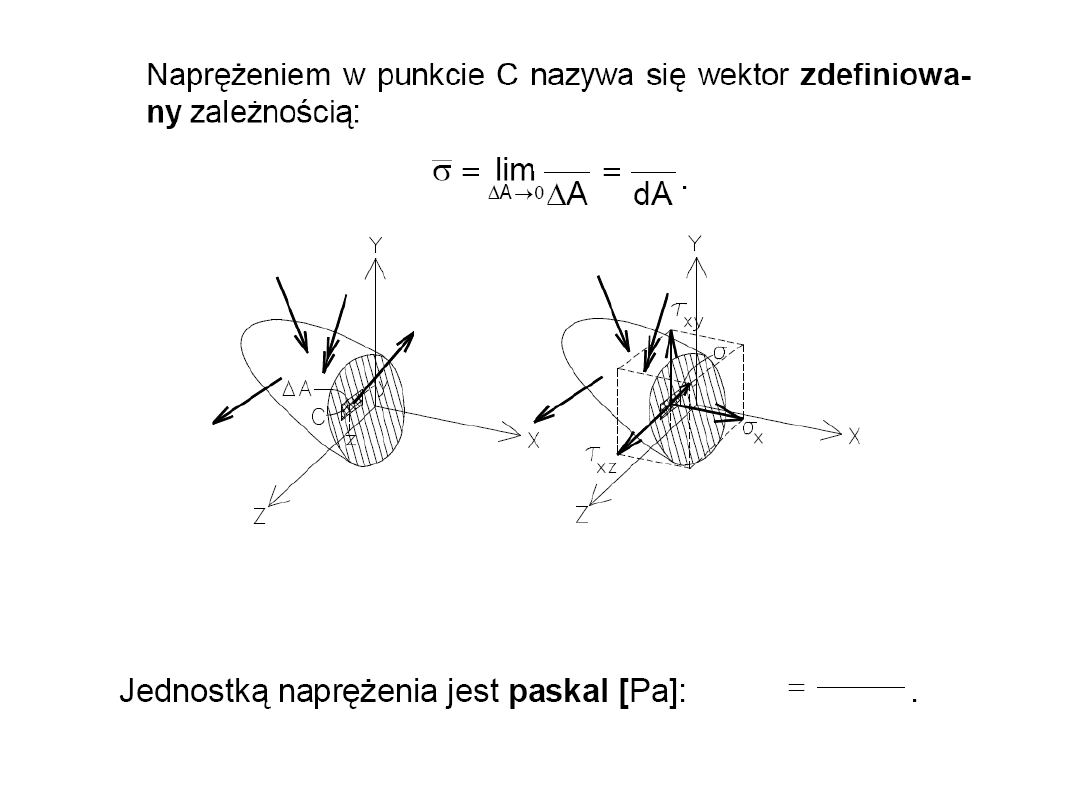
117



P

k

j

i

xz

xy

x

















1 Pa

1 N

1 m

2

dP



P

118

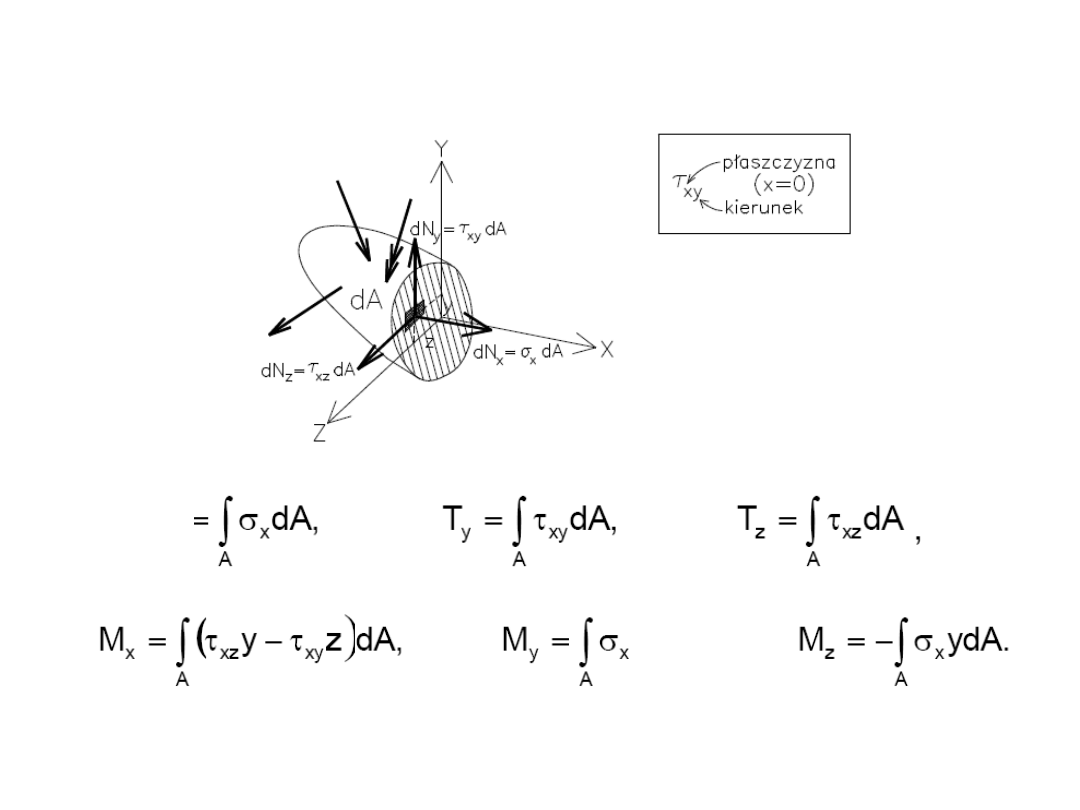
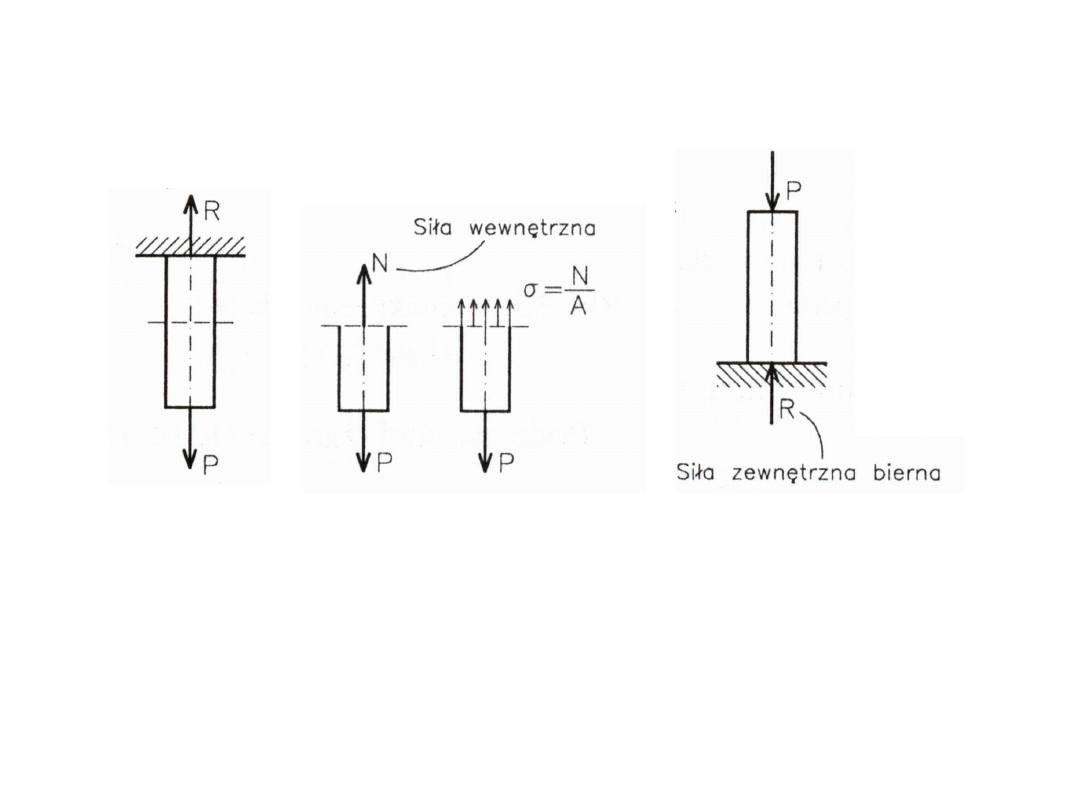
Związki między siłami wewnętrznymi i naprężeniami

zdA

N

119

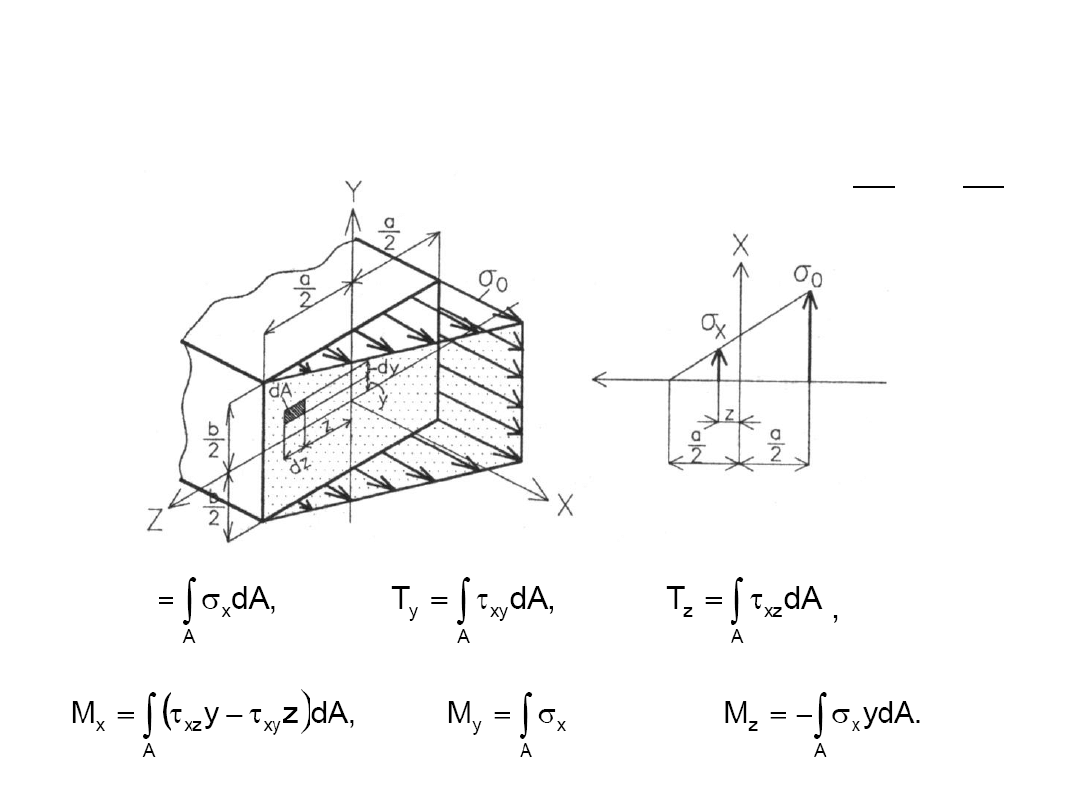
Przykład: Określić związki między siłami wewnętrznymi a naprężeniami,
jeśli naprężenia w przekroju prostokątnym rozłożone są jak na rysunku.
Dane: a, b,



0

.

0





xz

xy















 



a

z

x

2

1

2

0





zdA

N

120

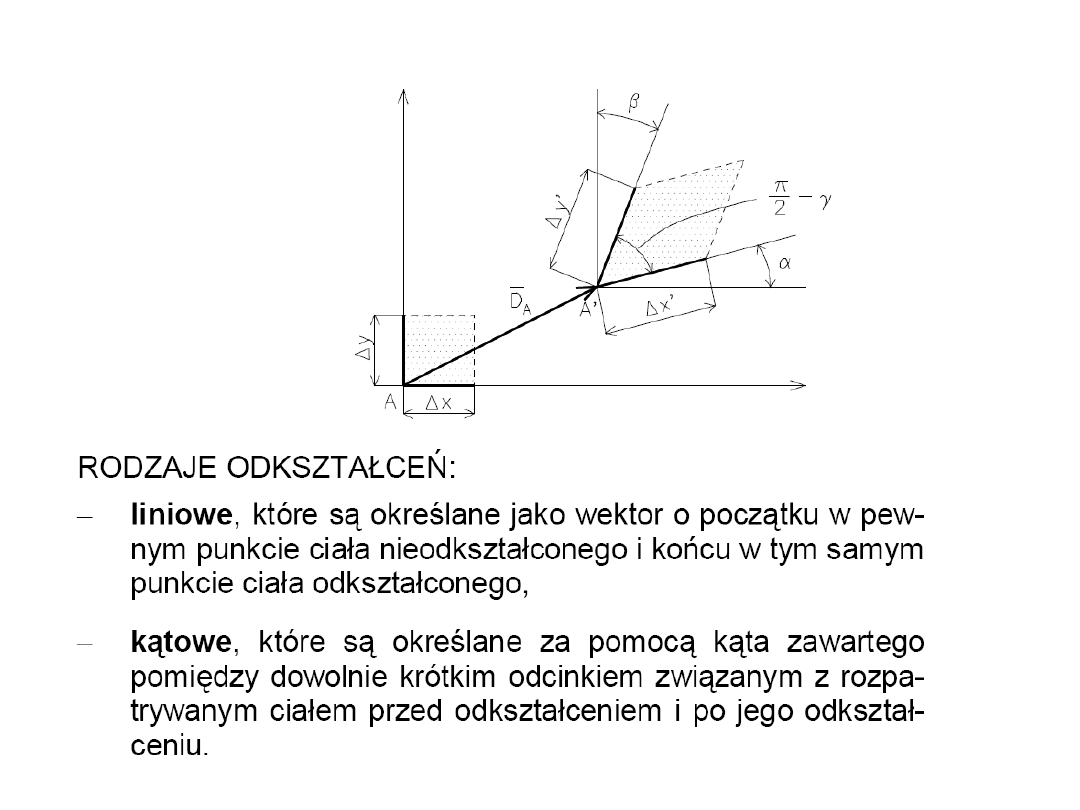
Odkształcenia i przemieszczenia

X

Y

121

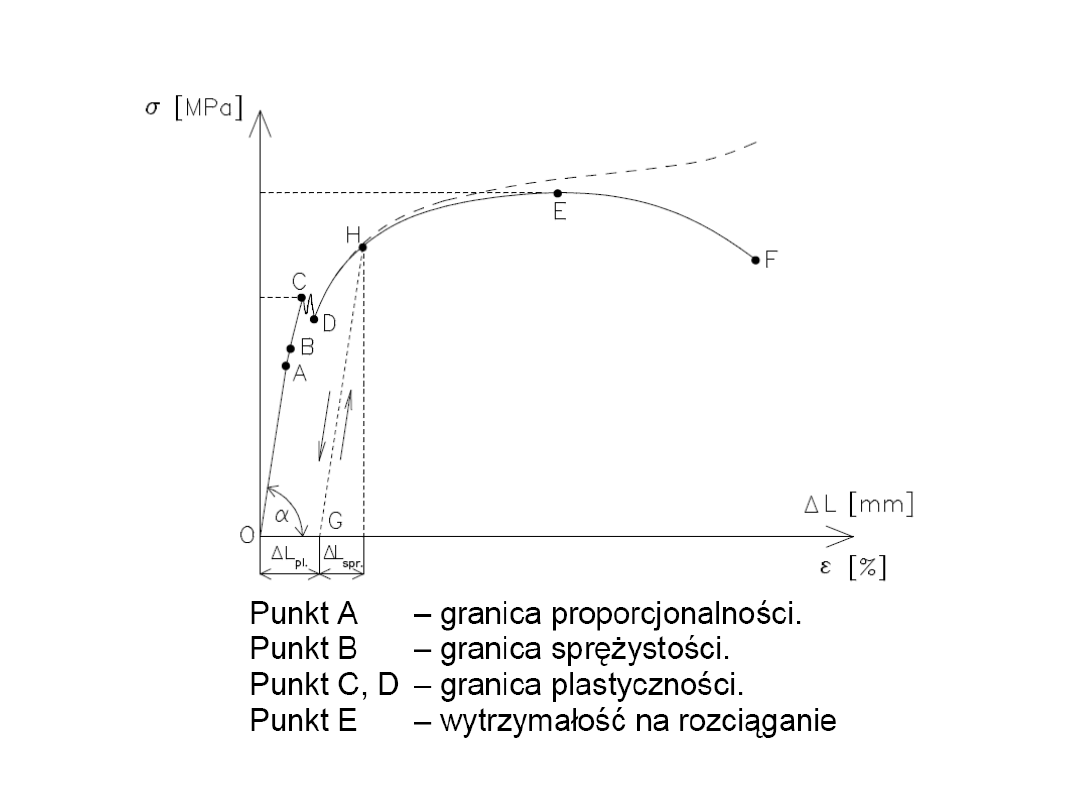
Wykres rozciągania próbki

(statyczna próba rozciągania)

P [kN]

P

m

P

e

123

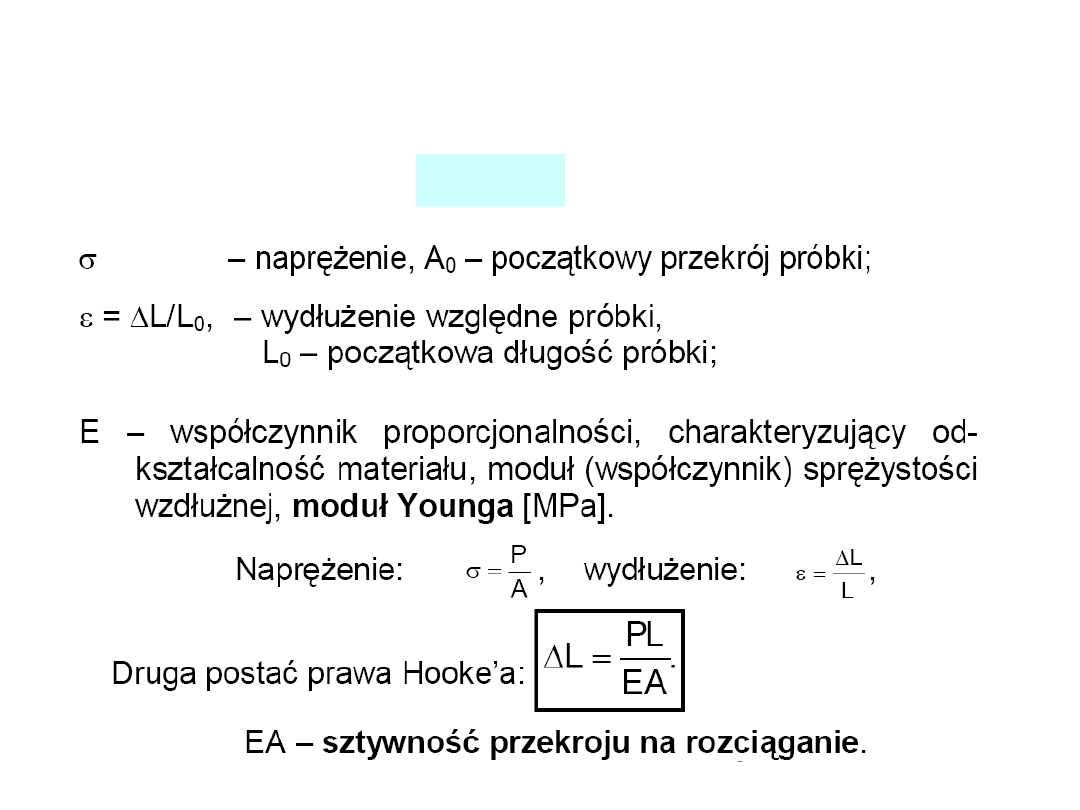
Dla naprężeń nie przekraczających granicy
proporcjonalności obowiązuje prawo Hooke’a





E



= P/A

0

124

Naprężenia dopuszczalne

n = 1,5



2,5

Jeśli konstrukcja ma bezpośredni związek z
bezpieczeństwem ludzi, to n = 5



10

125

Warunek wytrzymałościowy

Warunek sztywności

Warunek sztywności jest wykorzystywany do określenia wymiarów

konstrukcji ze względu na dopuszczalne odkształcenia

dop

l

l







dop







max

126

Siły zewnętrzne i wewnętrzne w prętach

Pręt rozciągany

Pręt ściskany

Siły zewnętrzne działają tylko wzdłuż osi pręta.
Siły rozciągające: znak „+”, siły ściskające: znak „-”

Suma sił zewnętrznych działających wzdłuż osi pręta
jest równa zeru.

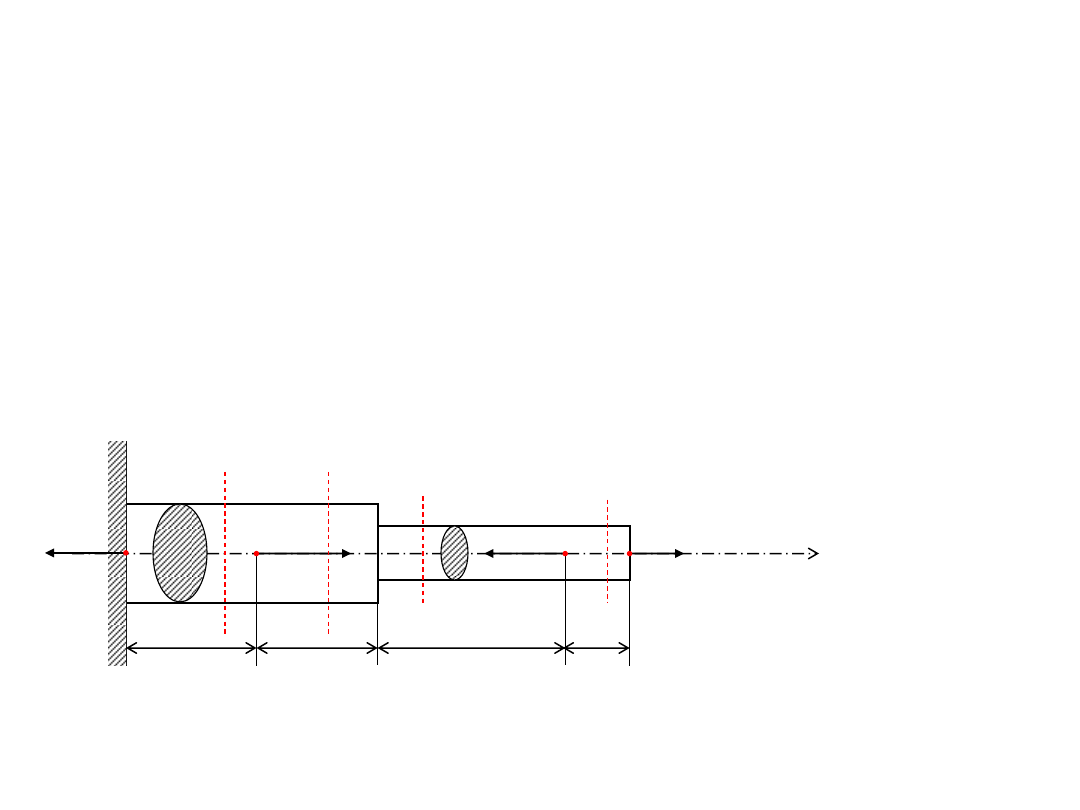
127

Siły wewnętrzne wyznacza się metodą myślowych przekrojów.

Myślowych przekrojów dokonuje się w dowolnych miejscach
odcinków, których granicami są punkty:
-

przyłożenia obciążenia,

-

zmiany kształtu poprzecznego pręta.

P

3

P

2

P

1

A

3

A

2

d

d

c

c

b

b

a

a

d

c

b

a

R

0

3

2

1









R

P

P

P

x

128

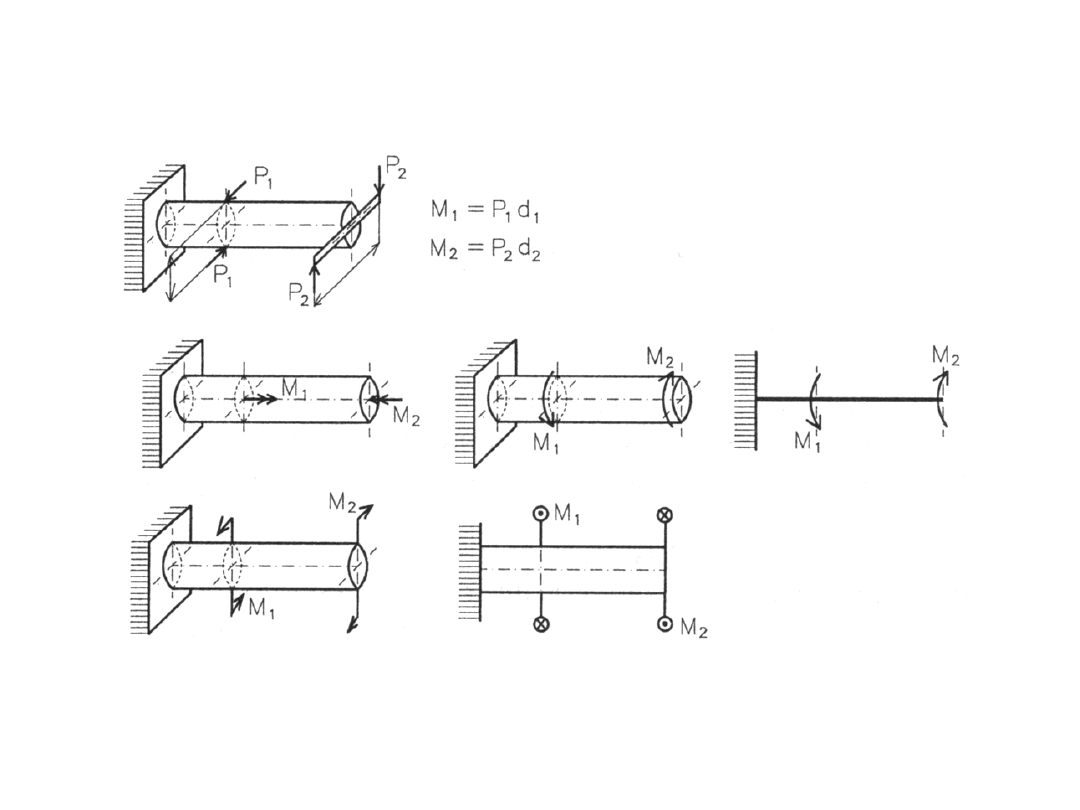
Skręcanie wałów o przekroju okrągłym

Sposoby zaznaczania momentów skręcających

129

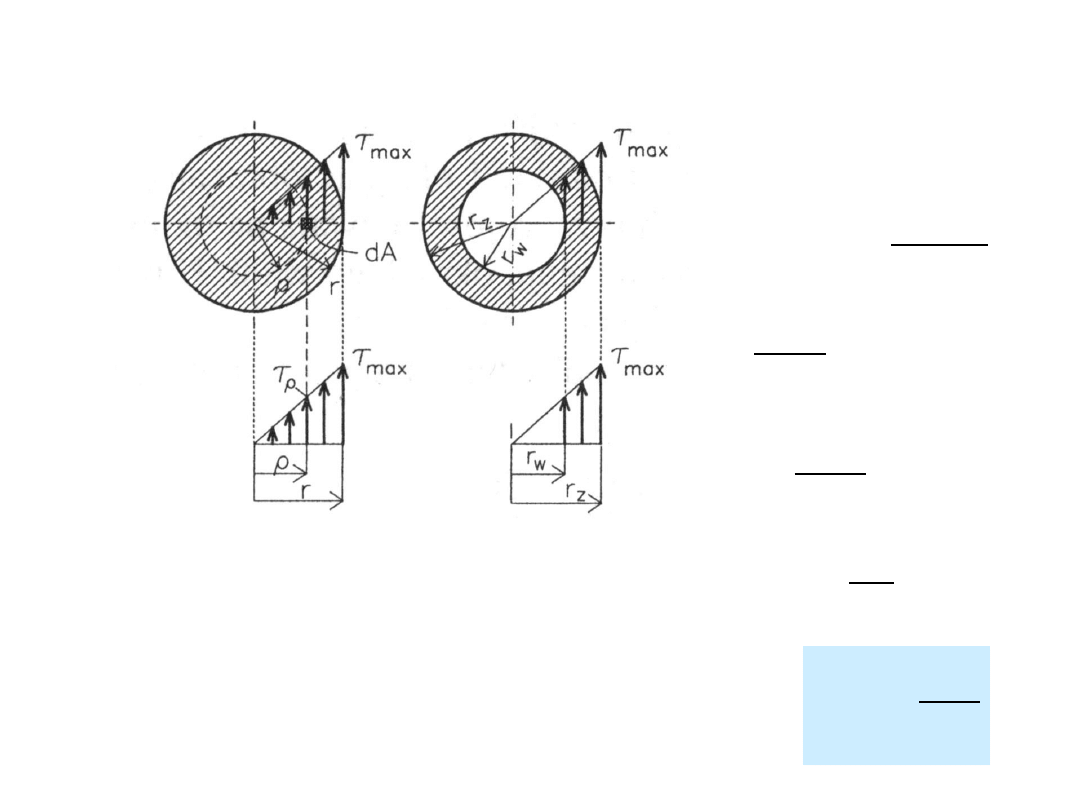
Rozkład naprężeń stycznych

wał pełny wał wydrążony

s

A

M

A





d







r









max



s

A

M

dA

r





2

max





J

0

– biegunowy moment bezwładności

W

0

– wskaźnik wytrzymałości przekroju na skręcanie

s

M

J

r



0

max



0

0

W

r

J



0

max

W

M

s





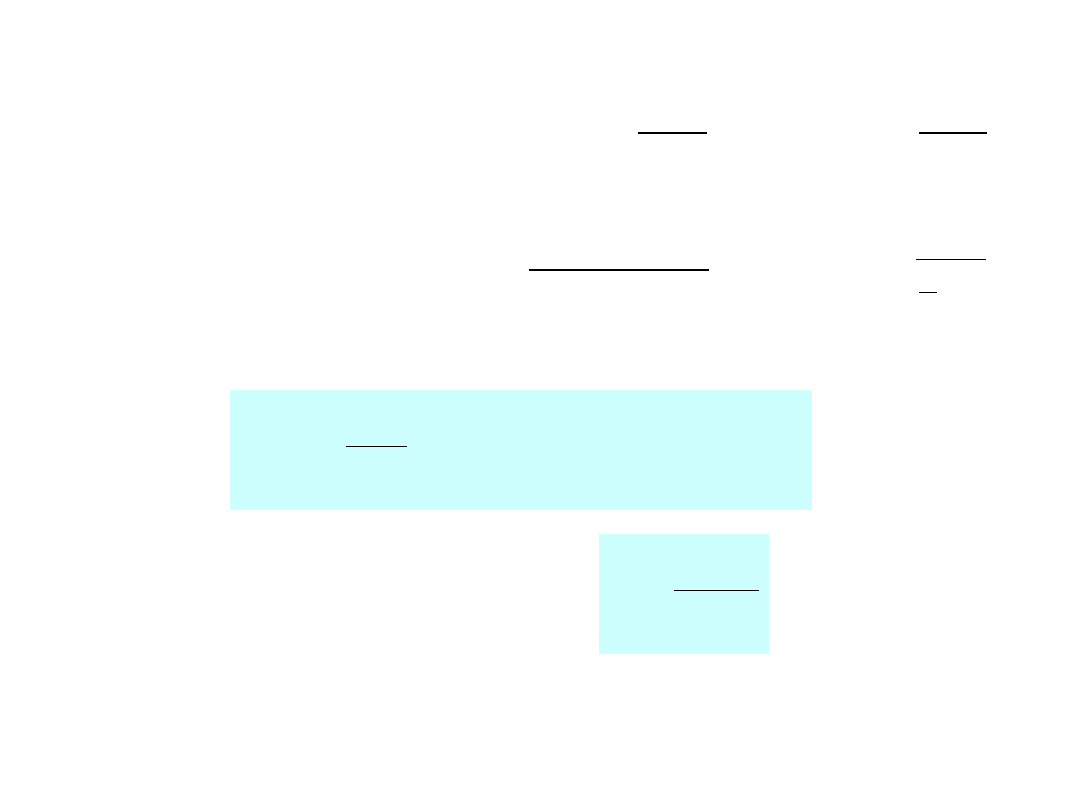
130

Dla pełnego wału okrągłego:

16

3

0

d

W





32

4

0

d

J





Dla wału wydrążonego:

z

d

J

W

2

1

0

0







32

4

4

0

w

z

d

d

J







Warunek wytrzymałościowy na skręcanie:

dop

dop

dop

s

W

M









5

,

0

,

0

max







Kąt skręcania wału o długości L:

0

GJ

L

M

s





G

– moduł odkształcenia postaciowego (moduł Kirchhoffa)

131

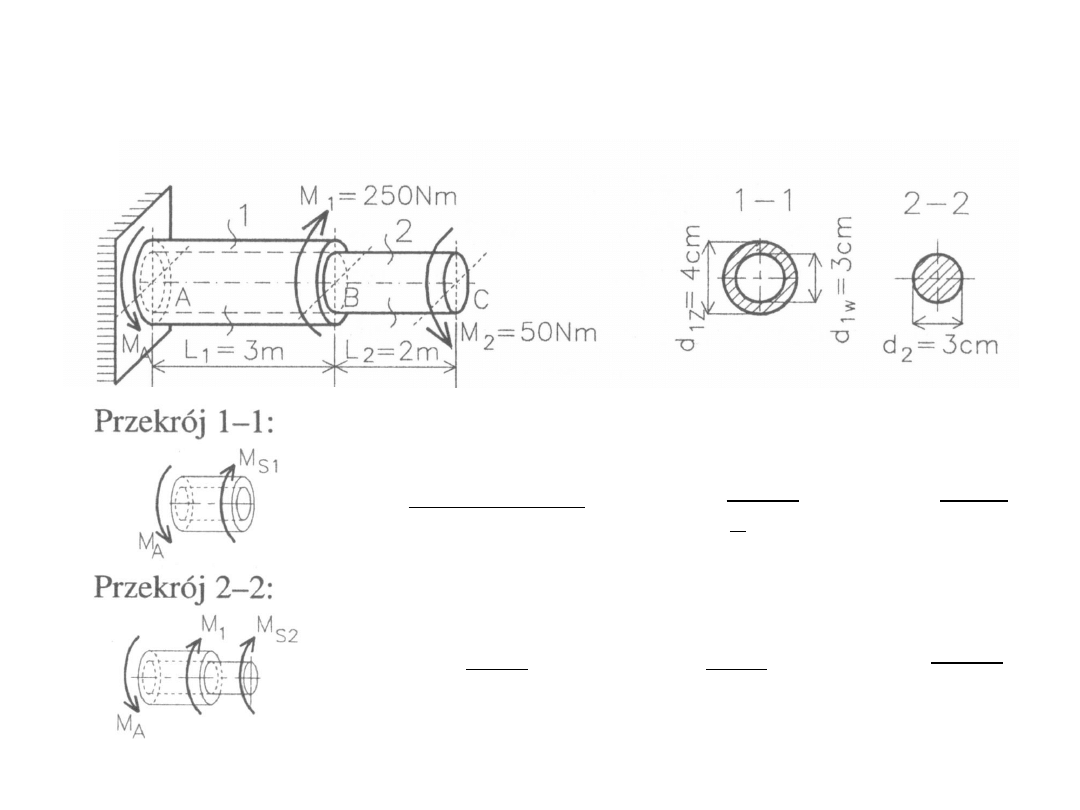
Przykład: Wyznaczyć momenty wewnętrzne i naprężenia styczne w

wale jak na rysunku.





32

4

1

4

1

01

w

z

d

d

J







z

d

J

W

1

2

1

01

01



32

4

2

02

d

J





16

3

2

02

d

W





01

1

W

M

S

AB





02

2

W

M

S

BC





132

Zginanie belek prostych

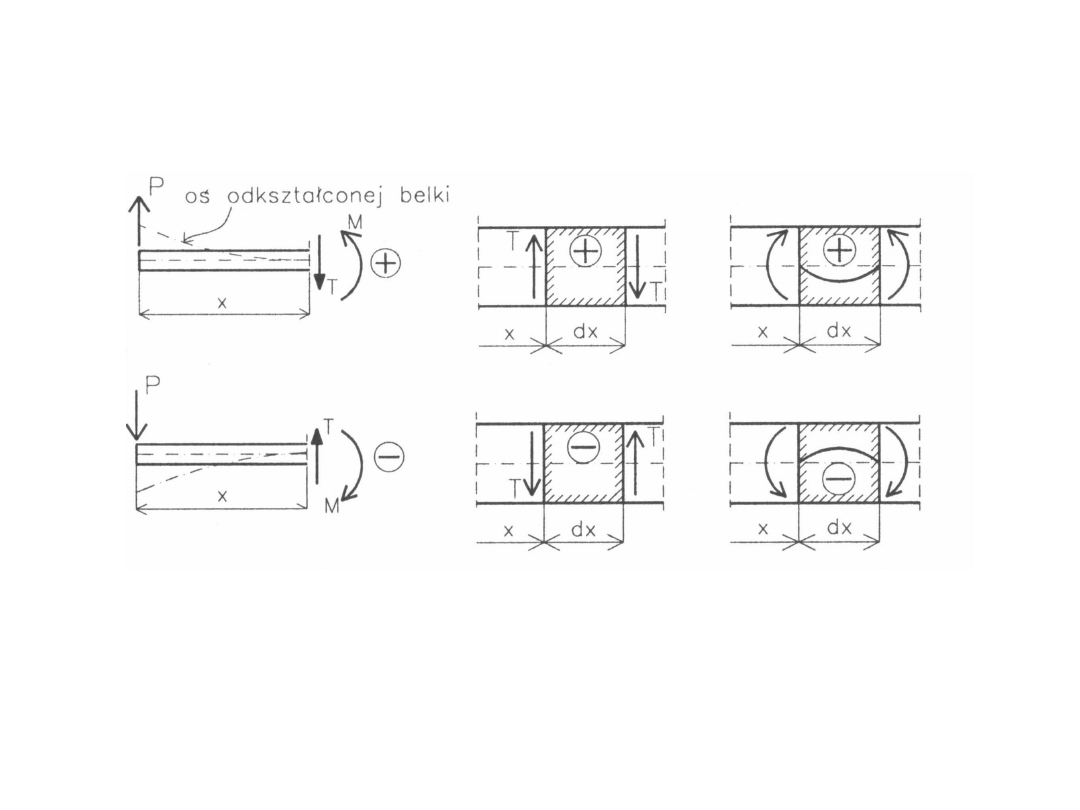
133

Umowne określenie znaków sił wewnętrznych

134

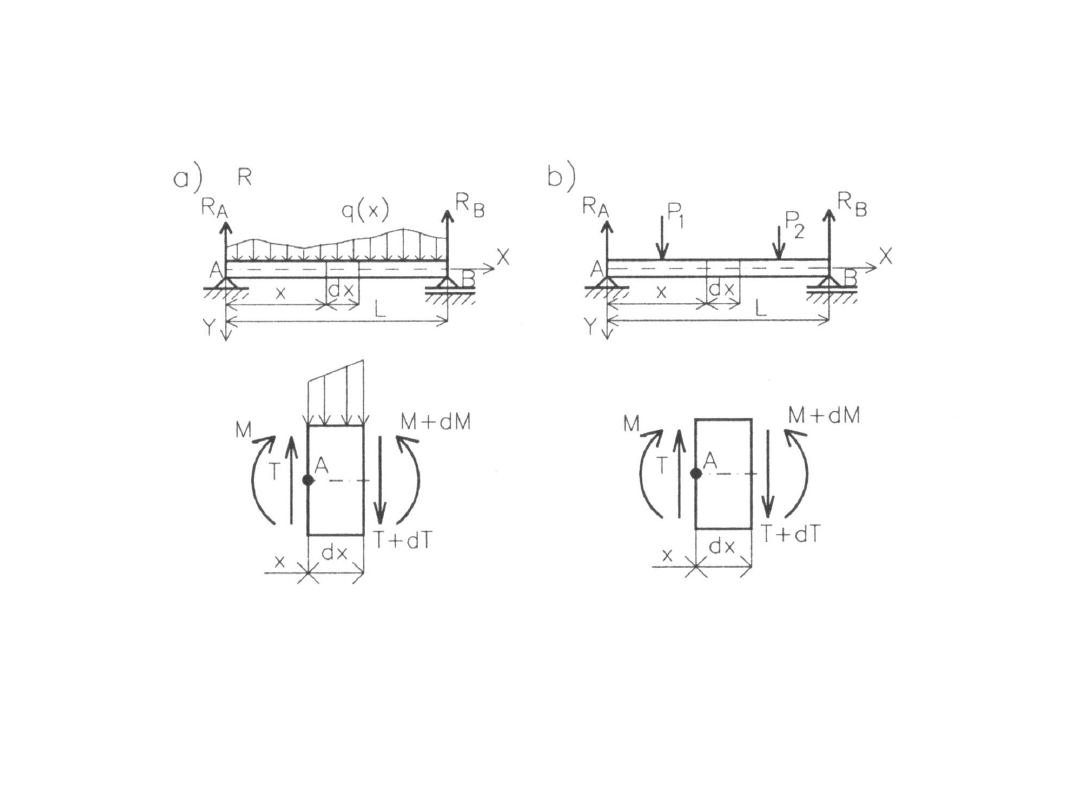
Zależności między obciążeniami a siłami wewnętrznymi

a)

belka obciążona siłami ciągłymi o intensywności q (x)

b)

belka obciążona siłami skupionymi

135

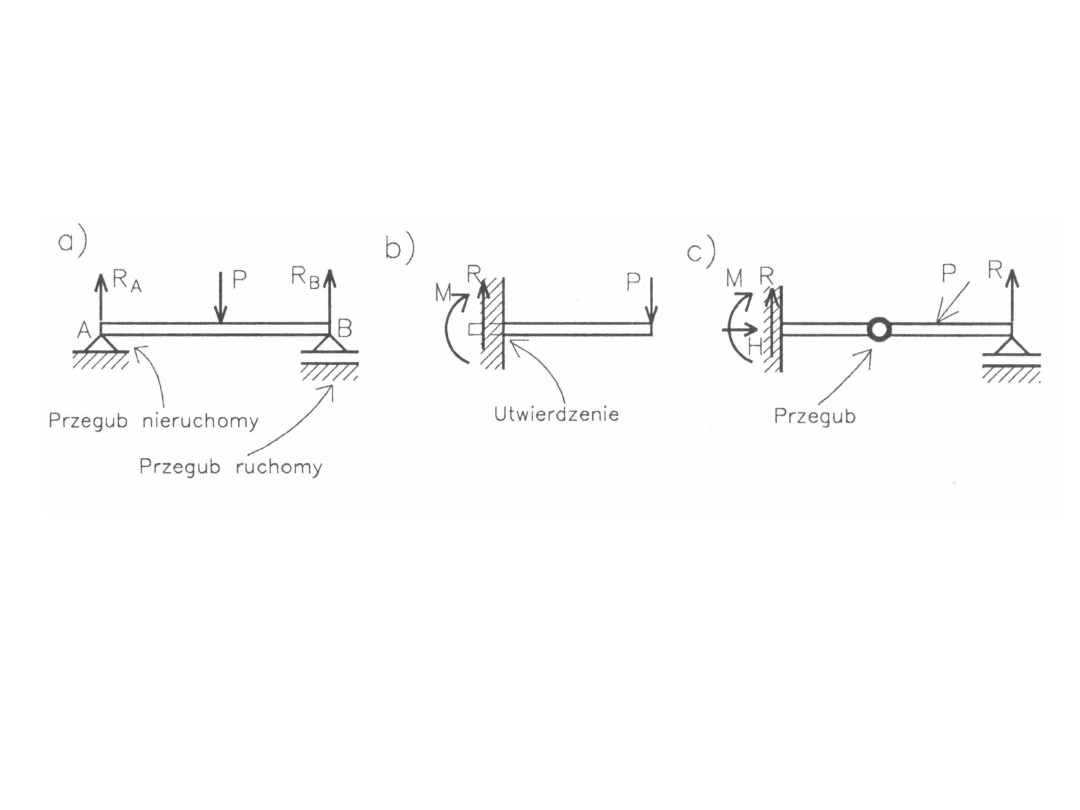
Sposoby podparcia belek

136

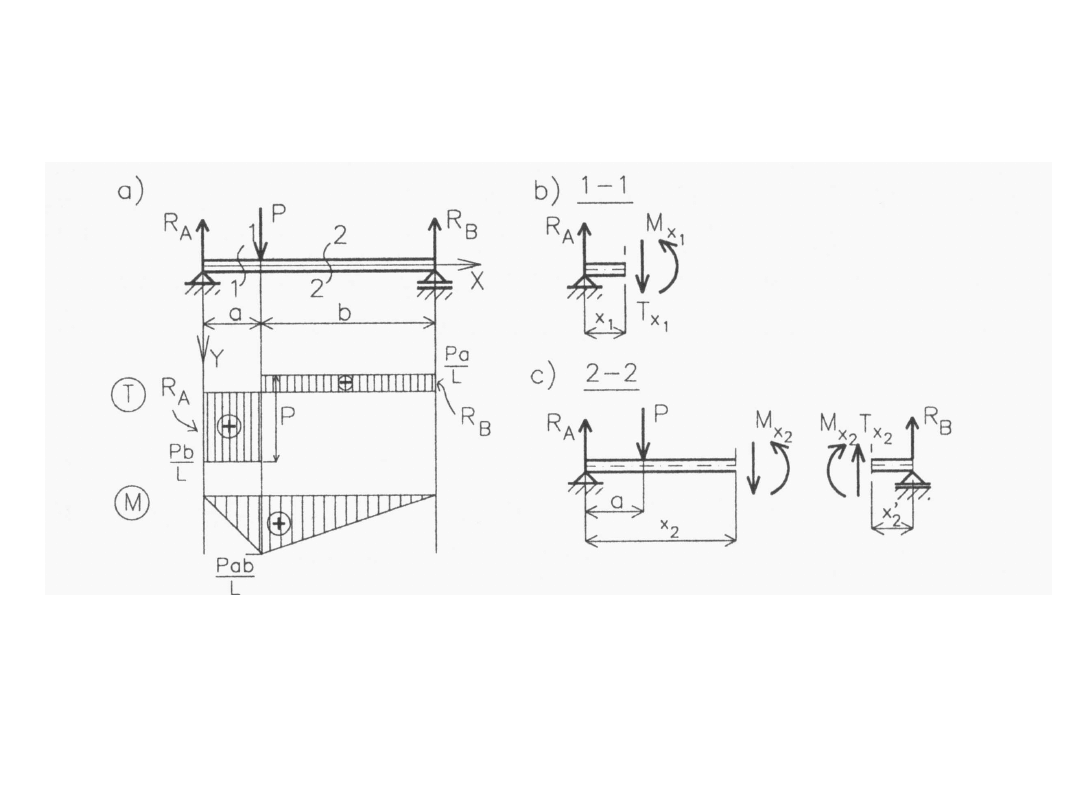
Przykład

137

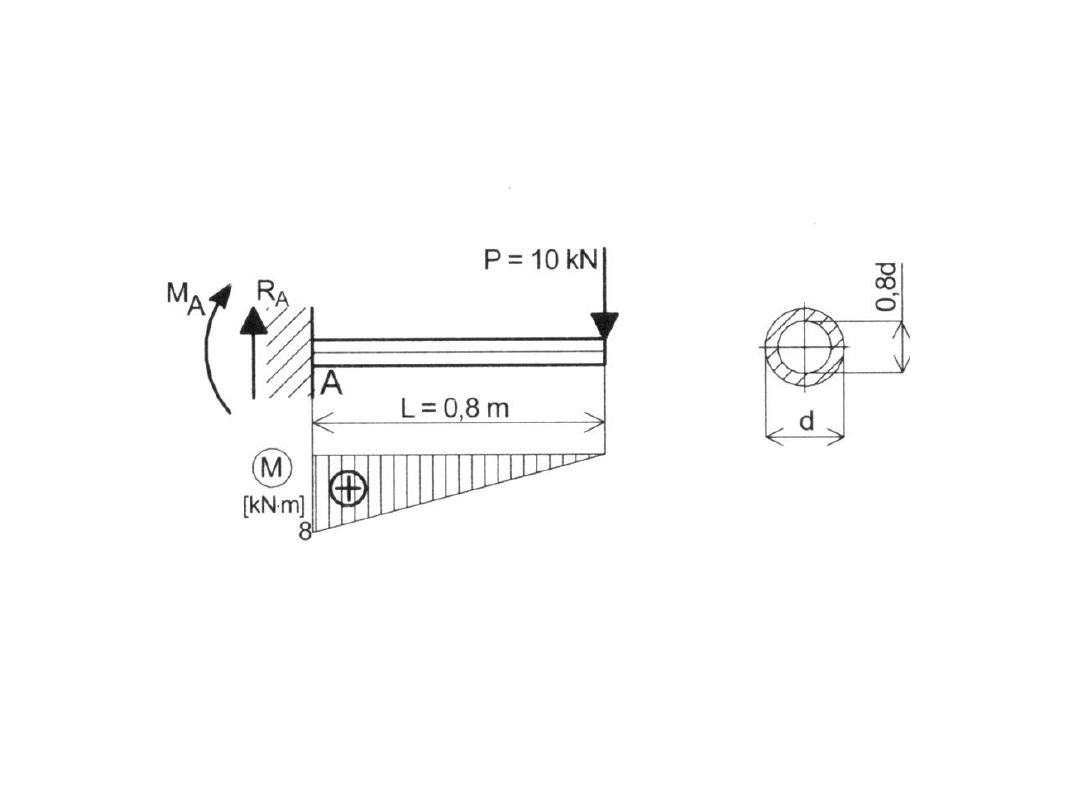
Zadanie