21. Liczba pierwsza:

a) nie może być podzielna przez 7

b) nie może być podzielna przez 8

c) nie może być sumą kwadratów dwóch liczb całkowitych większych od 1

22. Długość jednej z przyprostokątnych w trójkącie prostokątnym jest liczbą całkowitą. Druga przyprostokątna jest od niej dwa razy dłuższa. Długość przeciwprostokątnej w tym trójkącie:

a) jest całkowita b) jest niewymierna c) jest wielokrotnością liczby

23. Układ równań

a) ma rozwiązanie, które na układzie współrzędnych leży wewnątrz koła o środku w punkcie
i promieniu r=3

b) ma dwa rozwiązania

c) ma nieskończenie wiele rozwiązań

24. Liczba 0,(428571)

a) jest większa niż
b) jest większa niż
c) jest większa niż

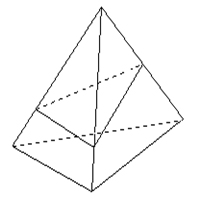
25. Przecięcie czworościanu foremnego i płaszczyzny może być:

a) trójkątem równobocznym

b) kwadratem

c) pięciokątem foremnym

26. Liczba

a) jest większa niż 1 b) jest mniejsza niż 1 c) jest równa 1

27. Które z brył mają oś symetrii ?

a) sześcian b) czworościan foremny c) ostrosłup prawidłowy pięciokątny

28. Suma cyfr liczby dwucyfrowej n jest równa 9, a suma n i liczby powstałej z przestawiania cyfr w n jest równa 99. Wynika stąd, że liczba n:

a) jest parzysta

b) jest podzielna przez 9

c) jest podzielna przez sześcian pewnej liczby naturalnej

29. Który z grafów przedstawia funkcję rosnącą ?

a)
b)
c)

30. Funkcja

a) liczbom wymiernym przypisuje wartości wymienne

b) liczbom niewymiernym przypisuje wartości niewymierne

c) liczbom dodatnim przypisuje wartości dodatnie

Drogi uczestniku!

Przewidziany czas na olimpiadę z matematyki to 65 minut.

Życzymy powodzenia!!!

1. Linia prosta:

a) ma dokładnie jeden środek symetrii

b) ma nieskończenie wiele środków symetrii

c) nie ma środka symetrii

2. Równanie ( 2a + 3 ) x - 7 = ( a - 3 ) x + b

a) ma nieskończenie wiele rozwiązań, gdy a = -6, b = -7

b) ma dokładnie jedno rozwiązanie, gdy a
-6

c) dla pewnych wartości a, b nie ma rozwiązań

3. Liczba

a) jest równa

b) jest równa

c) jest równa

4. Rozwiązanie równania

a) należy do przedziału (0, 2)

b) jest mniejsze niż 5,26

c) jest większe niż

5. Zbiór rozwiązań nierówności
można narysować jako pewną figurę geometryczną w układzie współrzędnych. Pole tej figury jest równe:

a) 16 b) 32 c)

6. Punkt ( 12, 3) należy do wykresu funkcji

zatem a jest równe:

a)
b)
c)

7. Rysunek przedstawia wykres funkcji:

a)

b)

c)

8. Jeśli dla pewnej liczby rzeczywistej x spełniona jest nierówność
to:

a) x>0

b) x należy do zbioru zaznaczonego na osi liczbowej

c) należy do przedziału

9. Funkcja, której wykres jest symetryczny do wykresu funkcji
względem osi OY, to:

a)
b)
c)

10. Kwadrat sumy dwóch liczb parzystych pomniejszony o kwadrat ich różnicy:

a) jest liczbą parzystą b) jest liczbą podzielna przez 4 c) jest liczbą podzielną przez 16

11. Liczbą wymierną może być:

a) suma dwóch liczb niewymiernych

b) różnica dwóch liczb niewymiernych

c) iloczyn dwóch liczb niewymiernych

12. Wykres funkcji

a) ma jeden punkt wspólny z osią OX

b) ma dwa punkty wspólne z osią OX

c) nie ma punktów wspólnych z osią OX

13. Jeśli A jest środkiem okręgu o promieniu
długości
, a C jest środkiem okręgu o
promieniu długości
, to jaka część
kwadratu ABCD jest zakreskowana?

a) ponad 57%

b) ponad 58%

c) ponad 59%

14. Co możemy powiedzieć o wartości parametru a, jeśli zarówno
jak i
jest funkcją rosnącą?

a) a jest dodatnie

b) a należy do zbioru zaznaczonego na osi liczbowej

c) a jest liczbą wymierną

15. Ile nie przecinających się cięciw o długości
można narysować w okręgu o promieniu 1 ?

a) cztery b) pięć c) sześć

16. Tomek wypisał kolejno wszystkie liczby od 1 do 2048. Ile razy napisał cyfrę 3 ?

a) 412 b) 598 c) 615

17. Z szachownicy usunięto po cztery pola
w każdym narożniku. Na ile sposobów
można na pozostałej części szachownicy
ułożyć osiem wież tak, by żadne dwie nie
szachowały się wzajemnie?

a) 40320 b) 576 c) 512

18. Ania, Basia i Czarek nalewają ze stałą prędkością mleko do kubków o trzech rożnych kształtach.

Kubek Ani
Kubek Basi
Kubek Czarka

Jak wyglądają wykresy wysokości h(t) mleka w kubku w zależności od czasu dla każdego z dzieci?

a) Ania
Basia
Czarek

b) Ania
Basia
Czarek

c) Ania
Basia
Czarek

19. Ile razy w rozkładzie na czynniki pierwsze liczby
wystąpi liczba 3?

a) 44 b) 47 c) 48

20. Siedmiokąt foremny:

a) ma 14 przekątnych b) może być wpisany w okrąg c) może być opisany na okręgu

Matematyka 2004

GIMNAZJUM KLASA 2

Matematyka

GIMNAZJUM

KLASA 2

ul. Grochowska 341/ 268

03 - 822 Warszawa

tel. [phone]

fax. [phone]

---