STUDIA PODYPLOMOWE

PRACA KOŃCOWA

Marcin Bińkowski

Modelowanie w matematyce i fizyce z wykorzystaniem programu Excel.

Promotor pracy: ………………………………………

WARSZAWA, 2006 r.

Marcin Bińkowski

Modelowanie w matematyce i fizyce z wykorzystaniem programu Excel.

Rok akademicki 2005/2006

Opiekun specjalności: ……………………………………………………

……………………………………………………

Kwalifikuję do złożenia jako pracę końcową w Wyższej Szkole Informatyki Stosowanej i Zarządzania Ocena pracy ……………………………………………………… ……………………………………………………… Data i podpis promotora

Złożono dnia ……………………………………………………… ……………………………… Podpis Pieczęć Studium

Ocena recenzenta: ………………………………………………… Imię i nazwisko recenzenta: ……………………………………… Dopuszczono do obrony ………………………………………… Data i podpis kierownika

Strona 2 Uwaga: Tę stronę umieścić tylko w pierwszym egzemplarzu pracy.

STUDIA PODYPLOMOWE Rok akademicki …………………

Temat nr:

Karta tematu pracy końcowej

Nr albumu: …………… Imię i nazwisko: ……………………………………………. Specjalność: ………………………………………………… Rok rozpoczęcia studiów: ………………… tryb ……………………………

Tytuł pracy: Modelowanie w matematyce i fizyce z wykorzystaniem programu Excel.

Konspekt: ……………………………… podpis słuchacza

Przewidywany termin ukończenia pracy: ……………………………………

Imię i nazwisko promotora: ………………………………………………….

Akceptuję temat i podejmuję się prowadzenia pracy Zatwierdzam:

……………………………… ………………………………

podpis opiekuna pracy podpis Kierownika Studium

Warszawa, dnia …………………

Spis treści

Wstęp.

Pracę tę podjąłem w przekonaniu, że właściwe wykorzystanie technologii informacyjnej (w dalszej części pracy stosuję skrót TI) może zapewnić moim uczniom wszechstronną samodzielność w odkrywaniu praw fizyki. Analiza możliwości, jakie stwarza oferta rynku TI dla polskiego nauczyciela i podjęcie próby weryfikacji praktycznej opisanych w pracy rozwiązań dydaktycznych przekonuje, że na poziomie gimnazjum możliwe jest wykorzystywanie TI podczas zajęć z uczniami i w pracy uczniów oraz jej stosowanie w dydaktyce fizyki.

Technologia Informacyjna przyczynia się w istotnej mierze do efektywności uczenia się (pozwala optymalnie wykorzystać czas zajęć, upodabnia pracę uczniów do pracy badawczej), oraz przyczynia się do pogłębionego zrozumienia fizyki; uczy wykorzystania komputera i programów narzędziowych w poznawaniu prawidłowości fizycznych.

Moją pracę podzieliłem na dwa główne działy. W rozdziale pierwszym dokonuję analizy wybranych programów komputerowych, które są dostępne dla nauczyciela fizyki pod kątem wykorzystania ich w procesie dydaktycznym. W rozdziale drugim przedstawiam przykłady sposobów wykorzystania TI, prezentując szereg jednostek dydaktycznych z zakresu mechaniki. W rozwiązaniach tych, przy wprowadzaniu nowych dla ucznia praw i definicji, wykorzystuję arkusz kalkulacyjny Maicrosoft .Excel i program komputerowy Modellus.

Wprowadzenie - programy do modelowania („Modelus”, Excel).

W rozdziale tym opiszę, dostępny na rynku program komputerowy Modellus oraz arkusz kalkulacyjny firmy Maicrosoft - Excel, opiszę niektóre ich funkcję i możliwości oraz ocenię ich przydatność w nauczaniu i uczeniu się fizyki, posługując się następującymi kryteriami:

• łatwość obsługi,

• dostępność dla ucznia i nauczyciela.

Program „Modellus”

Autor: prof. Witor Duarte Teodoro, Nowy Uniwersytet, Lizbona.

Polska wersja: J. Dunin - Borkowski, E. Kawecka, G. Kapciak, W. Kranas, OEIiZK.

Program komputerowy Modellus umożliwia budowę i analizę modeli matematycznych oraz opartych na tych modelach symulacji procesów i zjawisk, a także tworzenie powiązanych z nimi animacji. Jest to program otwarty, może być wykorzystywany w nauczaniu przedmiotów przyrodniczych (fizyki, chemii, biologii i geografii), informatyki i technologii informacyjnej na poziomie gimnazjum, liceum profilowanego i technikum. Umożliwia analizę i symulację gotowych modeli (zawartych w dołączonej bibliotece), a także tworzenie nowych, według pomysłu nauczyciela czy ucznia. Daje możliwość nauczania konstruktywistycznego, stosowania szeroko pojętej integracji międzyprzedmiotowej i właściwego wykorzystania technologii informacyjnej w nauczaniu przedmiotowym.

Możemy wykorzystać następujące modele:

Przedmiot - cele edukacyjne - osiągnięcia	Treści nauczania	Tematy (modele) w programie Modellus przyporządkowane do treści nauczania Nazwa pliku - opis modelu
Matematyka Cele edukacyjne: - Budowanie modeli matematycznych dla konkretnych sytuacji.	Dostrzeganie, wykorzystywanie i interpretowanie zależności funkcyjnych; interpretowanie związków wyrażonych za pomocą wzorów, wykresów, schematów, diagramów, tabel.	Wszystkie modele
Fizyka z astronomią Cele edukacyjne: - Poznanie podstawowych praw opisujących przebieg zjawisk fizycznych i astronomicznych w przyrodzie. Osiągnięcia: - Opisywanie zjawisk fizycznych i rozwiązywanie problemów fizycznych i astronomicznych z zastosowaniem modeli i technik matematycznych.	Opis ruchów prostoliniowych. Ruch i siły. Ruch drgający. Oddziaływania grawitacyjne. Loty kosmiczne. Zasada zachowania energii. Zjawisko indukcji elektromagnetycznej. Układ Słoneczny.	marsz.mdl - animacja ilustrująca różnicę między położeniem i drogą lodz.mdl - animacja składania prędkości na przykładzie ruchu łódki rownia.mdl - symulacja zsuwania się klocka z równi przedstawiająca wektory sił (z tarciem i bez tarcia) galileo.mdl - symulacja na tle zdjęć stroboskopowych ruchu wraz z oryginalnym tekstem Galileusza !poznaj.mdl - symulacja rzutu piłki umożliwiająca zmianę prędkości wahadlo.mdl - symulacja drgań wahadła matematycznego pokazująca wektory sił, prędkości i przyśpieszeń oscyl_algor.mdl - numeryczny model oscylatora tłumionego fale_rodzaj.mdl - animacja fal poprzecznych i podłużnych pole_gr.mdl - symulacja reprezentacji pola grawitacyjnego bilard.mdl - gra symulacyjna polegająca na dobraniu takiej prędkości początkowej satelity, aby trafić w cel slalom.mdl - gra symulacyjna polegająca na dobraniu takiej prędkości początkowej satelity, aby przeszedł między dwoma "słupkami" satelita.mdl - zmiany orbity satelity za pomocą silników w celu dobrania jego prędkości orbitalnej en_pion.mdl - przemiany energii przy rzucie pionowym en_spad.mdl - przemiany energii przy spadku swobodnym faraday.mdl - animacja ilustrująca prawo indukcji elekromagnetycznej planety.mdl - animacja ruchu planet w układzie geo- i heliocentrycznym ptol.mdl - animacja ruchu planety po epicyklach według modelu Ptolemeusza
Chemia Cele edukacyjne: - Nabycie umiejętności obserwacji i opisu zjawisk chemicznych zachodzących w otaczającym świecie. Osiągnięcia: - Dostrzeganie przemian chemicznych w otoczeniu oraz czynników wpływających na ich przebieg.	Działanie niektórych substancji na organizm człowieka: leki, trucizny, alkohole, narkotyki, nawozy, środki ochrony roślin	insulina.mdl - model regulacji poziomu insuliny i glukozy w organizmie człowieka
Biologia Osiągnięcia: - Analizowanie struktury i funkcjonowania wybranych ekosystemów. - Analizowanie przyczyn zakłóceń stanu zdrowia człowieka.	Relacje wewnątrz- i międzygatunkowe w przyrodzie. Budowa i funkcjonowanie układów organizmu człowieka (układ hormonalny).	ofiara_drap.mdl - model równowagi ekologicznej (ofiara-drapieznik) insulina.mdl - model regulacji poziomu insuliny i glukozy w organizmie człowieka
Informatyka Osiągnięcia: - Wybieranie, łączenie i celowe stosowanie różnych narzędzi informatycznych do rozwiązywania typowych praktycznych i szkolnych problemów ucznia. - Rozwiązywanie umiarkowanie złożonych problemów przez stosowanie poznanych metod algorytmicznych.	Rozwiązywanie problemów za pomocą programów użytkowych. Zapisywanie algorytmów w postaci procedur, które może wykonać komputer. Przykłady testowania i oceny algorytmów. Modelowanie i symulacja za pomocą komputera. Symulowanie zjawisk o znanych prostych modelach. Modelowanie a symulacja. Przykłady tworzenia prostych modeli.	Wszystkie modele bank.mdl - model wzrostu kapitału oscyl_algor.mdl -numeryczny model oscylatora tłumionego wszystkie modele 01.mdl - model rzutu ukośnego 03.mdl - analityczny model oscylatora harmonicznego

A tak wygląda główny panel programu:

Poniżej pokazuję modele (przykładów), który możemy napisać i wykorzystać na lekcji fizyki Jest nim model fali podłużnej i oscylatora tłumionego.

W oknie modelu możemy wpisywać procedury (równania, definiować zmienne), które program wykona (zinterpretuje).

Program ten jest bardzo prosty w obsłudze, tak więc nie wymagający długiego czasu nauki nawet dla ucznia. Ma prosty intuicyjny interfejs, małe wymagania sprzętowe oraz tani, licencja polskiej wersję językową kosztuje 70 zł, a wersja angielska jest darmowa i dostępną w Internecie.

Polecam ten program dla nauczycieli, którzy chcą wzbogacić swoje środki dydaktyczne i mają możliwość wykorzystania komputera na lekcji (rzutnika multimedialnego).

Procedury, aplikacje w Excelu.

Druga z moich propozycji, jest powszechnie znana, dzięki firmie Maicrosoft, a jest to arkusz kalkulacyjny Excel, sprzedawany przez tą firmie w pakiecie biurowym.

Wymaga on większego czasu na naukę i odkrycie jego możliwości, które możemy wykorzystać na lekcjach matematyki, fizyki czy chemii.

Od samego początku należy rozpatrywać arkusz kalkulacyjny Excel jako zbiór powiązanych wzajemnymi zależnościami obiektów. W grupie ważniejszych elementów - obiektów Excela znajdą się przede wszystkim: skoroszyty, arkusze skoroszytu, zakresy danych, arkusze wykresów i wykresy. Dla zaawansowanych użytkowników niebagatelną rolę odgrywają poza tym okna dialogowe, formularze, makropolecenia i inne elementy, których wymienianie w tym momencie ze wzg. na charakter mojej pracy nie ma większego sensu.

Dla początkującego użytkownika, zasiadającego po raz pierwszy do pracy z Excelem, niewątpliwie najważniejszym elementem jest arkusz skoroszytu.

Wygląd arkusza wraz z menu i paskami narzędzi przedstawia rysunek poniżej.

Największą powierzchnię ekranu zajmuje obszar roboczy arkusza podzielonego na komórki, w których przechowywane mogą być dane, uporządkowane w wierszach i kolumnach. Te z kolei ponumerowane są odpowiednio za pomocą liczb oraz liter alfabetu.

W początkowej fazie korzystania z Excela ważne jest zapoznanie się ze sposobami poruszania się po arkuszu roboczym. Typowy układ menu i pasków narzędzi dla programów firmy Microsoft pozwala na intuicyjną obsługę np. osobom korzystającym już wcześniej z edytora tekstów Word.

Rysunek 1

Adresy komórek arkusza oznaczane są poprzez złożenie indeksu kolumny oraz indeksu wiesza. Komórka na przecięciu pierwszej kolumny i pierwszego wiersza posiada adres A1, w tym samym wierszu, ale w drugiej kolumnie - B1. Podobnie komórka na przecięciu trzeciej kolumny i szóstego wiersza ma adres C6. Przykłady adresów pokazane zostały na rysunku 1.

Oprócz takiego sposobu adresowania stosuje się jeszcze poprzez wpisanie własnej nazwy w miejsce standardowego adresu komórki Pole nazwy, który będzie pełnił tą rolę, ale musimy pamiętać aby nie powtórzyć tej nazwy w całym arkuszu, ponieważ automatycznie umieszczana jest w całym arkuszu.

Wprowadzane dane mogą mieć różnoraką postać - między innymi mogą być liczbą, tekstem, datą, godziną, adresem itp.

W większości przypadków należy po wprowadzeniu danych nadać im określony wygląd tzw. format. Format wyświetlania danych jest parametrem charakteryzującym komórkę i zmienia się go w menu: FORMAT/KOMÓRKI.

Typowymi parametrami są wielkość, rodzaj czcionki oraz styl (np. pogrubienie, kursywa, podkreślenie itp.)

Dla wprowadzonych liczb możliwe jest również określanie ilości miejsc po przecinku, sposobu prezentowania ułamków i liczb ujemnych. Dla dat i godzin będących specyficznymi wartościami liczbowymi, jest również możliwe ustawienie sposobu prezentacji specyficznego dla tego rodzaju danych.

Podczas wprowadzania danych łatwo zauważyć, że Excel stara się rozpoznawać na bieżąco format umieszczanych w komórkach liczb, tekstu, dat. Po wprowadzeniu liczby, daty lub godziny, Excel automatycznie wyrównuje zawartość komórki do prawej strony. Po wprowadzeniu tekstu zawartość komórki zostaje wyrównana do lewej strony. Oczywiście sposób wyrównywania możemy w każdym momencie zmienić poprzez naciśnięcie odpowiedniego narzędzia na pasku

lub wybranie polecenia menu FORMAT/KOMÓRKI.

Częstym błędem popełnianym przez początkujących użytkowników programu, jest traktowanie nagłówków wierszy jako kolumny liczby porządkowej. Po wprowadzeniu nagłówków kolumn łatwo zauważyć, że taka "liczba porządkowa" nie jest poprawna, dlatego należy w razie potrzeby wprowadzić kolumnę i wypełnić liczbami.

Innym rodzajem formatu komórki jest wypełnienie oraz obramowania komórek.

Po wybraniu menu FORMAT/KOMÓRKI należy uaktywnić zakładkę OBRAMOWANIE i zastosować odpowiedni sposób obramowania.

Można również zastosować skróconą metodę używając narzędzi z paska.

Podobnie jak obramowanie ustawia się format wypełnienia, różnicę w tym przypadku stanowi wybór zakładki w menu FORMAT/KOMÓRKI.

Wygląd arkusza i zaawansowanie formatowania zależą od indywidualnych potrzeb. Największą uwagę należy do tego przyłożyć, jeżeli arkusz ma zostać później wydrukowany. Niemniej jednak bardzo często pomija się etap formatu komórki w zakresie obramowania, wypełnienia, ustawienia kolorów. Ma to miejsce szczególnie wtedy, gdy arkusze mają zastosowanie wyłącznie do przechowywania danych.

Zawsze jednak warto odpowiednio ustawić przynajmniej podstawowe parametry wyświetlania danych.

Rozpoczynając rozważania na temat obliczeń w Excelu należy podkreślić, że program ma znacznie rozbudowane możliwości wykonywania obliczeń i stanowi potężne narzędzie w rękach użytkownika, który potrafi je wykorzystać. Podstawę do stosowania obliczeń stanowią tzw. formuły.

Formuła to odpowiednio zapisana operacja z wykorzystaniem danych arkusza, po wykonaniu której w komórce zawierającej formułę pojawi się wynik działania formuły.

W zapisie formuła wyróżnia się pewną cechą. Mianowicie rozpoczyna się znakiem równości. Przykłady formuł znajdują się poniżej:

=10+20 <_______> =30-8 <_______> =20*5

Po wpisaniu tych formuł i zatwierdzeniu klawiszem ENTER, w komórce pojawią się odpowiednio następujące liczby: 30, 22 i 100.

W zapisach formuł można wykorzystywać również adresy komórek, a wtedy do formuły podstawiona zostanie zawartość komórki, której adres został wpisany.

Na w przykładzie na rysunku, w komórce E9 dodatkowo zastosowano nawiasy, natomiast w komórce E11 wykorzystano zapis procentowy.

Kolejnym etapem wtajemniczenia są funkcje, które wklejone w odpowiedni sposób do formuły mogą wykonać nawet bardzo skomplikowane obliczenia z zastosowaniem argumentów zdefiniowanych przez użytkownika.

W wielu zestawieniach często spotyka się miejsce (komórkę), w którym zapisana jest liczba będąca podsumowaniem jakiejś serii danych. Przypadek ten jest na tyle powszechny, że w Excelu istnie specjalny przycisk na pasku narzędzi służący wyłącznie do wklejanie funkcji automatycznego sumowania:

Przycisk funkcji SUMA: →

Przed wywołaniem tej funkcji należy pamiętać o konieczności umieszczenia kursora w komórce, w której ma się pojawić wynik sumowania. Uwaga ta dotyczy również innych funkcji wklejanych i wykorzystywanych w formułach.

Podczas wklejania w komórce widoczna jest tekstowa postać funkcji SUMA(). Znajomość syntaktyki w tym przypadku nie jest wymagana, jednak zaawansowanym użytkowników na pewno się przydaje.

Pozostałe funkcje Excela nie mają wyodrębnionych przycisków za pomocą, których można je wklejać do dokumentu. Zadanie to przejmuje Kreator Funkcji i właśnie ikona wywołująca ten moduł znajduje się na pasku narzędzi:

Przycisk Kreatora Funkcji →

Po zastosowaniu tego narzędzia pojawia się okienko dialogowe, w którym można wybrać odpowiednia funkcję.

Excel posiada ok. 200 wbudowanych funkcji, które używa się stosowanie do zapotrzebowania. Obejmują one podstawowe zagadnienia matematyki, statystyki i logiki, operacje na tekstach i bazach danych. Zapoznawanie się z funkcjami Excela nie polega na "wyuczaniu się" na pamięć kolejnych funkcji. Zwykle zastosowania wymagają od nas stosowania określonej grupy funkcji. Tak więc poznawanie funkcji należy poprzedzić skonkretyzowaniem tego jakie funkcje mogą mieć zastosowanie w tworzonych przez użytkownika aplikacjach w najbliższej przyszłości.

Dodatkowo istnieje możliwość rozbudowywania zbioru funkcji o nowe, definiowane przez użytkownika. Jest to kolejny krok i kolejny stopień zaawansowania w posługiwaniu się omawianym arkuszem kalkulacyjnym.

Kolejnym krokiem w pracy z arkuszem jest tworzenie wykresów. Co prawda w dziedzinie tworzenia wykresów istnieje wiele dobrych narzędzi, być może nawet bardziej wyrafinowanych niż Kreator Wykresów Excela. Jednak obecność tego kreatora w programie arkusza kalkulacyjnego sprawia, że użytkownicy chętnie sięgają po niego, tworząc wykresy z danych pochodzących bezpośrednio z Excela.

Jeśli istnieje zestawienie tabelaryczne na podstawie którego ma być utworzony wykres, wystarczy uruchomić kreator wykresów, klikając odpowiedni przycisk z paska narzędzi, lub wybierając polecenie menu: WSTAW/WYKRES.

Kolejną funkcją która może się przydać użytkownikowi jest Formatowanie warunkowe. Formatowanie warunkowe umożliwia wyróżnianie komórek w zależności od warunków spełnianych przez wartość wyświetlaną w komórce. Komórka spełniająca kryteria może zostać wyróżniona poprzez zmianę formatu czcionki, obramowania i/lub wypełnienia.

Przykład 1.

W zestawieniu sprzedaży za 1-szy kwartał chcemy wyróżnić te pozycje, które są nie mniejsze niż 100.

W pierwszym kroku należy zaznaczyć zakres komórek, które chcemy warunkowo sformatować - w naszym przypadku będzie to zakres B2:D7. Następnie z menu” format” wybieramy „formatowanie warunkowe”. Zostaje otwarte okno kreatora formatowania warunkowego. W jego kolejnych pozycjach zaznaczamy:

„Wartość komórki jest” „większa lub równa” „100”

Następnie naciskamy przycisk „Formatuj” i wybieramy odpowiadające nam formatowanie, np. wypełnienie komórki w kolorze niebieskim. Po zaakceptowaniu przyciskiem „OK” zostaną kolorem niebieskim zaznaczone te komórki, które spełniają określone przez nas kryterium, czyli wyświetlają wartość większą lub równą 100.

Jednocześnie możemy dodać maksymalnie trzy warunki, wiele razy się przekonałem ze to trochę mało, ale o tym na końcu tej części.

Przykład 2.

W przykładzie pierwszym chcemy także, aby kolorem czerwonym zostały wyróżnione te komórki, których wartość jest mniejsza niż 90.

Otwórzmy, ponownie okno kreatora formatowania warunkowego i naciśnijmy przycisk „Dodaj>>”. Podobnie jak poprzednio zaznaczamy lub wpisujemy kolejno

„Wartość komórki jest” „mniejsza” „90”

i po naciśnięciu „Formatuj” wybieramy odpowiedni format.

Jeżeli dodaliśmy dwa pokrywające się kryteria (np. 1-szy warunek „jest większe od 10” i 2-gi  „jest większe od 11”, a liczba znajdująca się w komórce to 15) i zdefiniowaliśmy dla nich dwa różne formaty to zostanie zastosowany pierwszy format.

Usuwanie warunków jest bardzo proste, w oknie kreatora formatowania warunkowego naciskamy przycisk „Usuń...” i zaznaczamy te kryteria, które chcemy usunąć.

Ogromną zaletą formatowania warunkowego, jest fakt, że jest ono „dynamiczne”. Jeżeli wartość komórki zostaje zmieniona Excel od razu sprawdza czy spełnia ona kryterium i odpowiednio zmienia format.

Należy też dodać, że formatowanie warunkowe ma pierwszeństwo przed formatowaniem standardowym. Jeżeli sformatujemy komórkę zarówno w sposób tradycyjny jak i warunkowy, a jej wartość będzie spełniała kryteria to zastosowany zostanie format zgodny z formatowaniem warunkowym.

Prawdziwa magia związana z formatowaniem warunkowym zaczyna się wraz z użyciem formuł jako kryterium i tak naprawdę sprowadza się do umiejętnego posługiwania się nimi.

Przykład 3.

Duże zestawiania tabelaryczne jest łatwiej czytać jeżeli co drugi wiersz jest wyróżniony, np. kolorem. Idealnie do tego nadaje się formatowanie warunkowe.

Posłużymy się tym samym zestawieniem co w poprzednich przykładach.

Zaczynamy oczywiście od zaznaczenia obszaru - w naszym przypadku jest to znowu B2:D7, na którym chcemy wykonać formatowanie i otwarcia okna kreatora. Tym razem zamiast „Wartość komórki jest” wybieramy „Formuła jest”, a obok wpisujemy formułę:

=MOD(WIERSZ();2)=1

i wybieramy odpowiedni format, np. wypełnienie komórki w kolorze jasnym niebieskim.

Jak to działa? Excel sprawdza czy formuła jest prawdziwa, jeżeli tak - zostaje nadany format. Weźmy dla przykładu komórkę B3: reszta (MOD) z podzielenia numeru wiersza (3) przez 2 równa się 1 - czyli warunek jest spełniony i Excel nadał format komórce.

Jak już wcześniej wspomniałem formatowanie warunkowe uaktualniane jest każdorazowo wraz ze zdarzeniem zmieniającym spełnienie warunków. Jeżeli usuniemy lub dodamy wiersz wewnątrz naszej tabeli lub posortujemy jej wiersze, wciąż postanie ona prawidłowo (tzn. co drugi wiersz) sformatowana.

Formatowanie warunkowe możemy wykorzystać do wyróżnienia określonej liczby elementów. Przykład ten pokaże, że komórka spełniające kryterium może się znajdować poza formatowanym obszarem.

Przykład 4.

W komórce B9 będziemy wpisywali liczbę wierszy jakie chcemy by były widoczne.

Zaznaczamy całe nasze zestawienie poza wierszem nagłówka. W oknie kreatora wybieramy „Formuła jest” i wpisujemy następującą formułę:

=WIERSZ()-1>$B$9

jako format wybieramy kolor czcionki biały i brak obramowania komórki.

Myślę, że po przestudiowaniu formuły z przykładu 3 zrozumienie tego przykładu nie powinno sprawiać problemów. Czyż raport w ten sposób przygotowany  nie zrobi wrażenia na dyrekcji?

Kolejny pomysł wykorzystania formatowania warunkowego jaki chcę zaprezentować to wykres... bez wykresu.

Przykład 5.

Chcemy graficznie przedstawić jak kształtowała się wielkość sprzedaży według poszczególnych osób.

Po pierwsze powinniśmy stworzyć pomocniczą kolumnę pokazującą nam wartość sprzedaży poszczególnych osób w odpowiednio mniejszej skali. Ja w tym przykładzie podzieliłem sprzedaż przez 30.

Formuła jaka jest zastosowana do uzyskania formatowania to:

=NR.KOLUMNY()-7<=$G2

(tutaj uwaga! aktywną komórką powinna być komórka H2 - co prawda formatowanie warunkowe nadajemy zakresowi, ale należy pamiętać, że formułę wprowadzamy dla aktywnej komórki, na pozostałe komórki zostanie ona „skopiowana”, z zachowaniem reguł adresowania bezpośredniego/pośredniego),

Jeżeli chcemy by nasz wykres był dwukolorowy to pierwszy warunek musi mieć formułę:

=ORAZ(MOD(WIERSZ();2)=0;NR.KOLUMNY()-7<=$G2)

zaś drugi:

=ORAZ(MOD(WIERSZ();2)=1;NR.KOLUMNY()-7<=$G2).

Ostatnie trzy przykłady wykorzystywały funkcje WIERSZ i NR.KOLUMNY.

Oczywiście można wykorzystać inne funkcje, aby uzyskać ciekawe efekty formatowania warunkowego. W kolejnym przykładzie pokażę, że można wykorzystać funkcje wykonujące obliczenia niejako w tle i na ich podstawie sformatować spełniające kryteria komórki.

Przykład 6.

Chcemy wyróżnić w naszym zestawieniu dwu pracowników o najwyższej całkowitej sprzedaży. Formatowanie przeprowadzimy na zakresie E2:E7, a formuła jakiej użyjemy to:

=E2>=MAX.K($E$2:$E$7;2) przy założeniu, że aktywną komórką jest E2.

Za pomocą formatowania warunkowego można także nieco ulepszyć standardowy raport sum pośrednich. Excel nie formatuje sum generowanych przez kreatora sum pośrednich co sprawie, że raport ten może być nieczytelny. Zaznaczmy cały zakres zajmowany przez raport i jako formułę formatowania warunkowego wpiszmy:

=PRAWY($A1;4)="suma" - oczywiście aktywną komórką jest komórka A1,

i wybierzmy dogodne formatowanie. Teraz, niezależnie od tego jak zmienią się dane zawsze wyróżnione będą wiersze z sumami pośrednimi.

Głównym ograniczeniem formatów warunków jest fakt, że można zastosować maksymalnie trzy warunki, choć w codziennej praktyce zwykle to wystarcza. Ale od czego ludzka pomysłowość? Okazuje się, że i temu zaradzono wykorzystując makra VBA, choć jest to już całkiem inna historia.

Zachęcam do eksperymentowania z formatowaniem warunkowym i formułami -jak widać można uzyskać naprawdę ciekawe efekty i w znacznym stopniu ułatwić i uprzyjemnić sobie pracę.

Teraz opowiem trochę o Funkcji Suma.

Funkcja =SUMA() jest z całą pewnością najczęściej używaną funkcją. Jej składnia to:

=SUMA(liczba1;liczba2;liczba3...).

Oczywiście zwykle sumujemy (podsumowujemy) liczby znajdujące się w kolumnie, w takim przypadku podajemy sumowany zakres zamiast kolejnych liczb, np.:

=SUMA(A1:A10)

Aby wprowadzić funkcję suma możemy oprócz metod standardowych użyć przycisku 'autosumowanie'
z paska standardowego ( w Office XP, przycisk ten został wzbogacony o opcje wstawienia innych funkcji: średnia, licznik, maksimum i minimum.

Drugą, bardzo wygodną dla lubiących używać klawiatury możliwością szybkiego wprowadzenia funkcji suma jest wciśnięcie kombinacji klawiszy 'Alt+=' i zaznaczenie obszaru za pomocą klawiszy ze strzałkami.

Kolejną funkcją, którą często się używa jest Suma.Jeżeli.

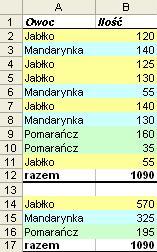
Funkcja =SUMA.JEŻELI() umożliwia zsumowanie wartości spełniających zadane kryteria, tak jak na zdjęciu obok. Formuła w komórce B14 to:

=SUMA.JEŻELI($A$2:$B$11;A14;$B$2:$B$11)

skopiowana została do komórek B15 i B16.

Składnia tej funkcji to:

zakres - zakres zawierający kolumnę z wartościami spełniającymi kryteria

kryteria - sumowane kryterium suma_zakres - sumowane wartości

Jeżeli zakres pokrywa się z suma_zakres ostatnie kryterium możemy pominąć.

Uwagi o funkcjach

Funkcje wstawiamy przez wybranie menu 'wstaw/funkcja', naciśnięcie przycisku 'wstaw funkcję' ze standardowego paska zadań lub przez przycisk 'wstaw funkcję' z paska formuły.

Po wybraniu którejkolwiek z powyższych opcji zostaje otwarte okno kreatora funkcji (zrzut ekranu z wersji XP/2002):

Okno to jest czytelne i nie wymaga opisu. Nowością w Excelu XP/2002 jest bardzo przydatne pole 'wyszukaj funkcję'. Zwracam także uwagę na znajdujący się na dole okna link do pomocy na temat wybranej (zaznaczonej w oknie 'wybierz funkcję') funkcji.

Po wybraniu funkcji otwiera się okno pozwalające nam na wprowadzenie argumentów i wstawienie gotowej funkcji:

Ilość argumentów jest zależna od wybranej funkcji. W przykładzie obok funkcja SUMA.JEŻELI ma trzy argumenty. W polach argumentów wpisujemy zakresy, zaznaczamy zakresy myszą w arkuszu bądź też wpisujemy wartości (stałe). Obok każdego z okien argumentów mamy podgląd jakie wartości przyjmują poszczególne argumenty, zaś poniżej widzimy jaką wartość przyjmuje nasza funkcja.

W sekcji środkowej okna mamy krótki opis funkcji oraz opis argumentu, który aktualnie edytujemy.

Naciśnięcie przycisku 'OK' wstawia gotową funkcję do aktywnej komórki.

Osoby bardziej zaawansowane mogą wpisywać funkcje 'z ręki'. Pomocną opcją w Excelu XP/2002 jest pojawienie się dymku podpowiadającego jakich argumentów wymaga dana funkcja. Przy okazji pojawienie się dymku po wstawieniu otwierającego nawiasu informuje nas o tym, że wstawiliśmy prawidłową nazwę funkcji:

Pasek formularza

Przy pomocy opcji z paska formularzy możemy sterować naszymi zdefiniowanymi zmiennymi. Na pasku formularza znajdują się ikony formantów ActiveX.

W następującej tabeli podano wykaz formantów ActiveX znajdujących się w Przyborniku formantów. Więcej informacji na temat formantów ActiveX można znaleźć w Pomocy języka Visual Basic.

Typy przycisków, pól wyboru i innych formantów z paska narzędzi Formularze

Przyciski, pola wyboru i inne formanty z paska narzędzi Formularze umożliwiają wybór opcji podczas korzystania z formularza. Na przykład, jeśli tworzysz formularz osobowy, możesz dodać dwa przyciski opcji określające, czy pracownik jest zatrudniony w pełnym, czy w niepełnym wymiarze godzin. Ponieważ tylko jeden z przycisków opcji może być zaznaczony, pracownik może być zatrudniony tylko w pełnym albo tylko w niepełnym wymiarze godzin.

Większość z formantów ma właściwości, które mogą być zmieniane. Dla przycisku polecenia i etykiety można zmieniać jedynie właściwości formatowania.

Typ formantu	Opis
Etykieta	Tekst, dodawany do arkusza lub formularza, dostarczający informacji na temat formantu, arkusza lub formularza.
Pole grupy	Ramka i etykieta służąca do grupowania powiązanych formantów, takich jak przyciski opcji lub pola wyboru.
Przycisk	Przycisk po kliknięciu uruchamiający makro.
Pole wyboru	Pole, włączające i wyłączające opcję. Na arkuszu lub w grupie można zaznaczyć więcej niż jedno pole wyboru. Aby uzyskać więcej informacji na temat właściwości pola wyboru, kliknij tutaj
Przycisk opcji	Przycisk zaznaczający jedną opcję z grupy opcji zawartych w polu grupy. W polu grupy można zaznaczyć tylko jeden przycisk opcji. Przycisków opcji używa się w przypadkach, gdy dopuszczalna jest tylko jedna z kilku możliwości. Aby uzyskać więcej informacji na temat właściwości przycisku opcji, kliknij tutaj .
Pole listy	Pole zawierające listę elementów. Aby uzyskać więcej informacji na temat właściwości pola listy, kliknij tutaj .

Pole kombi	Rozwijalne pole listy. Element zaznaczony w polu listy jest wyświetlany w polu tekstowym. Aby uzyskać więcej informacji na temat właściwości pola kombi, kliknij tutaj .
Pasek przewijania	Formant służący do przewijania zakresu wartości poprzez klikanie strzałek przewijania lub przeciąganie pola przewijania. Wartości można przesuwać stronami, klikając pomiędzy polem przewijania a strzałką przewijania. Aby uzyskać więcej informacji na temat właściwości paska przewijania, kliknij tutaj .
Pokrętło	Przycisk ze strzałką w górę i strzałką w dół, który można połączyć z komórką. Aby zwiększyć wartość, kliknij strzałkę w górę; aby zmniejszyć wartość, kliknij strzałkę w dół. Aby uzyskać więcej informacji na temat zmiany właściwości pokrętła, kliknij tutaj .

Właściwości sterujące pasków przewijania i pokręteł paska narzędzi Formularze

Do właściwości sterujących paska przewijania należą:

Właściwość	Opis
Wartość bieżąca	Wartość bieżąca pola przewijania na pasku przewijania, która odpowiada względnemu położeniu pola przewijania na pasku.
Wartość minimalna	Wartość minimalna paska przewijania, która odpowiada położeniu u samej góry pionowego paska lub z lewego końca poziomego paska przewijania.
Wartość maksymalna	Wartość maksymalna paska przewijania, która odpowiada położeniu u samego dołu pionowego paska lub z prawego końca poziomego paska przewijania.
Zmiana przyrostowa	Skok wartości odpowiadający odcinkowi, o jaki przesuwa się pole przewijania przy kliknięciu strzałki na końcu paska.
Zmiana strony	Zmiana strony odpowiadająca odcinkowi, o jaki przesuwa się pole przewijania przy kliknięciu paska pomiędzy nim a jedną ze strzałek przewijania.
Łącze komórki	Łącze komórki zwracającej bieżącą wartość paska przewijania. Liczba ta może być wykorzystywana w formułach do zwracania wyniku na podstawie położenia paska przewijania.

Zmiana, przesuwanie oraz zmiana rozmiaru przycisku, pola wyboru lub innego formantu

Aby zmienić formant, dodany za pomocą paska narzędzi Formularze, należy postępować zgodnie z poniższą procedurą.

1. Kliknij prawym przyciskiem myszy formant, który chcesz zmienić, a następnie z menu podręcznego wybierz polecenie Formatuj obiekt.

2. Aby zmienić właściwości formantu, kliknij kartę Formant. Aby uzyskać informacje na temat właściwości formantu, które można zmieniać, kliknij tutaj .

3. Aby zmienić sposób zmiany rozmiaru lub przesuwania formantu podczas zmiany rozmiaru lub przesuwania znajdujących się pod nim komórek, kliknij kartę Właściwości.

4. Kliknij przycisk OK.

5. Aby przesunąć formant, przeciągnij go w inne położenie. Aby wyrównać położenie formantu z liniami siatki komórek, podczas przeciągania formantu trzymaj wciśnięty klawisz ALT.

6. Aby zmienić rozmiar formantu, przeciągnij jeden z uchwytów zaznaczania. Aby zmienić rozmiar formantu zachowując jego proporcje, podczas przeciągania uchwytów wyboru w narożniku trzymaj wciśnięty klawisz SHIFT.

Przełącz siatkę

Jest to przycisk zmieniający nam wygląd arkusza, „wymazuje” charakterystyczną siatkę pól arkusza i dostajemy białą - gładką powierzchnię, co jest wygodne przy prezentacji naszych wyników.

Komentarz

W polu komentarze, możemy umieścić nasze uwagi, adnotacje lub instrukcje, które może wykorzystać osoba, która korzysta z naszego arkusza.

Dodawanie komentarza do komórki, jest proste i wygląda następująco:

1. Kliknij komórkę, do której chcesz dołączyć komentarz.

2. W menu Wstaw, kliknij polecenie Komentarz.

3. W polu wpisz tekst komentarza.

4. Kiedy zakończysz wpisywanie tekstu, kliknij poza polem komentarza.

Uwaga

Kiedy sortujesz elementy arkusza, komentarze przemieszczają się na nowe pozycje razem z elementami w sortowanych wierszach i kolumnach.

Komentarze w tabelach przestawnych są związane z pozycją komórek, do których zostały wprowadzone, a nie z zawartości komórek. Jeżeli przestawiasz tabelę lub w inny sposób zmieniasz jej układ, komentarze nie są przesuwane.

Pod spodem pokazuję jak wygląda wprowadzony otwarty komentarz w arkuszu, gdy jest on zamknięty (nie widoczne pole komentarza) komórka do której jest on przyczepiony oznaczona jest małym czerwonym trójkątem w prawym górnym rogu.

Ten sam arkusz w dwóch oknach

Niekiedy potrzebujemy widzieć jednocześnie dwa różne arkusze, bądź dwa zakresy tego samego arkusza znajdujące się w jednym skoroszycie. jest to możliwe bez uruchamiania dwukrotnie Excela.

Z menu "okno" wybieramy "nowe okno" - teraz aktywny skoroszyt jest otwarty w dwu oknach, każde z nich jest niezależne i zachowuje się tak samo jak by było normalnym oknem skoroszytu. Jedynie po nazwie w pasku aplikacji bądź w pasku okna skoroszytu podany jest po dwukropku kolejny numer otwartego okna.

Klawisze skrótów

Przydatne, ale nie zawsze stosowane to Klawisze skrótów, jest ich dość dużo a stosuję się najczęściej CTRL+C, CTRL+V, CTRL+X i nie warto się stresować tym, że się wszystkich nie zna lub nie pamięta.

Oto zebrane przez Henryka Tomczyka klawisze skrótów Excela (wyszperane dla Excela 97, po części przetestowane przeze mnie na Excelu 2002). Jeżeli posiadacie wiedzę o innych użytecznych skrótach - możecie je dopisać do poniższej listy.

Czynność w EXCEL	Klawisze skrótu
Anulować edycję zawartości komórki lub paska formuły	ESC
Autofiltr	CTRL+6
Cofnięcie ostatniej czynności	CTRL+Z
Dodać do zaznaczonego obszaru inny zakres komórek	SHIFT + F8
Drukowanie	CTRL+P lub CTRL+SHIFT+F12
Edytować aktywną komórkę i umieścić punkt wstawiania na końcu wiersza	F2
Kopiowanie	CTRL+C lub CTRL+INSERT
Kursywa	CTRL+3 lub CTRL+I
Maksymalizuj  / Przywróć okno	CTRL+F10
Minimalizuj okno	CTRL+F9
Odkrycie kolumny (po zaznacz. obszaru o kol. więcej)	CTRL+SHIFT+0
Odkrycie wiersza (po zaznacz. obszaru o wiersz więcej)	CTRL+SHIFT+9
Odkryć kolumny	CTRL+SHIFT+)
Odkryć wiersze	CTRL+SHIFT+(
Otwiera Edytor Visual Basic	ALT+F11
Otwiera okno "Definiuj nazwy"	CTRL+F3
Otwiera okno "Makro"	ALT+F8
Otwiera okno "Utwórz nazwy" (nazwy z etykiet wierszy lub kolumn)	CTRL+SHIFT+F3
Otwieranie pliku	CTRL+O lub CTRL+F12
po wybraniu dowolnej komórki wewnątrz tablicy wybiera zakres obejmujący całą tablicę	CTRL+ *
Podkreślenie tekstu	CTRL+4 lub CTRL+U
Pogrubianie tekstu	CTRL+2
Pokazanie konspektu	CTRL+8
Powtarzanie poprzedniej czynności	CTRL+Y lub F4
Przechodzenie do strony, sekcji, wiersza itd. (okno Przejdź do)	CTRL+G lub F5
Przechodzenie między skoroszytami.	CTRL+F6
Przejście do następnego arkusza	CTRL+PAGE UP
Przejście do ostatniej komórki w arkuszu	CTRL+END
Przejście do początku dokumentu (pierwszej komórki, którą jest zazwyczaj A1)	CTRL+HOME
Przejście do poprzedniego arkusza	CTRL+PAGE DOWN
Przejść do początku wiersza	HOME
Przejść o jeden znak do góry, w dół, w lewo lub w prawo	Klawisze strzałek
Przejść na krawędź bieżącego zakresu	CTRL+ Klawisze strzałek
Przeliczanie aktywnego arkusza	SHIFT + F9
Przeliczanie wszystkich arkuszy we wszystkich otwartych skoroszytach	F9
Przeliczyć wszystkie arkusze w aktywnym skoroszycie	ALT+CTRL+F9
Przełączyć pomiędzy ukrywaniem obiektów, wyświetlaniem obiektów i wyświetlaniem znaczników pozycji obiektów	CTRL+6
Przerwanie długo trwającej operacji	CTRL+ PAUSE
Przy zaznaczonym obiekcie, zaznaczyć wszystkie obiekty arkusza	CTRL+SHIFT+SPACJA
Przywróć okno	CTRL+F5
Ramka wokół komórki	CTRL+SHIFT+7
Rozpocząć formułę	=
Rozpocząć nowy wiersz w tej samej komórce	ALT+ENTER
Rozszerzyć zaznaczony obszar do komórki w lewym górnym rogu okna	SCROLL LOCK, SHIFT+HOME
Rozszerzyć zaznaczony obszar do komórki w prawym dolnym rogu okna	SCROLL LOCK, SHIFT+END
Rozszerzyć zaznaczony obszar do ostatniej niepustej komórki w tej samej kolumnie lub tym samym wierszu, co aktywna komórka	CTRL+ SHIFT+ klawisz strzałki
Rozszerzyć zaznaczony obszar do ostatniej używanej komórki w arkuszu	CTRL+SHIFT+END
Rozszerzyć zaznaczony obszar do początku arkusza	CTRL+SHIFT+HOME
Rozszerzyć zaznaczony obszar do początku wiersza	HOME + SHIFT
Rozszerzyć zaznaczony obszar o jeden ekran w górę	PAGE UP + SHIFT
Rozszerzyć zaznaczony obszar o jedną komórkę	klawisz strzałki + SHIFT
Rozszerzyć zaznaczony obszar w dół o jeden ekran	PAGE DOWN + SHIFT
Skopiować wartość z komórki nad aktywną komórką do komórki lub paska formuły	CTRL+SHIFT+"
Sprawdzanie pisowni	F7
Uaktywnić hiperłącze	ENTER (w komórce z hiperłączem)
Ukrycie kolumny	CTRL+0 (zero)
Ukrycie wiersza	CTRL+9
Ukrywanie (lub odkrywanie) paska Standartowy	CTRL+7
Usunąć obramowania konturowe	CTRL+SHIFT+_
Usunąć tekst do końca wiersza	CTRL+DELETE
Usunąć znak na lewo od kursora lub usunąć zaznaczony obszar	BACKSPACE
Usunąć znak na prawo od kursora lub usunąć zaznaczony obszar	DELETE
Usunięcie wiersza	CTRL+ -
Utworzenie wykresu wykorzystującego bieżący zakres	ALT+F1 lub F11
Wkleić zdefiniowaną nazwę do formuły	F3
Wklejanie	CTRL+V lub INSERT + SHIFT
Wklejenie funkcji do formuły	SHIFT + F3
Włączyć rozszerzanie zaznaczonego obszaru przy użyciu klawiszy strzałek	F8
Wprowadzanie danych z komórki powyżej	CTRL+' lub CTRL+<
Wprowadzanie danych z komórki z lewej (wypełnia w prawo)	CTRL+R lub CTRL+>
Wprowadzić formułę jako formułę tablicową	CTRL+SHIFT+ENTER
Wstawianie bieżącej daty	CTRL+;
Wstawianie bieżącej godziny	CTRL+:
Wstawianie formuły Autosumowania	ALT+=
Wstawianie hiperłącza	CTRL+K
Wstawianie i edycja komentarza komórki	SHIFT + F2
Wstawianie komórki (wiersz, kolumnę)	CTRL+SHIFT+=
Wstawianie nazwy argumentów i nawiasów dla funkcji, gdy wprowadzisz nazwę funkcji w formule	CTRL+SHIFT+A
Wstawianie nowego arkusza (o nazwie Arkusz1)	SHIFT + F11
Wstawianie nowego arkusza (o nazwie Makro1)	CTRL+F11
Wypełna zaznaczone komórki aktywną pozycją	CTRL+ENTER
Wypełnić w dół	CTRL+D
Wyświetla listę Autowypełnienie	ALT+STRZAŁKA W DÓŁ
Wyświetlanie Palety formuły po wpisaniu nazwy funkcji podczas wprowadzania formuły	CTRL+A
Wyświetlić okno dialogowe Formatuj komórki	CTRL+1
Wyświetlić okno dialogowe Styl	ALT+'
Wytnij	Ctrl+ X lub SHIFT+DELETE
Zakończyć edycję zawartości komórki (i przejść o jedną komórkę w dół w zaznaczonym obszarze -ustawienie domyślne)	ENTER
Zakończyć edycję zawartości komórki i przejść o jedną komórkę do góry w zaznaczonym obszarze	ENTER + SHIFT
Zakończyć edycję zawartości komórki i przejść o jedną komórkę w lewo w zaznaczonym obszarze	SHIFT+TAB
Zakończyć edycję zawartości komórki i przejść o jedną komórkę w prawo w zaznaczonym obszarze	TAB
Zamknięcie  skoroszytu	CTRL+W lub CTRL+F4
Zamyka Excela	ALT+F4
Zapisywanie	CTRL+S
Zastosować format Czasu z godziną i minutami ze wskazaniem A.M. lub P.M.	CTRL+SHIFT+@
Zastosować format Daty z dniem, miesiącem i rokiem	CTRL+SHIFT+#
Zastosować format Liczbowy z dwoma cyframi po przecinku, wyświetlaniem spacji między tysiącami i znakiem minus (-) dla wartości ujemnych	CTRL+SHIFT+!
Zastosować format liczby Ogólny	CTRL+SHIFT+~
Zastosować format tekstowy liczby	' (przed liczbą)
Zastosować formatowanie Procentowe bez liczb po przecinku	CTRL+SHIFT+%
Zastosować formatowanie Walutowe z dwoma cyframi po przecinku (liczby ujemne pojawiają się w nawiasach)	CTRL+SHIFT+$
Zastosować formatowanie Wykładnicze z dwoma miejscami po przecinku	CTRL+SHIFT+^
Zastosować lub usunąć kursywę	CTRL+I
Zastosować lub usunąć podkreślenie	CTRL+U
Zastosować lub usunąć pogrubienie	CTRL+B
Zastosować lub usunąć przekreślenie	CTRL+5
Zastosować obramowanie	CTRL+SHIFT+&
Zaznacza komórki zawierające notatki	CTRL+SHIFT+?
Zaznacza wszystkie komórki, do których odnosi się dana formuła (również pośrednio)	CTRL+SHIFT+{
Zaznacza wszystkie komórki, których formuły zawierają odniesienie do aktywnej komórki (również pośrednio)	CTRL+SHIFT+}
Zaznaczanie wszystkiego (kiedy nie wprowadza się ani nie edytuje formuły)	CTRL+A
Zaznaczyć bieżącą kolumnę	CTRL+SPACJA
Zaznaczyć bieżącą tablicę, t.j. tablicę, do której należy aktywna komórka	CTRL+/
Zaznaczyć bieżący obszar wokół aktywnej komórki (obszar danych otoczony przez puste wiersze i puste kolumny)	CTRL+SHIFT+*
Zaznaczyć bieżący wiersz	SHIFT+SPACJA
Zaznaczyć komórki kolumny, które nie są zgodne z wartością w aktywnej komórce tej kolumny. Trzeba zaznaczyć kolumnę rozpoczynającą się do aktywnej komórki.	CTRL+SHIFT+|
Zaznaczyć komórki wiersza, które nie są zgodne z wartością w aktywnej komórce tego wiersza. Trzeba zaznaczyć wiersz rozpoczynający się do aktywnej komórki.	CTRL+\
Zaznaczyć komórki, do których bezpośr. odwołują się formuły w zazn. obszarze	CTRL+[
Zaznaczyć komórki, których formuły zawierają bezpośrednie odniesienie do aktywnej komórki	CTRL+]
Zaznaczyć tylko aktywną komórkę, gdy jest zaznaczonych wiele komórek	BACKSPACE + SHIFT
Zaznaczyć tylko widoczne komórki w zaznaczonym obszarze	ALT+;
Zaznaczyć wszystkie komórki zawierające komentarze	CTRL+SHIFT+O (litera O)
Zmiana czcionki	CTRL+SHIFT+F
Znajdź (w dół) przy zamkniętym już oknie "Znajdź"	SHIFT + F4
Znajdź (w górę) przy zamkniętym już oknie "Znajdź"	CTRL+SHIFT+F4
Znajdź ciąg	CTRL+F
Znajdź i zamień	CTRL+H

Przykłady wykorzystania aplikacji Excela - modelowanie:

• na lekcjach fizyki

• na lekcjach matematyki

W tym rozdziale chciałbym podąć przykłady praktycznego zastosowania arkusza kalkulacyjnego z wykorzystaniem funkcji, które wcześniej zostały opisane. Skupiłem się przede wszystkim na zadaniach z fizyki, ale nie ma żadnych przeszkód aby wykorzystać nabyte umiejętności (wiedzę) w innych zadaniach z zakresu matematyki lub chemii.

Miałem możliwość przeprowadzenia lekcji fizyki z wykorzystaniem komputera wiele razy i wiem jak zmienia się moje oddziaływanie na uczniów oraz w jaki sposób ułatwia mi on pracę.

Najlepszym tego przykładem są lekcje z Astronomii, gdy omawiamy teorie heliocentryczną i poszczególne planety Układu Słonecznego, gdy mówię o Galaktykach (pokazy i animację multimedialne)

Wykorzystuję komputer również w czasie omawiania - wprowadzania tematów z Mechaniki, gdy robię podsumowanie albo gdy chcę pobudzić ich do dyskusji. W tej ostatniej sytuacji najlepiej jest wykorzystać modele fizyczne, czego przykładem mogą być opisane zadania.

Zadanie 1

Utwórz wykres czasu obiegu satelity po orbicie kołowej w zależności od promienia jego orbity oraz oznacz wielkość orbity geostacjonarnej.

Zadanie 2

Utwórz wykres toru rzutu poprzecznego, na wykresie powinny znajdować się dwa takie tory a wybór z listy parametrów rzutu z listy (wielkość H i v) powinny zmieniać tor.

Zadanie 3

Utwórz wykres toru rzutu ukośnego, na wykresie powinny znajdować się dwa takie tory a wybór z listy parametrów rzutu z listy (wielkość H i v) powinny zmieniać tor.

Zadanie 4 (królik i lis)

Z pewnego punktu na łące zaczął uciekać królik z prędkością v_k = 8 m/s po linii prostej. Znajdujący się w odległości l = 20 m od królika lis rozpoczął bezzwłocznie pogoń z prędkością v_l = 12 m/s. Zakładamy, że ruch obu zwierząt odbywa się po linii prostej. Ułóż równania ruchu, oblicz miejsce i czas schwytania królika przez lisa. Następnie narysuj wykres położenia od czasu dla obydwu zwierząt. Po tym napisz równanie i wykreśl wykres dla sytuacji gdy lis rozpoczął pogoń po czasie t₀ = 2 s od momentu startu królika.

Wersja pierwsza

Lis zaczyna pogoń natychmiast, czas zaczynamy liczyć od chwili startu królika, początek układu współrzędnych w miejscu gdzie stał lis.

Równanie ruchu królika

Równanie ruchu lisa

Zwierzęta spotkają się gdy dla tego samego czasu ich położenia będą identyczne, czyli:

Spotkanie nastąpi w punkcie:

Wersja druga

Lis zaczyna pogoń po dwóch sekundach. Czas zaczynamy liczyć w chwili startu królika, początek układu współrzędnych w miejscu gdzie stał lis.

Równanie ruchu królika

Równanie ruchu lisa

Zwierzęta spotkają się gdy dla tego samego czasu ich położenia będą identyczne, czyli:

Spotkanie nastąpi w punkcie:

Należy wykonać wykres drogi od czasu dla lisa i królika przy różnych prędkościach lisa - 10, 12, 15, 20 m/s.

Zadanie 5 (rzeką czy kanałem?)

Z miasta A do miasta B można dostać się zarówno płynąc rzeką opowiadającą nurt o prędkości v_r = 5 km/h jak i kanałem w którym nie ma prądu. Długość odcinka rzeki i kanału pomiędzy miastami jest taka sama i wynosi l = 20 km. Jak długo będzie trwała podróż holownika z miasta A do miasta B i z powrotem w przypadku gdy płynie on: po 1. Rzeką po 2. Kanałem.

Przedstaw rozwiązanie w zależności prędkości holownika i wykonaj odpowiednie wykresy słupkowe skumulowane dla prędkości v_h = 6, 8, 10, 12 km/h (wykresy liniowe).

Podróż kanałem:

Całkowity czas podróży

Podróż rzeką:

Czas podróży pod prąd

Czas podróży z prądem

Całkowity czas podróży

Widzimy, że dla v_r = 0 wzór przyjmuje postać znaną z wersji 1.

W każdym z przypadków podróż kanałem będzie trwała krócej a to dlatego, że podróż z mniejszą prędkością (pod prąd) wchodzi w większą wagą względną do całkowitego czasu (trwa dłużej). Zadanie można rozbudować dodawać wątek ekonomiczny (model ekonomiczny), kolejno przyjmując np.:

a) koszt paliwa dla statku płynącego z maksymalną prędkością wynosi 50 zł/godz.

b) koszt paliwa dla statku płynącego z minimalną prędkością wynosi 10 zł/godz.

c) koszt pracy dwuosobowej załogi w obu przypadkach 50 zł/godz.

d) koszt amortyzacji silnika dla maksymalnej prędkości wynosi 30 zł/godz.

e) koszt amortyzacji silnika dla minimalnej prędkości wynosi 10 zł/godz.

Można oszacować czy np. nie opłaca się płynąć pod prąd rzeką z maksymalną prędkością zaś w dół rzeki z prędkością minimalną.

Tego rodzaju analiza bez użycia arkusza byłaby niezwykle żmudna. Warto też przećwiczyć w tym kontekście użycie nazw arkusza.

Zadanie 6 (zad. 4 z podręcznika G. Białkowskiego do §32)

Dwa jeziora Mroczno i Kaczno połączone są rzeczkami Spadynią i Leniwą. Spadynia ma długość 10 km, a płynie w niej woda z prędkością 15 km/h. Natomiast Leniwa mierzy 30 km i płynie w niej prąd z prędkością 6 km/h, w tym samym kierunku co w Spadyni. Janek wybiera się na objazd obu jezior i rzek motorówką, która może poruszać się względem wody z prędkością 20 km/h. Jaką trasę ma obrać Janek, aby jego podróż trwała najkrócej?

Przedstaw wyniki na wykresie. Następnie utwórz wykres dla następujących wartości prędkości: 16, 18, 20, 24, 30, 40 km/h.

Można to zadanie rozwinąć do małego modelu ekonomicznego, dodając koszt paliwa, amortyzację silnika (motorówki) czy koszt pracy sternika (załogi).

t_c1 = t_szp + t_lpp

t_c2 = t_spp + t_lzp

Zadanie 7

I wersja

Dwaj przyjaciele wybrali się na wycieczkę rowerową, do miejscowości oddalonej o 40 km. Po dojechaniu na miejsce, okazało się, że jeden rower nie nadaje się do dalszej jazdy i nie można go od ręki naprawić. Następnego dnia rano chłopcy postanowili zostawić zepsuty rower u znajomych i wracać do domu na jednym rowerze, w ten sposób, że będą jechać na zmianę. Ustalili, że jeden przejdzie 20 km, zostawi rower i dalej pójdzie pieszo, a drugi przejdzie pieszo pierwsze 20 km i dalej pojedzie na rowerze. (jedna przesiadka)

II wersja

W drugiej wersji chłopcy przesiadają się dwa razy, po 10 km i 20 km.

Podsumowanie.

Szybki rozwój komputerowych systemów nauczania stanowi dla nauczycieli niemałe wyzwanie. Wymusza na nich wprowadzenie TI do procesu nauczania i uczenia się. Moim celem było ułatwienie nauczycielom znalezienia odpowiedzi na pytanie, w jakim stopniu włączyć komputer do procesu nauczania i uczenia się ucznia?

Większość wychowanków chce się uczyć. Ta naturalna chęć poznania świata musi być jednak prawidłowo stymulowana. Tradycyjna kreda i tablica nie wytrzymują konkurencji z telewizją, video lub grami komputerowymi. Dlatego obowiązkiem nauczyciela jest wprowadzanie do nauczania takich środków, które uatrakcyjniają proces nauczania i prawidłowo stymulują poznawanie środowiska.

Niewątpliwie zastosowanie komputera na lekcjach fizyki realizuje zasadę poglądowości nauczania, ale nie tylko. Niestety, lekcje fizyki nie budzą ostatnio wielkiego zainteresowania wśród uczniów, dlatego staramy się wprowadzać jak najwięcej nowych środków, które przyciągną ich uwagę i wzbudzą zainteresowanie przedmiotem. Komputer jako środek dydaktyczny wyposażony w oprogramowanie sprawdza się tu doskonale. Uatrakcyjnia proces dydaktyczny, zmusza do indywidualnej pracy oraz logicznego i konstruktywnego myślenia.

T właśnie modelowanie komputerowe, czyli tworzenie w języku komputera modelu układu lub zjawiska fizycznego, umożliwia prowadzenie lub prezentację doświadczeń teoretycznych na tym modelu i spełnienie powyższych założeń.

Niektóre programy to jednak także zagrożenia. Łatwość, z jaką można przeprowadzić eksperyment wirtualny, pozbawia go błędów jakie możemy spotkać w rzeczywistości (rachunkowe, ludzkie), jest to zachętą do unikania doświadczeń naturalnych. Przy tym idealizują świat, jak wiemy modele są uproszczoną jego wersją. Wydaje się, że wszystko działa bezbłędnie. Nawet jeżeli istnieje rachunek błędów (rzadko), to bywa on wyidealizowany. Wirtualne pomoce dydaktyczne (np. wspomniany rachunek błędów wykonywany może być automatycznie) przyspieszają proces przyswajania nowych wiadomości, ale po drodze uczeń może zgubić istotne umiejętności np. tworzenie wykresów bez pomocy kreatora, czy analizy błędów. Dlatego rolą nauczyciela jest również mówienie o tych błędach, o uproszczeniach modelu, tak aby uczeń miał pełną wiedzę na temat otaczającego świata.

Z moich doświadczeń, dyskusji z uczniami, wynika że uczniowie zauważają jak bardzo jest skomplikowany (złożony) świat i nasze modele są uproszczone i wyidealizowane.

Bibliografia.

1. http://excel.educom.pl/

2. http://republika.pl/excel/

3. http://phoenix.sce.fct.unl.pt/modellus/

4. http://modellus.oeiizk.waw.pl/metodyka.html.

5. Praca magisterska pt. „Technologia Informacyjna w procesie dydaktycznym fizyki - analiza możliwości wykorzystania i przykłady rozwiązań dydaktycznych na poziomie gimnazjum”, Marcin Bińkowski, Wydział Fizyki i Chemii, Łódź 2002.

Ewa Gurbiel, Grażyna Hardt-Olejniczak, Ewa Kołczyk, Helena Krupicka, Maciej M. Sysło - Komputery, informatyka, komunikacja i technologia informacyjna, Komputer w Szkole nr 1/1998.

wg http://modellus.oeiizk.waw.pl/metodyka.html.

Pasek formularza

Przełącz siatkę

Pasek Przewijania

---