5. RÓWNANIE ILOŚCI RUCHU MASY

Pojęcie ilości ruchu masy strumienia

Ilość ruchu masy jest pojęciem dotyczącym ośrodków ciągłych (płynów) i jest odpowiednikiem pojęcia pędu, które zwykle dotyczy ciał stałych (lub wydzielonych fragmentów strumienia o określonej masie).

Ilością ruchu masy strumienia nazywa się iloczyn jego prędkości i strumienia masy (wydatku masowego):

(5.1)

Ilość ruchu masy jest wielkością wektorową, jej kierunek i zwrot są zgodne z kierunkiem i zwrotem prędkości strumienia. Łatwo wykazać, że ilość ruchu strumienia wyrażą się w jednostkach siły (N).

Równanie ilości ruchu i jego zastosowanie

W obliczeniach gazodynamicznych i wytrzymałościowych silników turbinowych, w tym również maszyn wirnikowych, niezbędne jest wyznaczanie sił oddziaływania strumienia powietrza i spalin na ścianki kanałów przepływowych oraz na łopatki sprężarki i turbiny, w celu wyznaczenia obciążeń mechanicznych tych elementów.

Wiadomo, że każdemu przepływowi strumienia przez kanał towarzyszy zmiana jego parametrów, będąca następstwem gazodynamicznego oddziaływania ścianek kanału (a także ciał znajdujących się w kanale) na strumień. Zgodnie z prawem akcji i reakcji strumień oddziałuje reakcyjnie na ścianki kanału oraz na ciała znajdujące się w kanale, z równą siłą, która jest w ogólnym przypadku wypadko­wą wszystkich sił normalnych (ciśnień) i stycznych (tarcia). W celu określenia tej siły należy znać rozkład ciśnień i prędkości strumienia na powierzchni ścianek opływanych ciał, co nie jest rzeczą prostą nawet w przypadku opływu pojedynczego ciała.

Znacznie łatwiej jest wykorzystać do tego celu zasadę o zmianie ilości ruchu punktów materialnych, którą Euler przystosował dla przepływów ustalonych.

Układając równanie ilości ruchu według Eulera, należy przede wszystkim wyznaczyć powierzchnię kontrolną, obejmującą interesujący nas układ sił, i przyłożyć do niej siły oddziaływania odrzuconej części strumienia, znajdującej się poza powierzchnią kontrolną. Dla przepływu strumienia przez kanały, powierzchnie kontrolną mogą stanowić ścianki kanału i powierzchnie wydzielonych prze­krojów 1-1 oraz 2-2.

Rys. 5.1 Model przepływu dla równania ilości ruchu

W przypadku oddziaływania na strumień sił pochodzących od opływanego profilu, powierzchnię kontrolną umieszcza się w dostatecznej odległości od niego, aby można było uznać ciśnienie na tej powierzchni za stałe i równe ciśnieniu przepływu niezaburzonego.

Dla modelu przepływowego, przedstawionego na rysunku 5.1, wypadkowa układu sił, działającego na strumień wydzielony powierzchnią kontrolną a, b, c, d jest równa, zgodnie z zasadą ilości ruchu według Eulera, przyrostowi ilości ru­chu masy przepływającej przez tę powierzchnię w jednostce czasu.

(5.2)

gdzie:

- ilość ruchu masy wypływającej i dopływającej przez element powierzchni kontrolnej w jednostce czasu;

- wypadkowa układu sił, równa sumie wypadkowej siły ciśnienia na

powierzchnię kontrolną oraz siły oddziaływania profilu na

strumień.

Jeżeli w strumieniu znajduje się nie jeden profil, lecz palisada profilów, to siła będzie wypadkową dla całej palisady. W przypadku, gdy strumień przepływa jedynie przez kanał, będzie to wypadkowa siła oddziaływania ścianek kanału na strumień.

Siła oddziaływania strumienia na ścianki kanału, lub na opływany przez niego profil, będzie równa co do wielkości i przeciwna co do zwrotu:

Dla przepływu jednorodnego i ustalonego równanie (5.2) zapisać można w postaci:

(5.3)

lub w postaci analitycznej (w wielkościach skalarnych) dla przypadku jak na rys. 5.1:

(5.4)

Bardziej prostą postać będzie miało równanie ilości ruchu w wielkościach skalarnych dla osiowo-symetrycznego przepływu strumienia, np. przez dyszę (rys.5.2).

Rys. 5.2 Model przepływu strumienia przez dyszę
(dla równania ilości ruchu masy)

Przyjmując zwrot osi x zgodny z kierunkiem przepływu strumienia, równanie przyjmie postać:

(5.5)

W rzeczywistych warunkach pracy dyszy prawa strona równania jest dodatnia, a zatem na rozpatrywaną dyszę działa od strony strumienia siła osiowa o kierunku zgodnym z kierunkiem przepływu strumienia:

Równanie momentu ilości ruchu i jego zastosowanie

W celu określenia momentów sił, powstających w wyniku przepływu strumieni przez każdy kanał (przede wszystkim znajdujący się w ruchu obrotowym), najprościej jest posłużyć się równaniem momentu ilości ruchu.

Równanie to można otrzymać na podstawie zasady d'Alemberta lub znanej w mechanice zasady o zmianie momentu ilości ruchu układu punktów materialnych. W przypadku zasady o zmianie momentu ilości ruchu, należy rozważyć ruch strumienia gazu, przepływającego w kanale dowolnego kształtu maszyny wirnikowej, przedstawionej na rysunku 5.3 (5.3a - osiowej, 5.3b - promieniowej), obracającej się dookoła osi 0-0 ze stałą prędkością obrotową. Należ przy tym założyć, że środki geometryczne powierzchni dolotowej A₁ w przekroju 1-1 i wylotowej A₂ w przekroju 2-2 tego kanału leżą odpowiednio na promieniach r₁ oraz r₂ od osi obrotu 0-0.

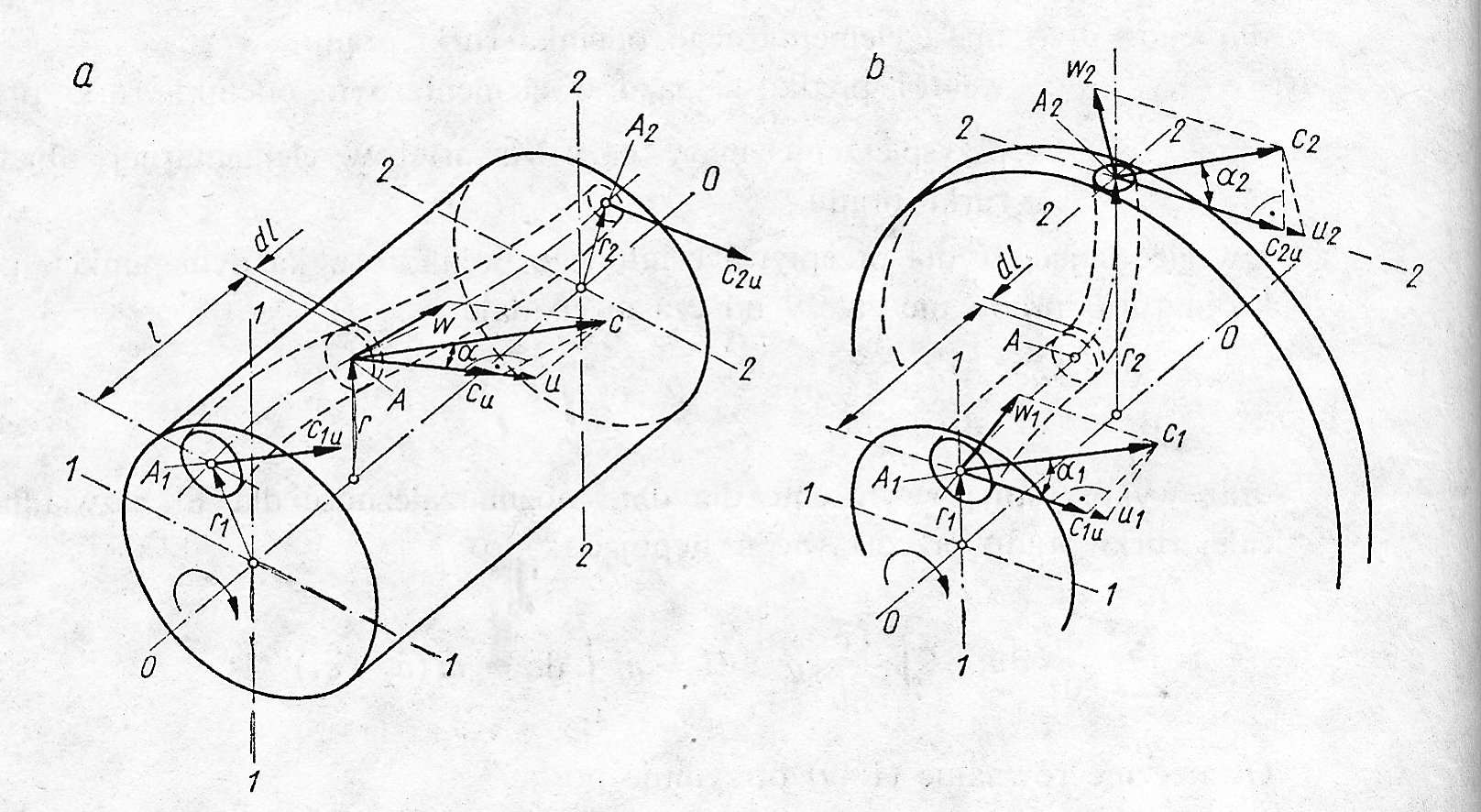
Rys. 5.3 Model przepływu przez kanał maszyny wirnikowej

a - osiowej, b - odśrodkowej (dla równania momentu ilości ruchu)

Podczas przepływu strumienia przez taki kanał występuje ruch złożony, dla którego w dowolnym przekroju kanału prędkości: bezwzględna c, obwodowa (unoszenia) u i względna w powiązane są zależnością:

(5.6)

Rzuty prędkości bezwzględnej na kierunek prędkości obwodowej wynosi:

gdzie α oznacza kąt między wektorami prędkości bezwzględnej i obwodowej (rys. 5.4).

Rys. 5.4 Trójkąt prędkości

c - prędkość bezwzględna, u - prędkość obwodowa, w - prędkość względna

W każdym przekroju kanału, wektor prędkości oraz promień wystawiony do punktu przyłożenia tego wektor, tworzą kąt prosty.

Korzystając z zasady zmienności momentu ilości ruchu w czasie można wykazać, że moment wszystkich sił zewnętrznych działających na rozpa­trywany strumień gazu dla dowolnej osi, jest równy zmianie momentu ilości ru­chu tego strumienia w jednostce czasu, względem tej samej osi.

(5.7)

Momentem sił zewnętrznych w sprężarce jest moment obrotowy jej napędu, po­wodujący zwiększenie momentu ilości ruchu strumienia powietrza w kanałach przepływowych sprężarki. W turbinie moment roboczy, napędzający urządzenia obciążające turbinę, jest uzyskiwany kosztem zmniejszenia momentu ilości ruchu strumienia spalin w kanałach turbiny. W drugim przypadku w za­pisie (5.7) przyrost momentu ilości ruchu będzie ujemny.

Ogólnie można stwierdzić, że przepływowi strumienia gazu przez wirnik muszą towarzyszyć zmiany momentu ilości ruchu, odpowiadające wielkości momentu pobieranego z wału lub oddawanego na wał wirnika. Należy nadmienić, że zmia­na momentu ilości ruchu może nastąpić również bez udziału wirników; mogą to spowodować na przykład różne kierownice, opływane strumieniem gazu. Szczególnie mogą one sprowadzić do zera istniejący moment ilości ruchu, czyli spowodować tak zwane wyprostowanie strumienia.

5

α

c_u=c cosα

u

w

c

---