PODSTAWY EKONOMETRII - ZAOCZNE

Imię i nazwisko: ............................................................ Pkty: ........... Ocena: .........

Zad. 1. W ciągu dziesięciu tygodni firma Alka_Seltzer śledziła wielkość swojej tygodniowej sprzedaży, swoje wydatki na reklamę (w tys. zł) oraz wydatki na pokazy w sklepach (w tys. zł). Na podstawie zebranych informacji oszacowano model, w którym wielkość tygodniowej sprzedaży w badanym okresie (w tys. zł) potraktowano jako zmienną objaśnianą i otrzymano:

SPRZEDAŻ = 50,16 + 1,6 REKLAMA + 2,15 POKAZY

1. Liczba 50,16 w tym równaniu informuje, że przy zerowych wydatkach na reklamę i na pokazy, sprzedaż kształtowałaby się na poziomie 50,15 tys zł.

2. Liczba 2,15 w tym równaniu informuje, że zmiana o jedną jednostkę wydatków na pokazy (ceteris paribus) skutkuje wzrostem sprzedaży o 2,15 tys zł.

3. Wiedząc, że OSK = 656,1 oraz SKR = 130,53 oceń dobroć dopasowania modelu do obserwacji

R²= 1-(130,53/656,1)=80,1%

model jest źle dopasowany

4. Oceń wpływ czynników losowych na kształtowanie sprzedaży produktów firmy, wiedząc, że przeciętny poziom sprzedaży w badanym okresie wyniósł 74,5 tys. zł.

V= s/ y śr = 4,32/ 74,5 = 5,80 % czynniki losowe mają nieznaczny wpływ na kszt





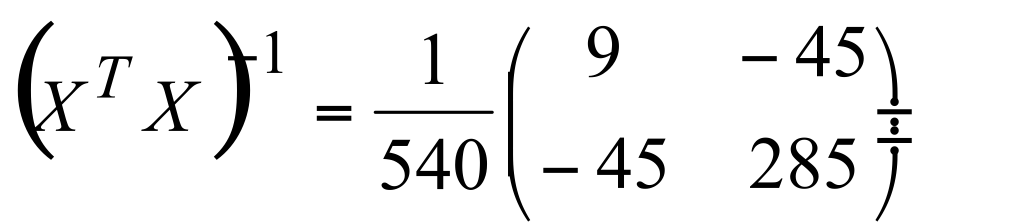
ałtowanie sprzedaźy

s= pierwiastek (130,53/7) = 4,32

Zad. 2. W przedsiębiorstwie postanowiono skonstruować model

opisujący zależność całkowitego kosztu produkcji pewnego wyrobu (Y w tys. zł) od skali produkcji (X w tys. sztuk). Na podstawie zebranych obserwacji otrzymano następujący model:

1. Na podstawie współczynnika kierunkowego tego modelu stwierdzić można wzrost skali produkcji o 1 jednostkę (tys. szt.) powoduje wzrost kosztu produkcji tego wyrobu o 2 tys. zł.

2. Wiedząc, że

ustal szacunkowy błąd średni parametru β₂ mierzącego wpływ skali produkcji na jej koszt

s*pierw c = 1* pierw (6/329) = 0,018

3. Wiedząc, że t_τα = 2,306 sprawdź, czy całkowity koszt produkcji wyrobu zależy od skali produkcji

t= b/d

t= 2/0,018 = 111,11 całkowity koszt produkcji zaleźy od skali produkcji, bo t jest mniejsze od t krytycznego

Zad. 3. Poniższy model opisuje kształtowanie się liczby ciągników w pewnym województwie (Y w tys. sztuk) w latach 1997 - 2005 (t = 1, 2, ...):

Dla modelu tego

1. Liczba 1,2 w tym modelu informuje, że z roku na rok produkcja ciągników rośnie o 1,2 tys szt.

2. Ustal prognozę liczby ciągników w tym województwie na rok 2007 16,4 tys szt..

2007= 11 Y= 1,2*11 +3,2 = 16,4 tys szt

3. Błąd ex ante postawionej prognozy liczby ciągników wynosi 3,0155 .

Obliczenia:

m= s* pierw (1 + xT* (XTX)-1 * x) = 2,3 * pierw (1 + [ 11 1] [0.0167 -0,0833] * [11] = 2,3 *pierw (1,7189) = 3,0155

-0,0833 0,5278 1

4. Postawiona prognoza jest dopuszczalna/ niedopuszczalna, ponieważ

mp = m/Y = 3,0155/16,4 = 18,39%

Zad. 4. Postanowiono skonstruować model wykładniczy

opisujący zmiany wydatków pewnej rodziny na kulturę w kolejnych latach (t = 1, 2,... ). Zebrano odpowiednie obserwacje i oszacowano parametry pomocniczego modelu liniowego otrzymując równanie:

W = 2 + 0.025t

1. Przedstaw sposób utworzenia pomocniczego modelu liniowego

lnY = lnA + Bt lne

lnY = W; lne = 1; lnA =z= e `do' c0

W = z + Bt

2. Model oryginalny po oszacowaniu ma postać: Y = e²* e `do' 0,025 t

Y= 7,39 * e `do' 0,025 t

3. Wykres oszacowanego modelu wykładniczego przedstawia się następująco:

3. Liczba 0.025 informuje, że wydatki wzrastają z roku na rok o 2,5%. Jest to stała stopa wzrostu.

Zad. 5. Postawiono hipotezę, że wartość miesięcznej sprzedaży (Y - w tys. zł) w pewnym sklepie zależy o liczby zatrudnionych sprzedawców (X). Przyjęto, że zależność tę opisuje model potęgowy

.

1. Przedstaw sposób utworzenia pomocniczego modelu liniowego

lnY= ln B0 + ln x `do' B1

lnY= ln B0 + B1 ln x

W = B0 + B1 z

lnY= W; ln B0 = B0; ln x = z

2. Zebrano odpowiednie obserwacje i oszacowano parametry pomocniczego modelu liniowego otrzymując równanie: W = 1,5 + 0.40 Z

Odtwórz postać modelu potęgowego po oszacowaniu:

W= e `do' 1,5 * x `do' 0,40

Y = 4,48 x `do' 0,40

3. Naszkicuj oszacowany model

4. O ile zmieni się sprzedaż, gdy zatrudnienie spadnie o 5%? 0,40 * -5 = -2% sprzedaź spadnie o 2%

9 lutego 2008

9 lutego 2008

A

---