Obliczenia konstrukcyjne i sprawdzające

1. Obliczenie siły P dociskającej tarczę sprzęgła.

Maksymalny moment, jaki może przenosić sprzęgło przeciążeniowe cierne płaskie (Rys. 1) wynosi:

Rys.1 Schemat sprzęgła przeciążeniowego ciernego.

Stąd siła docisku sprężyny wynosi:

2. Obliczenia sprężyny sprzęgła przeciążeniowego.

Obliczenia sprężyny dokonano na podstawie „Podstawy konstrukcji urządzeń precyzyjnych” (9.3.2 Sprężyny naciskowe).

Dane jest obciążenie (obliczone w pkt.1): P=10,95[N].

Rys.2 Sprężyna naciskowa i jej charakterystyka.

Kolejność obliczeń	Zależność do obliczeń	Wartość liczbowa
1. Założenie wskaźnika sprężyny w	zaleca się	w=13 (założono ze względu na kryteria geometryczne)
2. Obliczenie współczynnika poprawkowego k lub wyznaczenie z wykresu		k=1,1017865
3. Przyjęcie naprężenia stycznego τk z uwzględnieniem współczynnika k	α=0,3 - przypadek dynamiczny (dla sprężyn klasy I o trwałości nie mniejszej niż 5·10^6cykli pracy do uszkodzenia) α=0,5 - przypadek statyczny (dla sprężyn klasy II o trwałości nie mniejszej niż 10^5cykli pracy do uszkodzenia sprężyny)	Dla drutu rodzaju C (o dużej wytrzymałości) i klasy I o średnicy 1mm średnia wartość wytrzymałości na rozciąganie wynosi (na podstawie tab. 1): Rm(1mm)=2390[MPa] Przyjęto:
4. Obliczenie średnicy drutu d		Zaokrąglono w górę do zalecanej średnicy drutu i ze względu na kryteria geometryczne przyjęto (na podstawie tab.2): d=1[mm]
5. Obliczenie średnicy sprężyny D
6. Założenie dowolnej liczby zwojów czynnych zc	-	zc=3

7. Obliczenie strzałki ugięcia fn	Wartości współczynnika sprężystości poprzecznej stali zawarte są w przedziale G=7,65·10^4÷ 8,24·10^4[MPa]. Przyjmuje się zwykle G=8·10^4[MPa].
8. Przyjęcie liczby zwojów nieczynnych zn	zn=1,5 - dla sprężyn o zwojach końcowych przyłożonych i szlifowanych lub nieszlifowanych o średnicy drutu d<0,5mm zn=2 - dla sprężyn o zwojach końcowych przyłożonych i szlifowanych lub nieszlifowanych o średnicy drutu d≥0,5mm	(dla sprężyny o zwojach końcowych przyłożonych i szlifowanych o średnicy drutu d=1[mm])
9. Obliczenie całkowitej liczby zwojów
10. Obliczenie sumy prześwitów międzyzwojowych		x=0,37 (współczynnik odczytany z wykresu na rys. 3 )
11. Przyjęcie rodzaju zakończenia sprężyny i obliczenie długość zblokowanej sprężyny lbl	- dla sprężyn o zwojach przyłożonych i szlifowanych - dla sprężyn o zwojach przyłożonych i nieoszlifowanych, gdy z jest liczbą połówkową - dla sprężyn o zwojach przyłożonych i nieoszlifowanych, gdy z jest liczbą całkowitą	(sprężyna o zwojach przyłożonych i szlifowanych)
12. Obliczenie długości ln
13. Obliczenie długości l0
14. Obliczenie wskaźnika smukłości λ
15. Obliczenie wskaźnika sprężystości sprężyny η
16. Sprawdzenie, czy sprężyna ulegnie wyboczeniu	(na podstawie przebiegu graficznego zależności η=f(λ) z rys. 4)	Punkt o współrzędnych (λ, η)=(1,025; 54,16) leży poniżej krzywych, więc sprężyna nie ulegnie wyboczeniu.
Oznaczenia:	w - wskaźnik sprężyny; D - średnica podziałowa sprężyny; d - średnica drutu; k - współczynnik poprawkowy; τk - naprężenia styczne z uwzględnieniem współczynnika k; ks - naprężenia skręcające; G - współczynnik sprężystości poprzecznej materiału sprężyny; fn -strzałka ugięcia; zn - liczna zwojów nieczynnych; zc - liczba zwojów czynnych; z - całkowita liczba zwojów; lbl - długość zblokowanej sprężyny; λ - wskaźnik smukłości; η - wskaźnik sprężystości sprężyny

Rys. 3 Wartość współczynnika x w funkcji wskaźnika sprężyny w dla sprężyn naciskowych.

Rys. 4 Wartości wskaźnika sprężystości sprężyny η w funkcji wskaźnika smukłości λ.

Tab.1 Wytrzymałość na rozciąganie drutu C I.

Tab. 2 Średnice produkowanych drutów sprężynowych.

3. Dobór i sprawdzenie trwałości łożysk tocznych.

Rys. 5 Schemat obciążeń popychacza i nakrętki.

1. wyznaczenie reakcji w łożyskach

Wartość siły P_m wyznaczono na podstawie zależności (rys. 6):

Reakcje w łożyskach (rys. 5) wynoszą:

b) parametry zastosowanych łożysk

Wybrano łożyska firmy Koyo o numerze katalogowym: 607 ZZ.

Rys. 7 Fragment katalogu łożysk tocznych firmy Koyo.

Ze względu na średnicę śruby (4mm) wybrano łożyska o średnicy wewnętrznej równej 7mm. O wyborze łożyska o średnicy zewnętrznej 19mm zdecydowała nośność (rys. 7), będąca większą od nośności łożyska 687 i gabaryty mniejsze w porównaniu do łożyska 627 (spośród trzech możliwych łożysk o średnicy 7mm). Ponieważ łożyska będą znajdować się w mechanizmie obudowanym nie ma potrzeby stosowania łożyska 2SR - zastosowano typ ZZ ze względu na cenę.

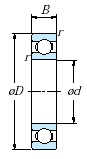
Oznaczenie	Średnica wewnętrzna d[mm]	Średnica zewnętrzna D[mm]	Szerokość B[mm]	Nośność ruchowa Cr[kN]	Nośność spoczynkowa C0[kN]
607	7	19	6	2,60	1,05

c) wyznaczenie trwałości łożysk

Istnieje ścisła zależność między trwałością, nośnością ruchową a obciążeniem zewnętrznym łożysk tocznych, która wyraża się wzorem:

Obciążenie zastępcze wynosi:

• dla łożyska ustalającego:

, czemu odpowiada (odczytana z wykresu na rys. ) wartość e=0,29

Prawdziwa jest zatem nierówność:

Na podstawie powyższej nierówności i wykresu na rys. odczytano wartości współczynników X i Y:

X=0,56

Y=1,50

Zatem obciążenie zastępcze wynosi:

Zaś trwałość:

[mln obrotów]

• dla łożyska ustalanego:

Obciążenie zastępcze wynosi:

P=R_Ay=5,58[N]

Zaś trwałość:

[mln obrotów]

[mln h]

4. Obliczenia kół zębatych.

a) Obliczenia pary kół zębatych

• Przyjęto liczbę zębów
  oraz
  .

• Graniczna liczba zębów z_g, ze względu na uniknięcie podcięcia stopy zęba, dla tego zarysu odniesienia wynosi
  .

• Liczba zębów, ze względu na zaostrzenie wierzchołka wynosi (dla zarysu bez konstrukcyjnego luzu obwodowego):

Ponieważ zachodzą nierówności:

z₁<z_g

z₁+z₂>2z_g

tzn. liczba zębów jednego z kół zębatych jest mniejsza niż graniczna oraz suma zębów jest

wystarczająco duża, konieczne jest zastosowanie korekcji typu P-O, której cechą jest zachowanie zerowej odległości osi kół a_0.

Współczynnik przesunięcia zarysu wynosi:

Dla zębnika:
Średnica podziałowa
Średnica zasadnicza
Średnica wierzchołków
Średnica stóp
Dla koła zębatego:
Średnica podziałowa
Średnica zasadnicza
Średnica wierzchołków
Średnica stóp

b) Obliczenia wytrzymałościowe kół zębatych.

• 
  Wstępne obliczenie minimalnego modułu koła:

Wartości współczynnika kształtu zęba zębnika oraz koła zębatego odczytano na podstawie wykresu z rys. 8:

- dla zębnika;

- dla koła zębatego;

Rys. 8 Wartości kształtu zęba dla kół o uzębieniu zewnętrznym (źródło L. Müller, „Przekładnie zębate. Obliczenia wytrzymałościowe”)

k_g - dopuszczalne naprężenia zginające wynoszą:

, gdzie z_gi odczytujemy z tabeli:

Materiał	25, A11, St3	MO59, MO63
zgi [MPa]	250	100

- dla A11;

- dla MO59;

Obliczono moduł dla zębnika:

;

Obliczono moduł dla koła zębatego:

Wynika stąd wniosek, iż przyjęty moduł m = 0,8 zapewnia nie przekroczenie dopuszczalnych naprężeń zginających.

• Sprawdzenie naprężeń zginających u podstawy zęba.

,

Siła międzyzębna w przypadku zębnika wynosi:

,

zaś w przypadku koła zębatego:

;

Natomiast wskaźnik zazębienia
wyznacza się z zależności:

=0,64 ;

Następnie dokonujemy kolejnych obliczeń dla zębnika a następnie koła zębatego:

;

;

Wyliczamy współczynnik wielkości zęba:

Dla zębnika:

Dla koła zębatego:

Sprawdzamy zatem warunek wytrzymałości sformułowany na początku:

Warunek wytrzymałościowy jak widać jest spełniony.

• Sprawdzenie nacisków powierzchniowych (wg Hertza).

Maksymalne naprężenia ściskające możemy obliczyć z zależności:

,

Podstawiając wartości do wzoru otrzymujemy:

Następnie obliczamy P_obl dla zębnika, będącego kołem czynnym:

Ostatecznie obliczamy maksymalne naprężenia ściskające:

;

MPa

Warunek wytrzymałościowy jest zatem spełniony.

4

P - siła docisku sprężyny

M_sp - moment przenoszony przez sprzęgło; M_sp = 98,55[mNm] (obliczony w punkcie 5 obliczeń konstrukcyjnych)

μ - współczynnik tarcia na powierzchniach ciernych; μ=0,3 (dla pary stal-mosiądz)

i - liczba powierzchni trących

D_s - średnia średnica powierzchni ciernych

D₁ = 27[mm]- średnica wewnętrzna tarczy sprzęgłowej

D₂ = 33[mm] - średnica zewnętrzna tarczy sprzęgłowej

P_m

R_Bx

y

R_Ay

R_By

a

b

x

Q

P_m - siła międzyzębna (działająca wzdłuż linii przyporu)

R_By, R_Bx - reakcje w łożysku ustalającym

R_Ay - reakcje w łożysku ustalanym

Q=100[N] - siła wzdłużna od obciążenia zadanego w temacie

a=16[mm] - odległość między środkiem koła zębatego a środkiem pierwszego łożyska (ustalającego)

b=17[mm] - odległość między środkami łożysk

Oznaczenia:

- moduły Younga materiałów kół,

(stal, dla zębnika);

(mosiądz, dla koła zębatego);

- kąt przyporu;

- szerokość wieńca zębatego,

- średnica podziałowa koła czynnego;

- przełożenie,

- dopuszczalne naciski powierzchniowe (dla koła czynnego wykonanego z A11 )

Oznaczenia:

- siła międzyzębna;

d - średnica podziałowa obliczona w podpunkcie a) (dla zębnika d₁=8mm, dla koła zębatego d₂=38,2mm)

(gdzie ε - wskaźnik zazębienia)

- współczynnik kształtu zęba;

- współczynnik przeciążenia;

- współczynnik nadwyżek dynamicznych;

- współczynnik nierównomiernego rozkładu obciążenia na szerokości zęba;

- współczynnik wielkości zęba;

- szerokość wieńca zębatego;

- współczynnik bezpieczeństwa;

- współczynnik stanu powierzchni;

- współczynnik karbu u podstawy zęba;

M_k - moment obciążający koło zębate

M_z - moment obciążający zębnik

q - współczynnik kształtu zęba

b - szerokość wieńca zębatego

k_g - dopuszczalne naprężenia zginające

ψ- współczynnik szerokości wieńca zębatego

Stopień sprzęgający: i_sp=4,9 (wyznaczony w punkcie 4 obliczeń konstrukcyjnych );

Materiał zębnika: stal A11;

Materiał koła zębatego: MO59;

Współczynnik wysokości głowy zęba: y=1;

Współczynnik wysokości stopy zęba: u=1,4

Moduł uzębienia: m=0,6 (założony)

Kąt zarysu: α=20°

Liczba zębów zębnika: z₁=10

Liczba zębów koła zębatego: z₂=49

L_h - trwałość [h]

n_nut=85,7[obr/min] - prędkość obrotowa nakrętki (obliczona w części pierwszej obliczeń konstrukcyjnych w pkt 3.a)

P_p=R_By=7,38[N] - składowa poprzeczna obciążenia

P_w=R_Bx=100[N] - składowa wzdłużna obciążenia

e - wielkość charakteryzująca zdolność łożyska do przenoszenia obciążeń

P - obciążenie zastępcze

X - współczynnik obciążenia poprzecznego

Y - współczynnik obciążenia wzdłużnego

P_p - składowa poprzeczna obciążenia

P_w - składowa wzdłużna obciążenia

L - trwałość [mln obrotów]

C - nośność ruchowa

P - obciążenie zastępcze

p - wykładnik potęgi wynoszący dla łożysk kulkowych 3

P_m - siła międzyzębna (działająca wzdłuż linii przyporu)

M_nut=65,7 [mNm] - moment potrzebny do obrotu nakrętki

r₁=0,5·d_b2=0,5·36,84=18,42[mm] - promień zasadniczy koła zębatego

α=20^o - kąt przyporu równy kątowi zarysu przy nominalnym rozstawieniu

---