Skompilowane wszystkie odpowiedzi (poza 8, 10, 12, 24, 30 chyba jest niekompletne też) Wersja BIG ze zdjęciami. Jeśli ktoś jest łaskaw i chętny do przepisania zdjęć do pliku to byłoby super jeśli by to potem wrzucił.

   1. Narysować  wykres rozciągania dla stali niskowęglowej i zdefiniować granice wytrzymałości
   2. Narysować wykres rozciągania bez wyraźnej granicy plastyczności i wyjaśnić jak określa się umowna granicę plastyczności
   3. Prawo Hooke'a dla jednoosiowego rozciągania.
   4. Prawo Hooke'a dla ścinania.
   5. Co rozumiemy pod pojęciem naprężenia dopuszczalnego i jak je określamy?
   6. Na czym polega zasada superpozycji, kiedy ja można stosować, a kiedy nie można
   7. Co rozumiemy pod pojęciem układu statycznie niewyznaczalnego i co jest potrzebne do wyznaczania sił i reakcji w takim układzie?
   8. Wyprowadzić wzór na naprężenia obwodowe w pierścieniu poddanym działaniu ciśnienia wewnętrznego.
   9. Co rozumiemy pod pojęciem energii potencjalnej odkształcenia sprężystego i jak  ją obliczamy?
  10. Określić rozkład i znaki naprężeń występujących w jednokierunkowym stanie napięcia, na płaszczyznach nachylonych pod kątami alfa, alfa plus dziewięćdziesiąt stopni oraz alfa plus 270 stopni.
  11. Podać wzory na naprężenia normalne i styczne dla dwuosiowego (płaskiego) stanu naprężenia
  12. Określić zasady konstruowania koła Mohra  dla płaskiego stanu naprężenia (dane s1 i s2).
  13. Narysować rozkład naprężeń i koło Mohra dla płaskiego stanu naprężenia.
  14. Dane są naprężenia sx i sy oraz t. Zastosować koło Mohra w celu wyznaczenia naprężeń głównych  s1 i s2.
  15. Co rozumiemy pod pojęciem liczby Poissona?
  16. Jak określamy odkształcenia w płaskim stanie napięcia
  17. Podać prawo Hooke'a dla dwukierunkowego stanu napięcia
  18. Uogólnione prawo Hooke'a (czego dotyczy i jakimi wzorami się wyraża)
  19. Co rozumiemy pod pojęciem czystego ścinania? Jak wygląda koło Mohra dla czystego ścinania?
  20. Określić zależność pomiędzy modułami sprężystości E i G.
  21. Na czym polegają uproszczone obliczenia na ścinanie?
  22. Na czym polega obliczanie wytrzymałości wału pełnego?
  23. Co rozumiemy pod pojęciem momentu bezwładności figury płaskiej?
  24. Koło Mohra dla momentów bezwładności.
  25. Podać definicje sił normalnych, sił tnących i momentów gnących
  26. Co rozumiemy pod pojęciem belki o równomiernej wytrzymałości na zginanie?
  27. Wymienić i określić różnice pomiędzy hipotezami wytrzymałościowymi
  28. Które hipotezy należy stosować w przypadku materiałów kruchych, a które w przypadku materiałów plastycznych?
  29. Co rozumiemy pod pojęciem naprężenia zredukowanego i jak je liczymy według hipotezy Hubera?
  30. Kiedy stosujemy hipotezę Mohra?

1. Narysować  wykres rozciągania dla stali niskowęglowej i zdefiniować granice wytrzymałości

2. Narysować wykres rozciągania bez wyraźnej granicy plastyczności i wyjaśnić jak określa się umowną granicę plastyczności

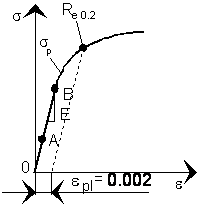
Dla materiałów plastycznych bez wyraźnej granicy plastyczności R_e wprowadzono umowną granicę plastyczności R_0,2.

Umowną granicą plastyczności nazywamy takie naprężenie, które wywołuje w próbce odkształcenie trwałe (plastyczne) wynoszące ε=0,2% (0,002).

Gdzie:
F_0,2- siła rozciągająca wywołująca w próbce odkształcenie plastyczne równe 0,2%

S₀- pole przekroju poprzecznego próbki

wyznaczone przed badaniem

Na wykresie przedstawiono krzywą rozciągania bez wyraźnej granicy plastyczności oraz sposób określania umownej granicy plastyczności.

3. Prawo Hooke'a dla jednoosiowego rozciągania. Robert Hooke stwierdził, że wydłużenie l pręta pryzmatycznego jest wprost proporcjonalne do siły rozciągającej P i do długości początkowej l pręta, a odwrotnie proporcjonalne do pola A przekroju poprzecznego pręta.

s = P / A

E - moduł sprężystości przy rozciąganiu, moduł Younga

A - pole przekroju poprzecznego

l - wydłużenie pręta

l - długość początkowa pręta

P - siła rozciągająca

σ - naprężenie rozciągające w pręcie

 - odkształcenie względne

Dla większości materiałów stosowanych w budowie maszyn prawo Hooke'a można stosować zarówno zarówno przypadku rozciągania, jak i ściskania, przy czym naprężenia rozciągające zaznaczamy znakiem plus (+), a ściskające znakiem minus (-).

4. Prawo Hooke'a przy ścinaniu

Jeżeli rozpatrzymy kostkę sześcienną w stanie czystego ścinania, to pod wpływem naprężeń tnących stwierdzimy przejście sześcianu w równoległościan. Ściany sześcianu pozostaną w dalszym ciągu płaskie, a kąty proste ulegną odkształceniu o kąt γ

Ponieważ kąt γ jest mały, przez to należy twierdzić, że krawędzie nie ulegną wydłużeniu, ani skróceniu i objętość kostki nie ulegnie zmianie, a nastąpi jedynie zmiana postaci. Dla materiału kostki podlegającego prawu Hooke'a kąt odkształcenia postaciowego γ jest proporcjonalny do naprężeń ścinających  .

γ - kąt odkształcenia postaciowego

  - naprężenia ścinające

G - moduł sprężystości postaciowej

*Dodatkowo:

Współczynnik proporcjonalności G nosi nazwę modułu sprężystości postaciowej (ścinania, skręcania, Kirchhoffa). Wartości modułów G dla różnych materiałów podaje się w tabelach.

Wartość modułu sprężystości postaciowej można też wyznaczyć z zależności:

5.Naprężenie dopuszczalne jest to wartość naprężenia nieprzekraczalna w warunkach normalnej pracy (największe naprężenie, które jest jeszcze bezpieczne dla konstrukcji).

Naprężenie dopuszczalne na rozciąganie k_r wyznacza się ze wzoru:

gdzie:

R_m - wytrzymałość na rozciąganie

n_m - współczynnik bezpieczeństwa w odniesieniu do wytrzymałości na rozciąganie R_m,

liczba większa od jedności

W wielu przypadkach należy się zabezpieczyć nie tylko przed zerwaniem danego elementu konstrukcji, lecz również przed powstaniem odkształceń plastycznych. W takich przypadkach naprężenia dopuszczalne k_r wyznacza się jako iloraz granicy plastyczności R_e przez współczynnik bezpieczeństwa n_e odniesiony do granicy plastyczności:

Obliczenie wytrzymałościowe elementu rozciąganego sprowadza się do sprawdzenia, czy spełniony jest warunek:

W podobny sposób jak dla rozciągania wyznacza się naprężenia dopuszczalne na:

• ściskanie k_c

• zginanie k_g

• skręcanie k_s

• ścinanie k_t

6. Zasada ta polega na rozbiciu danego złożonego układu obciążeń na układy proste tak dobrane, że suma ich tj. nałożenie jednych na drugie, dała rozpatrywany układ wyjściowy.

Gdyby pręt był obciążony tylko siłą P₁, wówczas wydłużenie pręta wynosiłoby:

Gdyby pręt był obciążony tylko siłą P₂, wówczas rozciągany jest tylko odcinek a pręta, dolna część poniżej punktu przyłożenia P₂ uległaby jedynie przemieszczeniu o l''

Wydłużenie całkowite

Metodę tę można stosować gdy w żadnym punkcie układu wyjściowego (zasadniczego) naprężenia nie przekraczają granicę proporcjonalności σ_prop.

Zaś nie można używać gdy działani

e jednych sił zmienia charakter działania innych sił.

Na skutek działania siły T

siła P wywołuje nie tylko ściskanie pręta, lecz również zginanie.

7. Co rozumiemy pod pojęciem układu statycznie niewyznaczalnego i co jest potrzebne do wyznaczania sił i reakcji w takim układzie?

Układ statycznie niewyznaczalny to taki, w którym liczba niewiadomych reakcji jest większa od znanej ze statyki liczby warunków równowagi. Układy takie są nierozwiązalne na gruncie statyki ciał doskonale sztywnych.

Rozwiązać taki układ można dopiero wówczas, gdy uwzględni się odkształcenia ciał wchodzących w skład danego układu. Odkształcenia układu przyjmujemy dowolnie (byleby zgodnie z nałożonymi więzami), natomiast reakcje więzów muszą odpowiadać przyjętym odkształceniom. Jeżeli więc przyjmujemy, że pręt ulega wydłużeniu, to musi w nim występować siła rozciągania (jeżeli skróceniu-siła ściskania).

Przykład jest na str. 14 w skrypcie, nie wiem czy ktoś będzie chciał to na kole rysować i wyliczać

Inna definicja: „Układy statycznie niewyznaczalne - są to układy, dla których z równań równowagi otrzymuje się nieskończenie wiele rozwiązań na siły reakcji. W takim przypadku liczba reakcji jest większa od liczby niezależnych równań równowagi, oraz liczba stopni swobody układu jest równa zeru.”

8. Wyprowadzić wzór na naprężenia obwodowe w pierścieniu poddanym działaniu ciśnienia wewnętrznego.

9.Co rozumiemy pod pojęciem energii potencjalnej odkształcenia plastycznego i jak ją obliczamy?

energia potencjalna ciała odkształconego sprężyście jest to energia którą doskonale tłumaczy działanie sprężyny : W celu rozciągnięcia sprężyny trzeba wykonać pracę, z kolei sprężyna kurcząc się będzie nam tę pracę oddawać. Tak więc w rozciągniętej sprężynie jest zgromadzona energia sprężystości (równoważna pracy użytej do jej praca jej rozciągania), zaś uwolnienie tej energii pozwala na odzyskanie włożonej poprzednio pracy. Na tej zasadzie działają m.in. naręczne zegary mechaniczne (nakręcane), zabawki, gumowe proce, a także łuki i kusze.

Energia sprężystości zgromadzona w rozciągniętej sprężynie zależy od:

1)rozciągnięcia x

2)Stałej sprężystości k

Zależności te połączono wzorem:
. Wzór ma zastosowanie przy niezbyt dużych rozciągnięciach x. Wzór powyższy obowiązuje nie tylko dla rozciągania, ale i dla ściskania, odchylania i uginania i ogólnie dla odkształceń od położenia równowagi.

  10. Określić rozkład i znaki naprężeń występujących w jednokierunkowym stanie napięcia, na płaszczyznach nachylonych pod kątami  , (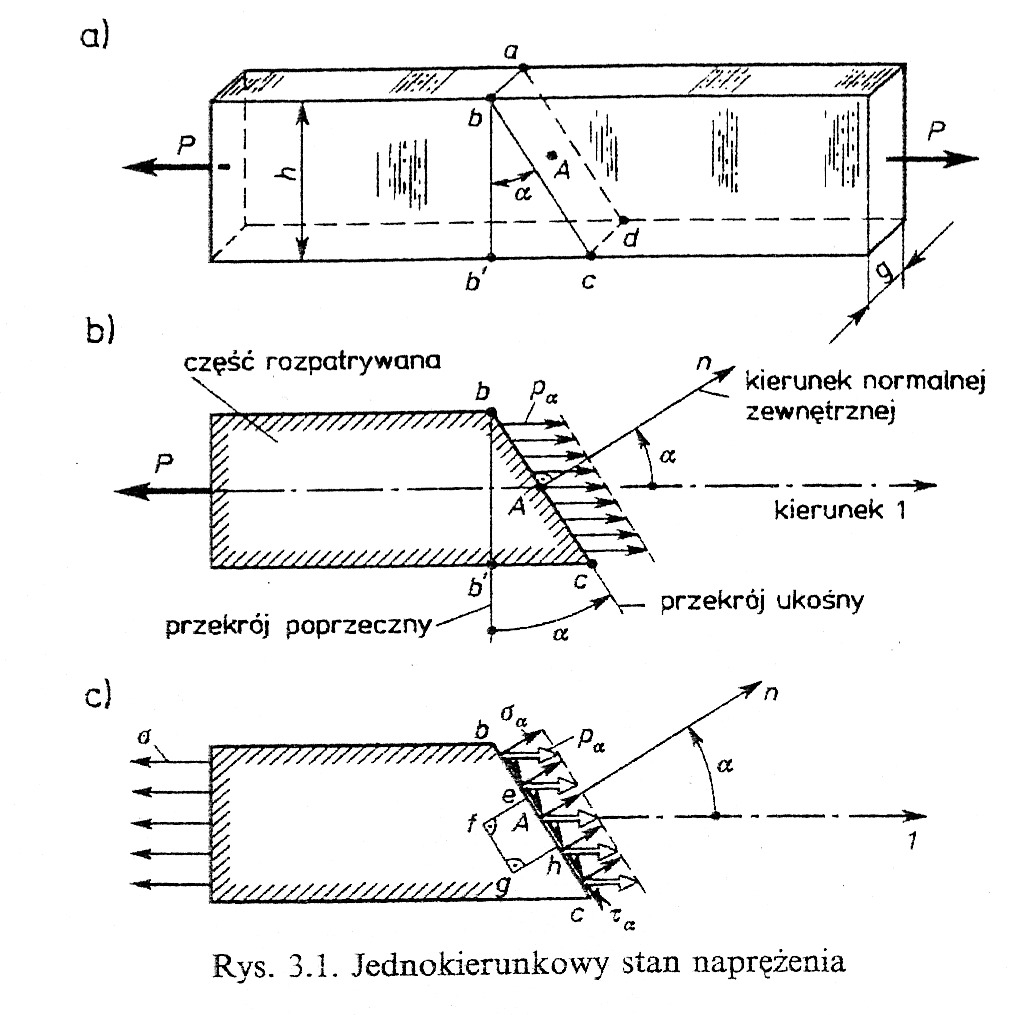
+90^o), ( ^

Suma rzutów na kierunek 1 sił działających w prętach na rozpatrywaną część pręta

Pole F_ ukośnego przekroju abcd wynosi F_=gh/cos

Dla =0 naprężenia p_ stają się równe naprężeniom rozciągającym

Rozłóżmy p_ na dwa kierunki, a otrzymane składowe oznaczmy
.
po wykorzystaniu wcześniejszych zależności i podstawieniu tożsamości sin2 2 sin cos

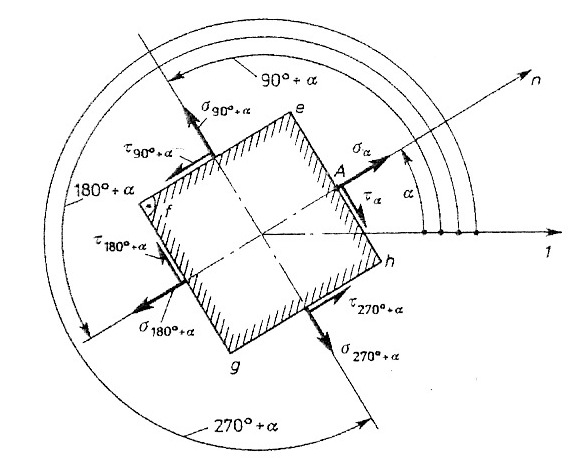
Dodatni kąt  odmierzany jest od kierunku 1do kierunku normalnej (przeciwnie do kierunku ruchu wskazówek zegara).

Dla przekrojów f-g i g-h

Dla przekroju e-f otrzymujemy:

11. Podać wzory na naprężenia normalne i styczne dla dwuosiowego (płaskiego) stanu naprężenia

12. Określić zasady konstruowania koła Mohra  dla płaskiego stanu naprężenia (dane s1 i s2).

13. Narysować rozkład naprężeń i koło Mohra dla płaskiego stanu naprężenia.

14. Dane są naprężenia sx i sy oraz t. Zastosować koło Mohra w celu wyznaczenia naprężeń głównych  s1 i s2.

15. Liczba Poissona

symbol ν. Współczynnik różny dla różnych substancji określający ich zachowanie podczas rozciągania. Przy rozciąganiu elementarnej kostki sześciennej, w czasie gdy jeden bok ulega wydłużeniu, dwa inne ulegają proporcjonalnemu skracaniu. Jest to bezwymiarowa stała materiałowa, określająca stosunek (bezwzględną wartość stosunku) odkształceń poprzecznych do odkształcenia podłużnego (osi pręta) dla rozciągania; dla realnych materiałów waha się w granicach od 0 do 0.5 (0 korek, 0.5 - guma), stal ok. 0.27, beton ok. 0.16

gdzie: ε - odkształcenie, n - dowolny kierunek prostopadły do m

L'=L+∆L

d'=d+∆d (przy wydłużaniu pręta ∆d będzie ujemna)

Jeżeli pręt o średnicy d (lub dowolnym innym charakterystycznym wymiarze, np. szerokości) i długości L zostanie poddany rozciąganiu tak, że wydłuży się o ΔL, to jego średnica zmieni się (zmniejszy się, stąd dla uniknięcia wartości ujemnych współczynnika znak minus we wzorze) :

16. Jak określamy odkształcenia w płaskim stanie napięcia

  17. Podać prawo Hooke'a dla dwukierunkowego stanu napięcia

18. Uogólnione prawo Hooke'a

Opisuje związki między odkształceniami i naprężeniami, w przypadku ciała izotropowego.

Rozwiązując powyższe równania względem naprężeń otrzymujemy związki:

W tych wzorach E oznacza moduł sprężystości podłużnej (moduł Younga), G moduł sprężystości poprzecznej (moduł Kirchoffa), zaś v współczynnik Poissona

Wzory są słuszne, gdy żadne z naprężeń nie przekroczyło granicy proporcjonalności (tj. granicy stosowalności prawa Hooke'a)

19. Czyste ścinanie- stan obciążenia w którym na ścianach rozpatrywanego elementu nie występują żadne inne

naprężenia oprócz naprężeń tnących.

Efekt ten można uzyskać wywołując np. rozciąganie i ściskanie takimi samymi co do wartości bezwzględnej

naprężeniami s działającymi w dwóch wzajemnie prostopadłych kierunkach.

Jeżeli rozpatrywany element przetniemy( w myśli) przekrojem a-b określonym normalną nachyloną do osi głównej

pod kątem a=p/4 to zgodnie ze wzorem sa=s1 cos2a + s2sin2a naprężenie normalne dla s1=+s oraz

s2=-s będzie równe zeru:

Natomiast naprężenie styczne wg wzoru ta= _

_(s1-s2) sin2a wyniesie:

20. Zależność miedzy modułami E i G:

• Moduł Kirchhoffa (G) (moduł sprężystości poprzecznej) - współczynnik uzależniający odkształcenie postaciowe materiału od naprężenia, jakie w nim występuje. Jest to wielkość określająca sprężystość materiału.

G =
gdzie:
,

• Moduł Younga (E) (moduł sprężystości podłużnej) (w układzie jednostek SI) - wielkość określająca sprężystość materiału.

E =
gdzie: ε - względne odkształcenie liniowe, σ - naprężenia

Moduł Kirchhoffa dla materiałów izotropowych bezpośrednio zależy od modułu Younga i współczynnika Poissona:

G =
; E = 2G
(1+

21.Gdy mamy przypadek, w którym występują naprężenia styczne (tnące) i normalne, gdzie stycznie >> normalne, to warunek bezpieczeństwa sprowadza się do sprawdzenia, czy naprężenia tnące nie przekraczają wartości naprężeń dopuszczalnych na ścinanie k_t.

Sposób omówiony na przykładzie [rys]:

Sworzeń łączący płaskownik środkowy o grubości g, z dwoma jednakowymi płaskownikami (grubość h).

Płaskownik środkowy poddany jest działaniu siły rozciągającej: P, dzięki czemu płaskownik górny i dolny będzie rozciągany siłą 0,5P (przez połączenie sworzniem). Jeśli wartość P będzie zwiększana, to w końcu dojdzie do stanu, w którym sworzeń ulegnie zniszczeniu- przez poślizg/ścięcie (rys 4.4b).

W przekrojach, które ulegną ścięciu działają siły równe T₁ i T₂ (rys 4.4c), które są równe: T₁=T₂=0,5P.

W wyniku działania tych sił, powstają naprężenia tnące
(rys 4.4d). Rozkład tych naprężeń na przekrojach poprzecznych sworznia nie jest równomierny, ale stosuje się pojęcie średniej wartości naprężenia tnącego równej:
,

gdzie:

T- siła tnąca w danym przekroju poprzecznym,

F- pole powierzchni przekroju poprzecznego.

Warunek wytrzymałości elementu ścinanego wyraża się:

Pod działaniem siły P ulegają jednoczesnemu ścinaniu 2 przekroje poprzeczne sworznia, zatem siła tnąca w każdym przekroju jest równa 0,5P, a średnie naprężenie tnące:

Uproszczony sposób obliczeń na ścinanie przeprowadza się zazwyczaj dla połączeń nitowanych, śrubowych, klinowych, spawanych.

22. OBLICZANIE WYTRZYMAŁOŚCI WAŁU PEŁNEGO

Wały- pręty obracające się w czasie pracy i przenoszące momenty skręcające.

Naprężenia maksymalne występujące w pręcie skręcanym:

Wskaźnik wytrzymałości na skręcanie:

Jo- biegunowy moment bezwładności,

g_max- odległość najdalszego włókna od osi pręta.

Aby skręcany pręt mógł pracować bezpiecznie, max naprężenia tnące nie mogą przekroczyć naprężeń dopuszczalnych na skręcanie ks:
(warunek wytrzymałościowy)

zgodnie ze wzorem:
dla wału okrągłego Wo:

Warunek sztywności:

wiedząc że:
, to kąt skręcania przypadający na jednostkę długości wału nie może być większy od dopuszczalnego kąta skręcania
:

23. Moment bezwładności to miara bezwładności ciała w ruchu obrotowym względem określonej, ustalonej osi obrotu. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość kątową. Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od rozmieszczenia masy w ciele. Moment bezwładności ma wymiar
. Zwykle mierzy się go w kg·m². Moment bezwładności punktu materialnego jest iloczynem jego masy i kwadratu odległości od osi obrotu:
, gdzie: m- masa punktu; r - odległość punktu od osi obrotu.

  24. Koło Mohra dla momentów bezwładności.

25. Definicja sił nornalnych, tnących, mometów gnących

ODPOWIEDZI 23, 25, 26, 27, 28, 29 są na zdjęciach poniżej:

26. Co rozumiemy pod pojęciem belki o równomiernej wytrzymałości na zginanie?

  27. Wymienić i określić różnice pomiędzy hipotezami wytrzymałościowymi

  28. Które hipotezy należy stosować w przypadku materiałów kruchych, a które w przypadku materiałów plastycznych?

  29. Co rozumiemy pod pojęciem naprężenia zredukowanego i jak je liczymy według hipotezy Hubera?

30. Mohra hipoteza [h. mo:ra], mech. jedna z hipotez wytrzymałościowych; Ch.O. Mohr rozszerzył hipotezę największego naprężenia stycznego na materiały o różnej wytrzymałości na rozszerzanie i ściskanie.

---