Opis zadania

Dla zadanych warunków gruntowych należy zaprojektować skarpę równostateczną i sprawdzić jej stateczność przy zadanym obciążeniu.

Obciążenie wynosi 0,22 MN/m.

Warunki wodne: nie występuje woda gruntowa.

Warstwa nr 1: Piasek średni

miąższość warstwy: 1,0 m

grunt średnio zagęszczony, mało wilgotny

Warstwa nr 2: Piasek drobny

miąższość warstwy: 2,0 m

grunt średnio zagęszczony, mało wilgotny

Warstwa nr 3: Glina

miąższość warstwy: 4,5 m

grunt w stanie twardoplastycznym

Warstwa nr 4: Ił

miąższość warstwy: ∞

grunt w stanie twardoplastycznym

Parametry geotechniczne (ρ, _u, c_u, stan gruntu itp.) przyjmuję z normy PN-81/B-03020.

Projekt skarpy równostatecznej wg Masłowa

Hipoteza Coulomba: _f = σ_n⋅tg _u + c_u

tg  = tg _u + c_u/σ_n

1 P_S 1,0m

2 P_D 2,0 m

3 1,0 m

4 G 1,0 m

5 1,0 m

6 1,0 m

7 0,5 m

8 0,5 m

I

Warstwa 1 - P_S:

I_D = 0,35, S_r = 0,1 mało wilgotny, średnio zagęszczony ρ₁ = 1,7 t/m³

γ1 = ρ1⋅g = 16,68 kN/m3, u1 = 1 = 32°

Warstwa 2 - P_D:

I_D = 0,55, S_r = 0,3 mało wilgotny, średnio zagęszczony ρ₂ = 1,65 t/m³

γ2 = ρ2⋅g = 16,19 kN/m3, u2 = 2 = 31°

Warstwa 3 - G:

I_L = 0,2 twardoplastyczny ρ₃ = 2,15 t/m³ γ₃ = ρ₃⋅g = 21,09 kN/m³, _u3 = 18°,

c_u3 = 32 kPa, σ_zγ3 = 1⋅16,68 + 2⋅16,19 + 1⋅21,09 = 70,15 kPa

tg ₃ = tg _u3 + c_u3/σ_zγ3 = tg 18° + 32/70,15 = 0,781085 ₃ = 38°

Warstwa 4 - G

- || - , σ_zγ4 = 1⋅16,68 + 2⋅16,19 + 2⋅21,09 = 91,24 kPa

tg ₄ = tg _u3 + c_u3/σ_zγ4 = tg 18° + 32/91,24 = 0,675643 ₄ = 34°

Warstwa 5 - G

- || - , σ_zγ5 = 1⋅16,68 + 2⋅16,19 + 3⋅21,09 = 112,33 kPa

tg ₅ = tg _u3 + c_u3/σ_zγ5 = tg 18° + 32/112,33 = 0,609795 ₅ = 31°

Warstwa 6 - G

- || - , σ_zγ6 = 1⋅16,68 + 2⋅16,19 + 4⋅21,09 = 133,42 kPa

tg ₆ = tg _u3 + c_u3/σ_zγ6 = tg 18° + 32/133,42 = 0,564765 ₆ = 29°

Warstwa 7 - G

- || - , σ_zγ7 = 1⋅16,68 + 2⋅16,19 + 4,5⋅21,09 = 143,97 kPa

tg ₇ = tg _u3 + c_u3/σ_zγ = tg 18° + 32/143,97 = 0,547188 ₇ = 29°

Warstwa 8 - I

I_L = 0,1 twardoplastyczny, ρ₈ = 2,0 t/m³ γ₈ = ρ₈⋅g = 19,62 kN/m³, _u8 = 12°,

c_u8 = 54 kPa, σ_zγ8 = 1⋅16,68 + 2⋅16,19 + 4,5⋅21,09 + 0,5⋅19,62 = 153,78 kPa

tg ₈ = tg _u8 + c_u8/σ_zγ = tg 12° + 54/153,78 = 0,563708 ₄ = 29°

Rysunek na następnej stronie.

_GEN otrzymuje się przez połączenie krawędzi górnej i dolnej skarpy odcinkiem linii prostej.

Sprawdzenie stateczności skarpy metodą Felleniusa

Założenie: potencjalne powierzchnie poślizgu są walcowe. Dla danej skarpy istnieje jedna najbardziej niebezpieczna powierzchnia poślizgu, charakteryzująca się najmniejszym współczynnikiem pewności F.

Obliczenia prowadzi się

z uwzględnieniem

schematu:

Na każdy blok badanej bryły działają następujące siły:

W_i = G_i + Q_i - ciężar bloku i + obciążenie zadane rozłożone na szerokości bloku i,

P_i, P_i+1 - siły o nieznanej wartości, działające na pionowe ścianki bloku i, równoległe do podstawy bloku,

N_i = W_i⋅cos _i - składowa normalna siły W_i,

B_i = W_i⋅sin _i - składowa styczna siły W_i,

T_i = N_i⋅tg _i + li⋅ci - siła oporu tarcia i kohezji gruntu, przeciwstawiająca się sile zsuwającej.

Siły P_i pomija się.

Moment sił obracających bryłę względem punktu O:

M_obr = _i=1ⁿ B_i⋅R

Moment sił utrzymujących bryłę:

M_­u = _i=1ⁿ T_i⋅R

Współczynnik pewności wyznacza się jako stosunek M_u do M_obr:

F = M_u/M_obr = Ti/B_i

Analiza stateczności skarpy o danym konturze powinna sprowadzać się do ustalenia drogą kolejnych prób takiej powierzchni poślizgu, która dałaby najmniejszy współczynnik pewności F_min. Powinien być również spełniony warunek:

F_min ≥ F_dop.

Wartości F_dop przy stosowaniu metody Felleniusa przyjmuje się w granicach 1,1 ÷ 1,3.

Obliczenia przeprowadzone na arkuszu kalkulacyjnym.

Metoda wyznaczenia prostej, na której jest środek obrotu odpowiadający F_min - wg książki „Zarys geotechniki” Z. Wiłuna (p. rysunek).

Obliczenie F_min

Xi [m]	F(Xi)
0	3,38
6,01	2,91
9,28	3,63

Dalsze obliczenia - za pomocą kalkulatora TI 92PLUS:

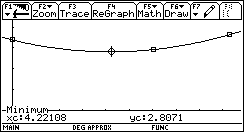
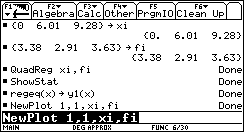
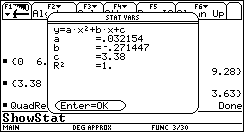
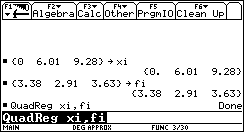
A zatem minimum funkcji F(X) znajduje się w punkcie X = 4,22108m i wynosi: F_min = 2,8071

Wniosek: skarpa może przenieść większe obciążenie niż zadane lub może być bardziej stromo nachylona.

---