Zaliczenie:

laboratorium +elaborat (zadanie z ruchu płaskiego)

Kinematyka bryły materialnej

Rzuty prędkości dowolnych dwóch pkt. ciała sztywnego na prostą przechodzącą przez te punkty są sobie równe.

Ruch postępowy bryły materialnej

Niech bryła porusza się tak, że jej położenia chwilowe są równoległe do położenia początkowego.
Taki ruch nazywać będziemy ruchem postępowym

W ruchu postępowym tor dowolnego pkt. jest taki sam jak tor innego pkt. Tory (trajektorie) punktów bryły są przesunięte równolegle względem siebie mogą być krzywymi lub prostymi (ruch prostoliniowy).

Prędkości wszystkich pkt. bryły poruszającej się ruchem postępowym są w danej chwili wektorami równymi.

Przyspieszenia wszystkich pkt. bryły poruszającej się ruchem postępowym są w danej chwili wektorami równymi.

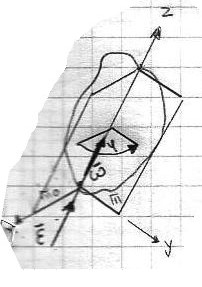
Rozpatrzmy ruch bryły mającej dwa pkt. nieruchome. W takim przypadku bryła może jedynie obracać się dookoła osi przechodzącej przez te dwa pkt. Oś ta zwana jest osią obrotu.

Ciało wykonujące ruch obrotowy ma jeden stopień swobody. Do określenia położenia tego ciała w przestrzeni potrzebna jest tylko jedna współrzędna

Torami pkt ciała są okręgi położone w płaszczyznach prostopadłych do osi obrotu o środkach leżących na osi obrotu.

Promienie tych okręgów są równe odległości od osi obrotu.

Kąt który tworzy płaszczyzna ruchoma
nie ruchomą płaszczyzną
nazywamy kątem obrotu ciała.

Kąt ten określa położenie ciała sztywnego w przestrzeni.

Kąt obrotu ciała będziemy uważali za dodatni jeżeli patrząc z grotu osi ciało obracać się będzie przeciwnie do ruchu wskazówek zegara.

Kąt obrotu jest funkcją czasu.

[rad] - kąt obrotu ciała

Pierwsza pochodna kąta obrotu względem czasu nazywamy prędkość kątową ruchu obrotowego. Prędkość kątowa to wektor leżący na osi obrotu ciała. Zwrot wyznaczamy z reguły śruby prawoskrętnej biorąc pod uwagę kierunek obrotów. Moduł wektora prędkości kątowej wynosi:

Drugą pochodną kąta obrotu nazywamy przyspieszeniem kątowym ruchu obrotowego. Przyspieszenie kątowe to wektor leżący na osi obrotu ciała.

Zwrot zgony ze zwrotem wektora prędkości kątowej gdy ruch jest przyspieszony lub zwrot przeciwny do zwrotu wektora prędkości kątowej gdy ruch jest opóźniony.

Moduł wektora przyspieszenia kątowego wynosi:

- kąt obrotu

- prędkość kątowa

- przyspieszenie kątowe

Prędkość liniowa punktu bryły w ruchu obrotowym jest równa iloczynowi wektorowemu prędkości kątowej ruchu obrotowego bryły sztywnej przez promień wektora łączący dowolny punkt na osi obrotu bryły z rozpatrywanym punktem.

Prędkość punktu bryły

Rozkład prędkości punktów

Przyspieszenie punktu bryły po materialnej

Całkowite przyspieszenie dowolnego punktu bryły sztywnej poruszającej się ruchem obrotowym jest wektorowa suma dwóch przyspieszeń: przyspieszenia stycznego (obrotowego) i normalnego (poosiowego, dośrodkowego)

Przyspieszenie styczne punktu bryły

Wartość wektora:

Kierunek wektora przyspieszenia stycznego jest kierunkiem stycznym do toru rozpatrywanego punktu. Zwrot zależy od tego czy ruch jest przyspieszony czy opóźniony. Jeżeli jest przyspieszony jest zgodny ze zwrotem wektora prędkości rozpatrywanego punktu. Jeżeli jest opóźniony to zwrot wektora przyspieszenia stycznego jest przeciwny.

Przyspieszenie normalne punktu bryły

wartość wektora:

Kierunek wektora przyspieszenia normalnego jest prostopadły do kierunku wektora prędkości kątowej (prostopadły do osi obrotu) i prostopadły do wektora prędkości liniowej rozpatrywanego punktu czyli pokrywa się z promieniem okręgu po którym w danej chwili porusza się rozpatrywany punkt.

Zwrot zawsze do osi obrotu.

Ruch obrotowy bryły materialnej

Rozkład przyspieszeń punktów

moduł wektora:

Dla dowolnego punktu znajdującego się na promieniu możemy napisać:

dr Paweł Bachorz Mechanika 29.02.08

Semestr II Wykład 1

- 4 -

---