13. Optyka

13.6. Promieniowanie rentgenowskie.

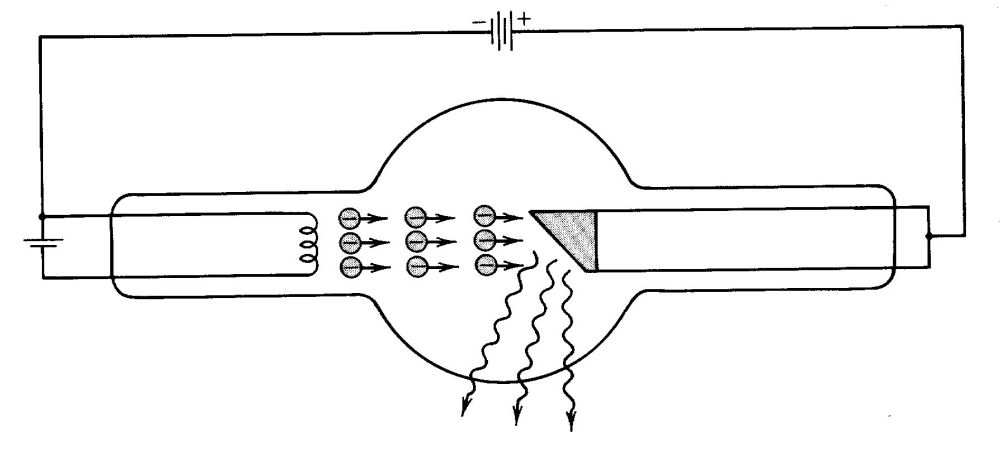
Schemat budowy lampy rentgenowskiej.

Przyspieszone do dużej prędkości elektrony uderzają w antykatodę zmniejszając swoją energię.

Energia elektronów zamienia się w energię promieniowania rentgenowskiego wskutek hamowania elektronów w polu atomów antykatody (daje to tzw. promieniowanie hamowania), lub zużywana jest na jonizację atomów antykatody.

oraz

stąd

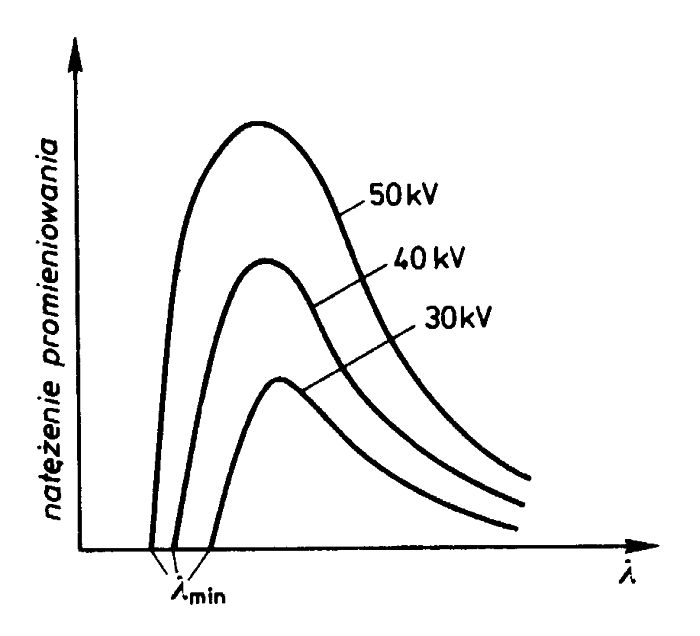
Widmo ciągłe promieniowania rentgenowskiego (promieniowanie hamowania). Przy większych napięciach przyspieszających natężenie jest większe, ale zawsze istnieje minimalna długość promieniowania ၬ_gr (tzw. krótkofalowa granica promieniowania rentgenowskiego) ograniczająca widmo.

Podczas jonizacji atomów antykatody, atomy wzbudzone przez wiązkę elektronów przechodzą do stanów o mniejszej energii wysyłając fale elektromagnetyczne o określonych (zależnych o materiału antykatody) długościach fali. Jest to tzw. promieniowanie charakterystyczne, które nakłada się na widmo ciągłe.

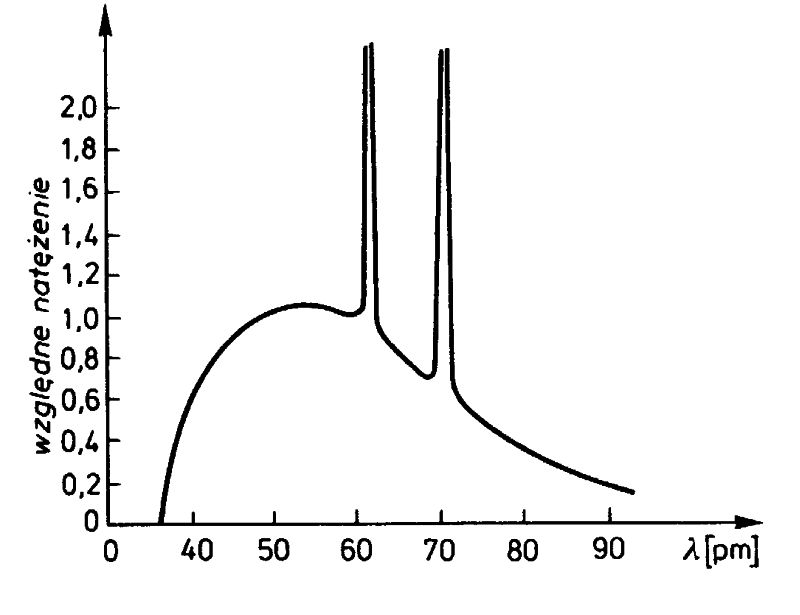
Przykładowe widmo rentgenowskiego promieniowania charakterystycznego. Od lewej - serie linii K oraz L.

Prawo Moseley'a:

Gdzie: A - stała; Z - liczba porządkowa w układzie okresowym

Pierwiastki ciężkie Z > 62

emitują linie K, L, M

Pierwiastki lekkie 8 < Z < 32

emitują tylko linię K

widmo ciągłe - zastosowanie w medycynie

widmo charakterystyczne - badania struktury atomowej

13.7. Dyfrakcja promieniowania rentgenowskiego (prawo Bragga).

Promienie ugięte przechodzą przez polikrystaliczną próbkę wzdłuż tworzących stożków koncentrycznych, dając na kliszy układ współśrodkowych pierścieni. Tworzące nachylone są pod kątem 2θ do kierunku wiązki pierwotnej.

Atomy tworzą 3-wymiarową siatkę dyfrakcyjną.

Dyfraktogram Lauego (1912)

Obraz dyfrakcji promieniowania rentgenowskiego na monokrysztale berylu. Tzw. obraz Lauego powstaje wskutek ugięcia promieni tak, że odległość płaszczyzn atomowych i kąt padania θ spełniają prawo Bragga.

Badając rozmieszczenie i natężenie punktów możemy odtworzyć strukturę kryształu.

Prawo dyfrakcji Bragga: 2d⋅sinθ = mλ gdzie m = 1, 2, …

Aby otrzymać wzmocnienie w kierunku określonym przez kąt θ, promienie odbite od rodziny płaszczyzn muszą się wzmacniać. Oznacza to, że różnica dróg wiązek odbitych musi być równa całkowitej wielokrotności λ ⇒ Δ = mλ

92

62

32

8

M

L

K

ν = c/λ

Z

a₀ = 5,627 Å

---