Iloczyn skalarny (iloczyn hermitowski, forma hermitowska dodatnia) w przestrzeni wektorowej V nad ciałem K (C liczby zespolone lub R liczby rzeczywiste) nazywamy takie odwzorowanie

1.
(dodatnia określoność)

2. (αx + βy | z) = α(x | z) + β(y | z), gdzie
oraz
(liniowość)

3.
, gdzie
jest sprzężeniem zespolonym (symetryczność) W geometrii euklidesowej trójwymiarowej klasyczna definicja iloczynu skalarnego związana jest z kątem między wektorami w przestrzeni:

,

gdzie
oznacza długość wektora
. Widać stąd, że jeżeli wektory
są prostopadłe, to ich iloczyn skalarny jest równy 0. Zachodzi także zależność odwrotna: jeśli iloczyn skalarny dwu niezerowych wektorów jest równy zero, to są prostopadłe.

loczyn wektorowy to działanie (n − 1)-argumentowe na elementach n-wymiarowej przestrzeni euklidesowej. Niech V będzie n-wymiarową przestrzenią euklidesową o zadanej orientacji. Iloczynem wektorowym wektorów
nazywamy wektor
taki, że

Jeśli
są liniowo zależne, to β jest wektorem zerowym.

Jeśli
są liniowo niezależne

(ortogonalne dopełnienie podprzestrzeni)

(pierwiastek z wyznacznika Grama)

Baza
jest zorientowana dodatnio.

Działanie to oznaczamy

Jeżeli
i
, to iloczyn wektorowy tych wektorów jest wektorem
takim, że:

wartość wektora wynikowego jest równa iloczynowi wartości
obu wektorów wyjściowych pomnożonego przez sinus kąta między nimi zawartego:
,

otrzymany wektor jest prostopadły do płaszczyzny wyznaczonej przez mnożone wektory,

zwrot ustalamy przy pomocy reguły śruby prawoskrętnej lub reguły prawej dłoni,

ściślej rzecz biorąc, iloczyn wektorowy jest pseudowektorem, ponieważ jego współrzędne transformują się przy obrotach układu współrzędnych jak współrzędne wektora, ale nie zmieniają znaku przy odbiciu osi.

Gradient wybranej wielkości (np. temperatury) jest wielkością określającą szybkość i kierunek największej zmiany wielkości.

Wektor przeciwny gradientowi nazywany jest antygradientem.

Gradient - to operator różniczkowy, który działając na pole skalarne, tworzy pole wektorowe. Utworzone pole wektorowe ma kierunek i zwrot największego wzrostu funkcji w danym punkcie, a wartość jest proporcjonalna do szybkości wzrostu (wzrost na jednostkę długości) funkcji. Gradient określony na polu wektorowym daje pole tensorowe.

Gradient oznaczany jest `grad' lub odwróconym trójkątem (operator nabla):
zwanym nabla.

W układzie współrzędnych kartezjańskich wektor gradientu jest określony jako:

gdzie
są wersorami osi kartezjańskiego układu współrzędnych.

Nabla - operator różniczkowy traktowany w operacjach rachunkowych jak symboliczny wektor. Pozwala zapisać operacje różniczkowe na funkcjach w prostej i zwartej formie działań wektorów.

W trójwymiarowym, kartezjańskim układzie współrzędnych:

gdzie
to wektory bazowe czyli wektory jednostkowe (wersory) o kierunkach i zwrotach zgodnych z kolejnymi osiami (X,Y, Z) układu współrzędnych w R3.

Dywergencja - operator różniczkowy, który danemu polu wektorowemu przypisuje pole skalarne.

Funkcję:

Będziemy nazywać polem wektorowym w przestrzeni trójwymiarowej. Dalej będziemy zakładać że powyższa funkcja jest różniczkowalna w całej swej dziedzinie (dzięki temu mamy pewność o istnieniu pochodnych cząstkowych).

Dywergencja pola wektorowego
jest skalarnym operatorem różniczkowym, określonym następującą formułą:

Gdzie
jest obszarem w przestrzeni,
brzegiem tego obszaru (czyli pewną powierzchnią zamkniętą), a | S | oznacza pole powierzchni S.

Całka podwójna występująca w definicji nosi nazwę strumienia pola wektorowego
po powierzchni S.

Rotacja (wirowość) - operator różniczkowy działający na pole wektorowe
, tworzy pole wektorowe wskazujące wirowanie (gęstość cyrkulacji) pola wyjściowego. Oznaczana jest przez
lub
(z ang. rotacja), czasami również zapisywana jako dF.

Jeżeli rotacja danego pola wektorowego jest równa zero (wektorem zerowym), to pole to jest bezwirowe. Pole bezwirowe posiada potencjał (i odwrotnie: pole posiadające potencjał jest polem bezwirowym).

Rotację definiuje się jako iloczyn wektorowy operatora nabla
i wektora
:

.

Wektor wodzący - dla danego punktu A to wektor zaczepiony w początku układu współrzędnych i o końcu w punkcie A, czyli np. w układzie kartezjańskim:

Długość wektora wodzącego jest odległością punktu od początku układu współrzędnych.

rędkość liniowa w ruchu jednostajnym prostoliniowym [edytuj]

Prędkość w ruchu jednostajnym prostoliniowym jest stała (zarówno jej kierunek i wartość). Przyjmujemy odtąd, że do położenia ciała wystarczy jedna współrzędna x. Każdy ruch prostoliniowy można przez odpowiednie obroty sprowadzić do przypadku jednowymiarowego. Prędkość w ruchu jednostajnym prostoliniowym określa więc następująca zależność:

Gdzie:

- wektor położenia jako funkcja czasu t

S - przebyta droga

T - czas trwania ruchu

x(t) - funkcja położenia (skalar) od czasu

Prędkość liniowa w ruchu jednostajnie przyspieszonym

Przyspieszenie
jest stałe i niezerowe, więc prędkość
zmienia się. W ruchu tym także można ograniczyć się do rozpatrywania jednej współrzędnej.

Gdzie:

T - całkowity czas ruchu

- wektor prędkości jako funkcja czasu.

Czasami (zazwyczaj z powodów dydaktycznych) wyróżnia się specjalny przypadek ruchu jednostajnie przyspieszonego prostoliniowego - ruch jednostajnie opóźniony prostoliniowy. W ruchu tym wektor przyspieszenia
jest stały i skierowany przeciwnie do wektora prędkości początkowej -
.

Przyspieszenie - wektorowa wielkość fizyczna wyrażająca zmianę prędkości w czasie. Jeżeli mamy dany wektor
określający położenie punktu materialnego i wektor
określający prędkość tego punktu, to przyspieszenie
tego punktu obliczamy w następujący sposób:

Jednostka przyspieszenia w układzie SI to metr na sekundę do kwadratu.

Przyspieszenie dośrodkowe

Jest to składowa przyspieszenia prostopadła do toru ruchu. Reprezentuje tę część przyspieszenia, która wpływa na kierunek prędkości, a zatem na kształt toru. Jeżeli prędkość chwilowa oznaczona jest jako v, a promień chwilowego zakrzywienia toru (promień okręgu stycznego do toru) ruchu wynosi r, to wartość an przyspieszenia dośrodkowego ciała jest równa:

Przyspieszenie styczne

Jest to składowa przyspieszenia styczna do toru ruchu, wpływająca na wartość prędkości. Stosując oznaczenie v dla wartości prędkości chwilowej i oznaczenie s dla drogi pokonanej przez ciało, przyspieszenie styczne as określają wzory:

Przyspieszenie kątowe

Występuje w ruchu obrotowym - jest wektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt α, a wartość prędkości kątowej oznaczymy jako ω, to wartość przyspieszenia kątowego ε wynosi:

Jednostka przyspieszenia kątowego w układzie SI to jeden radian przez sekundę do kwadratu.

Prędkość kątowa - w fizyce wielkość opisujaca ruch po okręgu (ruch obrotowy). Jest wektorem (pseudowektorem) leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej.

Jeśli współrzędna kątowa ciała określa kąt θ to wartość prędkości kątowej ω jest równa:

Jednostka prędkości kątowej w układzie SI to jeden przez sekundę.

Zależność prędkości liniowej V ciała poruszającego się po okręgu o promieniu r od prędkości kątowej ω tego ciała dana jest wzorem:

V=ω•r

Pęd punktu materialnego jest równy iloczynowi masy [m] i prędkości [v] punktu. Pęd jest wielkością wektorową; kierunek i zwrot pędu jest zgodny z kierunkiem i zwrotem prędkości.

W układzie SI jednostka pędu nie ma odrębnej nazwy, a jest określana za pomocą jednostek prostszych, np. niuton·sekunda (N·s) lub kilogram·metr/sekunda (kg·m/s).

Moment pędu (inaczej kręt) wielkość fizyczna opisująca ruch ciała, zwłaszcza ruch obrotowy.

W tradycyjnej matematyce moment pędu jest wielkością wektorową (pseudowektor). Moment pędu punktu materialnego względem zadanego punktu określony jest zależnością:

gdzie

L to moment pędu punktu materialnego,

r to wektor łączący punkt, względem którego określa się moment pędu i punkt ciała,

p to pęd punktu materialnego

iloczyn wektorowy wektorów.

Powyższy wzór można wyrazić:

gdzie θr,p jest kątem między r i p

Dla ciała obracającego się:

gdzie:

I to moment bezwładności ciała,

ω to prędkość kątowa.

Moment siły (moment obrotowy) -
siły
względem punktu O jest iloczyn wektorowy promienia wodzącego
, o początku w punkcie O i końcu w punkcie przyłożenia siły oraz siły
:

Wektor momentu siły jest wektorem osiowym (pseudowektorem), zaczepiony jest w punkcie O, a jego kierunek jest prostopadły do kierunku płaszczyzny wyznaczonej przez wektory
i
.

Określa się także moment siły względem osi, jest on równy rzutowi wektora momentu siły na tę prostą. Współrzędne Mxf, My i Mz wektora
nazywają się momentami siły względem odpowiednich osi x, y i z.

Jednostką momentu siły jest
. Jednostka ta jest zdefiniowana analogicznie, jak dżul, czyli jednostka energii.

I zasada dynamiki (zasada bezwładności)

Jeżeli na ciało nie działa żadna siła lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym (po prostej ze stałą prędkością).

II zasada dynamiki

Gdy siły działające na ciało nie równoważą się, to ciało porusza się ruchem zmiennym. Kierunek i zwrot tego przyspieszenia są zgodne z kierunkiem siły wypadkowej, a wartość proporcjonalna do wartości siły. Wartość przyspieszenia ciała o masie m jest wprost proporcjonalna do wartości wypadkowej siły działającej na to ciało, a jego kierunek i zwrot są zgodne z kierunkiem i zwrotem tej siły. Ciało o większej masie pod działaniem takiej siły wypadkowej uzyskujemniejsze przyspieszenie.
III zasada dynamiki

Siły wzajemnego oddziaływania na siebie 2 ciał mają takie same wartości, ten sam kierunek, przeciwny zwrot i różny punkt przyłożenia. Siły te nie równoważą się bo działają na dwa różne ciała.

Jeśli ciało A działa na ciało B siłą F (akcja), to ciało B działa na ciało A siłą (reakcja) o takiej samej wartości i kierunku, lecz o przeciwnym zwrocie.

Praca (najczęściej oznaczana literą W) to jedna z najważniejszych wielkości mechaniki. Definiuje się ją jako iloczyn skalarny wektora siły działającej na ciało i wektora przesunięcia (pod warunkiem, że przesunięcie jest prostoliniowe, a siła stała podczas przesunięcia):

W ogólnym przypadku używa się wyrażeń całkowych:

Jednostką pracy w układzie SI jest dżul (J) określany jako niuton*metr:

Wykonanie pracy może powodować zmianę energii układu.

Siła jest zachowawcza, jeśli praca przez nią wykonana w ruchu na drodze o początku A i końcu B zależy tylko od położenia punktów A i B, nie zależy zaś od przebiegu drogi, prędkości ruchu ani czasu. Biorąc dowolne A oraz B=A otrzymuje się wniosek, że siła zachowawcza na dowolnej drodze zamkniętej wykonuje pracę zerową. Zachowawczość siły można również zbadać przez policzenie jej rotacji, jeśli wynosi ona 0 to siła jest zachowawcza, jest to wniosek z twierdzenia Stokesa.

Z polem działania siły zachowawczej można zatem związać skalarne pole potencjału.

Siłami zachowawczymi są m.in. kulombowskie siły oddziaływań elektrostatycznych, siła grawitacji, siła sprężystości.

Zasada najmniejszego działania to stworzona przez Pierre Louis Maupertuisa zasada mówiąca, że w fizyce klasycznej (porównaj: fizyka kwantowa) fizycznie realizowane tory cząstek minimalizują pewien funkcjonał zwany działaniem.

Zastosowanie metody znajdowania minimum funkcjonału prowadzi do równań Eulera-Lagrange'a.

Zasada najmniejszego działania jest przykładem tak zwanego podejścia teleologicznego. Prowadzi ono do opisu zachowania się układu w sposób w którym zachowanie się układu w chwilach
zależy nie tylko od zachowania się układu w chwilach wcześniejszych, ale także od zachowania się układu w chwili np. t10 i wszelkich innych późniejszych. Jak się okazuje przy dosyć ogólnych założeniach opis taki jest równoważny opisowi za pomocą równań Eulera-Lagrange'a (choć oczywiście nie w każdych warunkach), a więc równań rózniczkowych, w których z kolei mamy do czynienia z opisem zachowania układu w sposób deterministyczny (przyczynowy) i w którym zachowanie się układu w chwili t zależy wyłącznie od zachowania się układu w chwilach wcześniejszych i, co więcej, tylko dla infinitenzymalnie krótkich czasów dt.

Równania Eulera-Lagrange'a wprowadzone przez Leonharda Eulera i Josepha Louisa Lagrange'a w 1750 roku są podstawową formułą rachunku wariacyjnego.

Pozwalają one na znalezienie torów cząstek w mechanice klasycznej (qk) jeżeli znana jest funkcja Lagrange'a (lagranżjan) opisująca ten układ:

Korzystając z zasady najmniejszego działania otrzymujemy równania postaci:

Jest to układ n równań różniczkowych cząstkowych, z których znajdujemy rozwiązania qk(t).

Wyrażenia występujące w równaniach Eulera-Lagrange'a mają swoje nazwy:

- siła uogólniona

- pęd uogólniony

Twierdzenie Noether dotyczy związku zasad zachowania z symetrią ciągłą. Twierdzenie Noether ma fundamentalne znaczenie w fizyce.

Twierdzenie to mówi, że każda ciągła symetria praw fizyki (która nie zmienia zasady wariacyjnej najmniejszego działania oraz równań ruchu opisujących układ), opisywana przez grupę Liego generuje tyle praw zachowania, ile jest niezależnych parametrów opisujących daną grupę Liego (lub generatorów grupy Liego).

Symetrie dyskretne mogą generować prawo zachowania (np. symetria inwersji
generuje zachowanie parzystości P), ale nie muszą (np. inwersja w czasie
nie generuje prawa zachowania).

Środek masy ciała lub układu ciał jest punktem, w którym skupiona jest cała masa w opisie układu jako masy punktowej. Pojęcie to jest wykorzystywane także w geometrii.

Wzór na wektor wodzący środka masy:

Powyższa zależność dla ośrodków ciągłych, zapiasana w postaci wyrażeń całkowych wiąże środek masy z rozkładem gęstości ρ w przestrzeni za pomocą zależności:

przy czym:
to wektor wodzący środka masy;

M to masa ciała;

V to objętość ciała;

ρ = ρ(x,y,z) to funkcja gęstości ciała

Dla ciała znajdującego się w jednorodnym polu grawitacyjnym środek ciężkości pokrywa się ze środkiem masy.

Gdy ciało wiruje lub drga, istnieje w tym ciele punkt, zwany środkiem masy, który porusza się w taki sam sposób w jaki poruszał by się pojedynczy punkt materialny poddany tym samym siłom zewnętrznym.

W geometrii przyjmuje się zwykle jednakową gęstość w każdym punkcie.

Współrzędne środka masy układu punktów są wówczas dane wzorem:

Współrzędne środka masy bryły:

Możliwe jest także obliczanie środka masy powierzchni dwuwymiarowych lub krzywych w przestrzeni trójwymiarowej (zob. np. wielościan dualny).

Wzór dla powierzchni przyjmuje wówczas postać:

a dla krzywych

gdzie:

S to pole powierzchni,

dS element powierzchni

L to długość krzywej

dL element krzywej

a całkowanie przebiega po całej powierzchni lub całej krzywej.

Pierwsze prawo Keplera stwierdza, że planeta porusza się wokół Słońca po elipsie, w której jednym z ognisk jest Słońce.

Dla dowolnych P1 i P2, gdzie O to Słońce.Z praw mechaniki wynika, że prawo to jest spełnione w przybliżeniu bardzo dużej masy Słońca.

Pole grawitacyjne to pole wytwarzane przez obiekty posiadające masę. Określa wielkość i kierunek siły grawitacyjnej działającej na znajdujące się w nim inne obiekty posiadające masę.

Pole opisuje się poprzez podanie natężenia pola grawitacyjnego, czyli działającej na masę jednostkową, lub potencjału grawitacyjnego. Obrazem pola grawitacyjnego są linie pola lub powierzchnie ekwipotencjalne. Kierunek i zwrot linii pola jest zgodny z kierunkiem i zwrotem sił działających na masę punktową.

Pole grawitacyjne punktu lub jednorodnej kuli jest polem centralnym, ale w odniesieniu do małej przestrzeni w porównaniu do odległości centrum grawitacji to pole może być uznane za jednorodne.

Prędkość kosmiczna - prędkość, jaką musi osiągnąć dowolne ciało (np. rakieta, statek kosmiczny), by jego energia kinetyczna pokonała grawitację Ziemi i oddaliła się na odległość umożliwiającą pozostawanie w przestrzeni kosmicznej bez dodatkowego napędu.

Pierwsza prędkość kosmiczna

(VI) (prędkość kołowa, prędkość orbitalna) - potrzebna do osiągnięcia orbity okołoziemskiej

I prędkość kosmiczna to prędkość, jaką należy nadać obiektowi, aby mógł on orbitować wokół Ziemi lub innego ciała kosmicznego.

Druga prędkość kosmiczna

(VII) (prędkość ucieczki) - potrzebna do opuszczenia orbity okołoziemskiej i osiągnięcia orbity okołosłonecznej

II prędkość kosmiczna to prędkość, jaką należy nadać obiektowi, aby wyrwał się z grawitacji danego ciała kosmicznego.

Trzecia prędkość kosmiczna

(VIII) - potrzebna do opuszczenia Układu Słonecznego

Czwarta prędkość kosmiczna

(VIV) - potrzebna do opuszczenia Drogi Mlecznej

Układ inercjalny - układ odniesienia, względem którego każde ciało niepodlegające zewnętrznemu oddziaływaniu z czymkolwiek porusza się bez przyśpieszenia (tzn. ruchem jednostajnym prostoliniowym). Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki są w nich identyczne. Identyczne są również wszystkie prawa fizyki w układach inercjalnych. Uogólnienie tej zasady na układy nieinercjalne jest podstawową treścią ogólnej teorii względności. Przykładem układu inercjalnego może być Ziemia.

Postulaty szczególnej teorii względności

Albert Einstein oparł swe rozumowanie na dwóch postulatach:

Zasadzie względności

Zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych — musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki.

Niezmienność prędkości światła

Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła światła.Z połączenia postulatów 1 i 2 dojdziemy do wniosku, że światło nie potrzebuje jakiegokolwiek ośrodka (eteru) do rozchodzenia się.

Alternatywna forma założeń Szczególnej Teorii Względności, interesująca szczególnie z teoretycznego punktu widzenia, jest oparta na następujących, prostszych założeniach: Zasada względności Galileusza: "Wszystkie układy odniesienia poruszające się względem siebie ze stałą prędkością są równoważne."

założenie że transformacja pomiędzy tak określonymi układami jest transformacją afiniczną (liniową z ewentualnie wyrazem stałym);

Transformacja Galileusza - jest to transformacja zgodna z klasycznymi wyobrażeniami o czasie i przestrzeni. Transformacja zakłada, że prędkość oraz położenie są względne. Wartości te widoczne dla dowolnego obserwatora w każdym inercjalnym układzie odniesienia mogą być różne, ale każda z nich jest prawdziwa. Jeżeli przyjmiemy, że zdarzenie w układzie inercjalnym A opisane jest współrzędnymi czasoprzestrzennymi (x,y,z,t), a w układzie inercjalnym B przemieszczającym się z prędkością v w kierunku osi x, są to odpowiednio (x',y',x',t'), to transformacja współrzędnych będzie opisana układem równań:

x' = x − vt y' = y z' = z t' = t

W bardziej ogólnym przypadku transformacja Galileusza wiąże współrzędne punktu w dwu różnych układach odniesienia (xi i x'i) równaniami:

x i x' są wektorami od początku układu współrzędnych do punktu p w jednym i drugim układzie współrzędnych, v jest prędkością z jaką poruszają się dwa układy względem siebie.

Transformacja Lorentza - przekształcenie liniowe przestrzeni Minkowskiego zachowujące odległości. Odpowiada ono obrotowi w przestrzeni euklidesowej; cechą charakterystyczną niezmienniczość przekształcenia ze względu na prędkość światła.

Transformacje Lorentza mają najprostszą postać wówczas, gdy odpowiadające sobie osie współrzędnych kartezjanskich inercjalnych układów odniesienia, nieruchomego K i poruszającego się K', są do siebie wzajemnie równoległe, przy czym układ K' porusza się ze stałą prędkością V (u) wzdłuż osi OX. Jeśli ponadto jako początek odliczania czasu w obu układach (t=0) i (t'=0) wybrany został moment, w którym początki osi współrzędnych O i O' w obu układach pokrywają się, to transformacje Lorentza są w postaci:

x' = γ(x − ut)

y' = y

z' = z

gdzie

Skrócenie Lorentza:

Ciało poruszające się z dużą prędkością ulega skróceniu w kierunku ruchu
l = l0/γ = l0√[1-(v2/c2)]

Dylatacja czasu w STW: w teorii względności efekt polegający bądź na opóźnianiu się zegara będącego w ruchu w stosunku do zegara spoczywającego w pewnym inercjalnym układzie odniesienia (kinematyczna dylatacja czasu), bądź na opóźnianiu się zegara znajdującego się w silnym polu grawitacyjnym (grawitacyjna dylatacja czasu)

W szczególnej teorii względności czas w przebiegu tego samego zjawiska może być opisany zależnościami:

gdzie:

Δt0 - upływ czasu wskazany przez zegar poruszający się,

Δt - upływ czasu wskazany przez zegar nie poruszający się ,

czynnik Lorentza,

v - względna prędkość ruchu układów

c - prędkość światła w próżni.

Relatywistyczne składanie prędkości.

(vx, vy, vz — składowe prędkości ruchu układu K' względem układu K)
v: x = x' + vxt', y = y' + vyt', z = z'  + vzt', t = t'

Zagadnienie jednoczesności w STW: Jednoczesność zdarzeń zależy od układu odniesienia, a czas nie ma charakteru absolutnego.

Relatywistyczny efekt Dopplera. Przesunięcie ku czerwieni.

Zjawisko Dopplera uwidacznia się przesunięciem linii w widmie optycznym w kierunku fioletu lub czerwieni, w zależności od tego, czy następuje zbliżenie, czy oddalenie odbiornika i źródła światła; jest też przyczyną poszerzania linii widmowych światła emitowanego przez atomy gazu wykonujące chaotyczne ruchy termiczne (poszerzenie dopplerowskie); wykorzystywane m.in. w astrofizyce do badania gwiazd podwójnych, w miernikach radiolokacyjnych (dopplerowskich)

Przesunięcie Ku Czerwieni: przesunięcie widma promieniowania ciała niebieskiego w kierunku fal długich, wynikające ze zmiany długości fali tego promieniowania mierzonej na Ziemi w porównaniu z długością fali emitowanej przez ciało; wynik zjawiska Dopplera lub poczerwienienia grawitacyjnego.
ω = 2Π/T = 2Πc/λ
ω = ω0√[1-(v2/c2)]/ [1+(v2/c2)]

ω - odbieranie, ω0 - wysłanie

1. Przestrzeń Minkowskiego: zdarzenie, interwał, rodzaje interwałów, linia świata cząstki

1. Przestrzeń Minkowskiego - czterowymiarowa przestrzeń stosowana do opisu zjawisk fizycznych w szczególnej teorii względności; trzy wymiary tej przestrzeni odpowiadają trzem wymiarom przestrzennym, a czwarty - czasowi

2. Zdarzenie można umiejscowić w czasoprzestrzeni przez podanie jego 4 współrzędnych: trzech określających położenie i czwartej - czasu

3. Interwał: Odcinek czasu. Niezmienność Interwałów:
   ds² = dx² + dy² + dz² - c²dt²
   ds² = dx² - c²dt²
   ds'² = dx'² - c²dt'² dx'= γ(dx-(v²/c²)dx)
   ds²=ds'²

4. Rodzaje Interwałów:

1. Interwał przestrzenny - nie można powiązać przyczynowo

2. Interwał zerowy - można powiać sygnałem o prędkości V=c

3. Interwał czasowy - można powiązać przyczynowo

5. Linia światła cząstki

2. Stożek świetlny - podział czasoprzestrzeni. Związek przyczynowo-skutkowy między dwoma zdarzeniami

1. Podział Czasoprzestrzeni - 4 współrzędne określające zdarzenie: 3 współrzędne przestrzenne i czas

2. Odwrócenie kolejności zdarzeń gdy nie są dwa zdarzenia powiązane przyczynowo.

3. Równoważność masy i energii - wzór Einsteina. Masa relatywistyczna

1. Równoważność masy: m = γm₀ m - masa relatywistyczna m₀ - masa spoczynkowa

2. Energia: E = mc² E - Energia całkowita E₀ = m₀c²
   Ek = E - E₀

4. Defekt masy i energia wiązania

1. Defekt masy - różnica między sumą mas poszczególnych składników układu fizycznego a masą tego układu; dla jądra atom. złożonego z Z protonów i N neutronów niedobór masy wynosi Δ(Z, N) = Zm_p + Nm_n - m (Z, N), gdzie m_p - masa protonu, m_n - masa neutronu, m(N, Z) - masa jądra; niedobór masy jest miarą energii wiązania układu

2. energia wiązania - energia, jaką trzeba dostarczyć układowi fizycznemu (np. cząsteczce, jądru atom.), aby rozdzielić go na poszczególne składniki.

5. Energia kinetyczna w STW

1. Energia: Ek = E - E₀ E = mc² E - Energia całkowita E₀ = m₀c²

2. Foton jest cząstką elementarną nieposiadającą ładunku elektrycznego ani momentu magnetycznego, o masie spoczynkowej równej zero m0 = 0, liczbie spinowej s = 1 (fotony są zatem bozonami). Fotony są nośnikami oddziaływań elektromagnetycznych i są postrzegane jako fala elektromagnetyczna.Energia fotonu E = h (h — stała Plancka,  — częstość promieniowania), pęd p = h/c

3. Masa spoczynkowa m₀ = 0

6. Efekty fizyczne przewidywane przez ogólną teorię względności

1. Odchylenie toru światła α=4GM/Rc²

2. Precesja - Obrót osi orbity planet wokół słońca

3. Grawitacyjne opóźnienie Zegarów: dτ = √(1-2GM/Rc²)dt

4. Grawitacyjny efekt Dopplera -grawitacyjne przesunięcie prążków widmowych ku czerwieni

7. Czarne dziury - promień Schwarzschilda, osobliwość, horyzont zdarzeń.

1. Czarne dziury - obiekt będący źródłem na tyle silnego pola grawitacyjnego, że niemożliwe jest przesłanie zeń na zewnątrz żadnej informacji

2. 
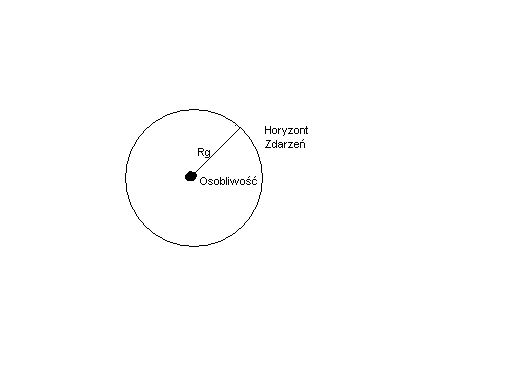
   Promień Schwarzschilda (promień grawitacyjny) - Jeśli promień grawitacyjny jest większy od promienia geometryczny, to prędkość ucieczki z powierzchni ciała przekracza prędkość światła, a zatem z ciała tego nie może wydostać się żaden rodzaj materii; ciało takie nazywa się czarną dziurą r_g = 2Gm/c²

3. Osobliwość i Horyzont zdarzeń

8. Efekty fizyczne w pobliżu czarnej dziury

1. Siły pływowe - „rozlewanie” się ciał

2. Rotacja (wleczenie)

9. Odległości w astronomii (rok świetlny)

1. Rok świetlny - jednostka długości w stosowana w astronomii. Odległość, którą światło przebiega w próżni w ciągu roku; 1 rok świetlny = 9,46 ∙ 10 ¹² km = 0,307 pc

Zasada kosmologiczna - postulat mówiący, że Wszechświat jest jednorodny i izotropowy w dużych skalach (w przestrzeni trójwymiarowej). Postulat ten ma przesłanki filozoficzne (żadne miejsce we Wszechświecie nie powinno być wyróżnione), a także obserwacyjne. Obserwacje te dotyczą zarówno izotropowości kosmicznego promieniowania tła, jak również rozkładu galaktyk w skali setek megaparseków.

Zjawisko ucieczki galaktyk polega na oddalaniu się od siebie galaktyk proporcjonalnie do odległości (im większa odległość między galaktykami tym szybciej się od siebie oddalają). Po raz pierwszy zaobserwował je Edwin Hubble w 1929 roku. Wykorzystał on fakt, iż światło niemal wszystkich galaktyk jest przesunięte ku czerwieni. Świadczy to o tym, że wszystkie galaktyki oddalają się od siebie. Swoje obserwacje opisał ilościowo tak zwanym Prawem Hubble'a.

Prawo Hubble'a jest podstawowym prawem kosmologii obserwacyjnej, wiążącym odległości galaktyk r z ich tzw. prędkościami ucieczki v (których miarą jest przesunięcie ku czerwieni z). Prawo to mówi, iż te dwie wielkości są do siebie proporcjonalne, a stałą proporcjonalności jest stała Hubble'a H0: v = H₀r

Istnienie takiej proporcjonalności zauważył (czy raczej zapostulował) jako pierwszy Edwin Hubble w roku 1929. Zależność ta jest prawdziwa dla galaktyk (ściślej: gromad) odpowiednio nam bliskich, lecz na tyle dalekich, że nie są już powiązane grawitacyjnie z Drogą Mleczną i ogólniej z Grupą Lokalną. Spełnianie przez pobliskie galaktyki prawa Hubble'a przemawia za jednorodną ekspansją Wszechświata, a odstępstwa od tego prawa są związane z tzw. prędkościami swoistymi galaktyk. W jednorodnie ekspandującym Wszechświecie, prawo Hubble'a (z odpowiednią stałą proporcjonalności, zależną od czasu kosmicznego) jest lokalnie spełnione dla wszystkich obserwatorów fundamentalnych.

Stała Hubble'a okazuje się być niestacjonarną, czyli zależna jest od wieku wszechświata. Przy płaskim modelu czasoprzestrzeni stała Hubble'a wynosi:
H(t)=2/3*t, gdzie t - wiek wszechświata.
Współczesne jej oszacowania (dane z WMAP): Ho=71 (km/s)/Mps +/-5%.

Przeszłość Wszechświata opisywana przez trzy modele kosmologiczne Friedmana wygląda podobnie. Ewolucja Wszechświata w modelu Friedmana rozpoczyna się moment zaistnienia czasu będącym początkowym stanem osobliwym, bowiem dotychczasowe teorie fizyczne nie potrafią go opisać. Moment początkowy i pierwsze chwile ekspansji określane są mianem Wielkiego Wybuchu.

Od góry: 1- otwarty ρ<ρkr, 2 - krytyczny (model Einsteina de Sittera) ρ=ρw, 3 - zamknięty ρ>ρkr. Oś Oy- czynnik skali [R(t)], Ox - czas [t]

---