IV/6 Podstawowe metody rozwiązywania ustrojów prętowych statycznie niewyznaczalnych (ms , mp)

Kinematyczna analiza konstrukcji

Geometryczna i chwilowa niezmienność - taki układ połączonych ze sobą tarcz w którym nie może nastąpić wzajemne przemieszczenie się jego części bez ich deformacji.

Stopnie swobody= 3 n = 1 s = 0 układ chwilowo chwiejny

n = 3

S = 3T - P - 2R

T - liczba tarcz → s = 3T

P - liczba prętów podporowych → s = - P

R - liczba przegubów → s = - 2R

if s = 0 - układ kinematycznie niezmienny (ma niezbędną liczbę stopni) - eliminujemy źle usytuowane

if s < 0 - układ ma więcej niż trzeba więzi do utrzymania kinematycznej niezmienności

if s > 0 - to układ jest geometrycznie zmienny

Liczba więzi nadliczbowych określana jest przez „n”

n = - s -stopień niewyznaczalności układu

n = a + p + s - 2w

a - liczba niewiadomych podporowych

p - liczba prętów

s - liczba zesztywnień

w - liczba przegubów

n = (2+1+1+1)+3+2-2•4 =

Procedura postępowania w metodzie sił

• n = ? (st. niewyznaczalności)

• przyjmujemy układ podstawowy metody sił UPMS

• zbudow. ukł. równań (model matematyczny) dla n- niewiadomych

∂₁₁x₁ + ∂₁₂x₂ + ... + ∂_1nx_n + Δ_1p = 0

∂₂₁x₁ + ∂₂₂x₂ + ... + ∂_2nx_n + Δ_2p = 0

: : : : n- równań

∂_n1x₁ + ∂_n2x₂ + ... + ∂_nnx_n + Δ_np = 0 n- niewiadomych

[∂] {X} + {ΔP} = {0}

macierz podatności wektor obciążeń

∂₁₁ ∂₁₂ ..... ∂_1n x₁ ΔP₁ 0

∂₂₁ ∂₂₂ ..... ∂_2n x₂ + ΔP₂ = 0

: : : : : :

∂_n1 ∂_n2 ..... ∂_nn x_n ΔP_n 0

• wyznaczenie M , M_p

• wyznaczenie współczynników w macierzy podatności ∂_ij , Δ_ij

• rozwiązywanie układu równań

• wyznaczenie ostatecznie M , Q , N

M⁽¹⁾_ost = M⁽ⁿ⁾₁ X₁ + M⁽ⁿ⁾₂ X₂ +...+ M⁽ⁿ⁾_n X_n + M⁽ⁿ⁾_p

• zaakceptować wyniki (sprawdzenie)

1. Σ ∫

1a. Szczególny przypadek ( kon. zamknięta)

if EJ = const

if EJ ≠ const

2. w każdym węźle ma być równowaga
   

2a. To samo dla sił

3. równowaga piętra (tam gdzie w piętrze nie ma podpór)

Schematy polowkowe

Całkowanie graficzne

UPMS

M - od siły jednostkowej

Z układu równań mamy x₁ , x₂

M_ost = M_p + M₁x₁ + M₂x₂

Ostatecznie

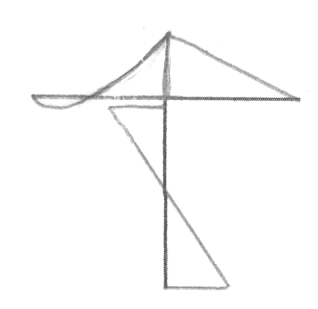
M_ost

+ sprawdzenie.

Podstawowe schematy

Wykorzystamy fakt że: symetria × antysymetria = 0

n = 9+4+3-2⋅5 = 3

Metoda przemieszczeń

Procedura

• wyznaczenie stopnia kinematycznej (i geometrycznej) niezmienności

• UPMP

• Układ równań MP

• Wyliczenie współczynnika r_ij , R_ip (czyli rozwiązanie równań i wyznaczenie ϕ i Δ)

• Wyznaczyć M]

• Wyznaczyć M_ost , N_ost M_ost = M₁ϕ₁ + M₂ϕ₂ + M_p , n_k = 2.

• Sprawdzenie wykresu M_ost

Pręt płaski

Zależność między siłami węzłowymi a przemieszczeniami

V_i v_i

φ_zi K ϕ_zi

V_k ^• v_k

φ_zk ϕ_zk

siły macierz przemieszczenia

węzłowe zależności węzłów

Macierz .................

-

-

-

-

Przykład.

IV/7

Obciążenia różnych typów; wpływ temperatury, przemieszczenia wymuszonego, uwzględnienie sprężystego podparcia punktowego i ciągłego, wykorzystanie symetrii układu i obciążeń

I. Typy obciążeń

1. Ze względu na zmianę wartości obciażenia w czasie, wyróżniamy:

Obciążenie statyczne - wartość zwiększa się powoli od zera do wartości końcowej: uznanie obciążenia za statyczne można zwiazać z najwiekszym okresem drgań własnych konstrukcji. Jeżeli czas zmiany obciążenia jest znacznie większy od największego okresu drgań własnych konstrukcji, to można to nazwać statycznym.

Obciążenie dynamiczne - wartość zmienia się nagle lub okresowo zmiennie lub w chwili przyłożenia do konstrukcji jest skończona.

2. Zależnie od czasu trwania i sposobu działania obciążenia dzieli się na:

Stałe - wartośc kierunek i położenie pozostają niezmienne w czasie użytkowania budowli, jej montażu i remontu .

Zmienne - mogą zmieniać wartość, kierunek lub położenie w czasie użytkowania budowli:

• w całości długotrwałe - np. parcie wody o stałym poziomie zwierciadła

• w części długotrwałe - np. ciężar pyłu, obciążenie od suwnic

• w całości krótkotrwałe - np. śnieg wiatr

Wyjątkowe - występują w wyniku mało prawdopodobnych zdarzeń w czasie użytkowania budowli (powódź, pożar)

II. Wpływ temperatury

Zmiana temperatury w stosunku do temp. Montażu powoduje wydłużenie pręta w osi i/lub zginanie pręta momentami powstałymi na skutek gradientu temperatur

Siły wewnętrzne powstające pod wpływem tego rodzaju obciążenia można obliczyć za pomocą metody przemieszczeń, gdzie zadane przemieszczenie więzi wynosi α * t *l (α - wsp. rozszerzalności termicznej materiału, t - temperatura, l - długość pręta) lub metodą sił w której wpływ temperatury

uwzględnia się poprzez Δ_it

równomierne ogrzanie nierównomierne ogrzanie

h - wysokość przekroju.

III. WYMUSZONE PRZEMIESZCZENIE

Siły wewnętrzne, w układzie statycznie niewyznaczalnym, wynikłe z przemieszczenia podpór wylicza się za pomocą:

• metody przemieszczeń - przemieszczenie podpór f traktuje się jako obciążenie geometryczne, stanowi osiadanie podpór lub wymuszone przemieszczenie węzłów

• metody sił - przykładowy układ równań:

gdzie:
- brak obciążeń zewnętrznych

IV. UWZGLĘDNIENIE SPRĘŻYSTEGO PODPARCIA PUNKTOWEGO I CIĄGŁEGO

Wielkością charakteryzującą podłoże sprężyste typu Winklera jest parametr k równy iloczynowi modułu podatności podłoża c i belki b.

W przypadku podparcia punktowego siły wewnętrzne można policzyć za pomocą metody sił. Rozpatrując dwa przypadki: k→ 0 i k→∝ można stworzyć obwiednie sił wewnętrznych

Podparcie ciągłe (podłoże Winklera). Podstawowe założenia:

1. Podłoże składa się z nieskończenie wielu sprężyn, a odpór odpór takiego podłoża jest wprost proporcjonalny do przemieszczenia.

2. Brak tarcia między belką a podłożem (więzy gładkie)

3. Więzy przenoszą ściskanie jak i rozciąganie

Zgodnie z powyższymi założeniami zagadnienie sprowadza się do obliczenia belki obciążonej jak na rysunku

Pod wpływem przyłożonego obciążenia punkty belki doznają przemieszczeń, które związane są z momentami zginającymi: E I w^′′(x) = -M(x). Wiedząc, że M^{′ ′}(x) = - q(x) + kw(x) równanie różniczkujemy, przekształcamy, itd. I w rezultacie otrzymujemy całkę ogólną równania w(x).

Mając dane obciążenie oraz warunki brzegowe, znamy przemieszczenia, znajdujemy funkcje momentów i sił poprzecznych. Tak rozwiązuje się belki o nieskończonej długości

Belki o skończonej długości można rozwiązać za pomocą metody Bleicha. Metodę tą stosujemy przy obliczaniu ław fundamentowych, podkładów kolejowych itp. ( Piechnik str.334 ).

V. WYKORZYSTANIE SYMETRII UKŁADU OBCIĄŻEŃ

W przypadku układów symetrycznych (np. ramy) dla ułatwienia obliczeń stosuje się tzw. schematy połówkowe, które mają mniej stopni statycznej niewyznaczalności niż układ pierwotny. Schematy obciąża się obciążeniem rozbitym na: obciążenie symetryczne i antysymetryczne. Ostateczny wykres sił wewnętrznych otrzymuje się przez zsumowanie wykresów symetrii i antysymetrii.

IV/8

Stateczność prętów prostych i płaskich ustrojów ramowych, postacie utraty stateczności, metody określania sił krytycznych.

I. Stateczność prętów prostych i płaskich ustrojów ramowych

Konstrukcja znajduje się w stanie równowagi statecznej, jeśli po dowolnie małym wychyleniu od położenia pierwotnego konstrukcja wykazuje tendencje do powrotu do tego położenia pierwotnego. Utrata stateczności prowadzi do zniszczenia konstrukcji, gdyż pociąga za sobą duże odkształcenia i to w sposób nagły

Aby konstrukcja znajdowała się w stanie równowagi statecznej muszą być spełnione warunki:

• konstrukcja musi być geometrycznie niezmienna

• obciążenie konstrukcji musi być mniejsze od krytycznego, przy którym następuje utrata stateczności

Rozważając stateczność rezygnujemy z założenia o zesztywnieniu (zmiany geometrii układu wpływają na zmianę położenia sił)

II. Postaci utraty stateczności

Postać utraty stateczności zależy od przyłożonej siły oraz od geometrii ustroju.

III. Metody określania sił krytycznych ( zakres liniowo sprężysty)

- dla prętów prostych

wzór Eulera

l_w - długość wyboczeniowa pręta

• dla płaskich ustrojów ramowych: metoda przemieszczeń

Schemat postępowania:

1. Dobór układu podstawowego MP

2. Układ równań MP

3. Wyznaczenie wsp. z_ij - nowe wzory transformacyjne dla prętów obciążonych siłą

4. Rozwiązanie układu równań

6

Podstawowe met rozw. ustrojów prętowych statycznie niewyznaczalnych (MS , MP); zał. , int. fiz. równań, dobór schem. podst.

METODA SIŁ

Stopień statycznej niewyznaczalności

r = 6 → więzy

t = 1 → liczba tarcz

p = 0

n = r + p - 3t

n = 6 + 0 - 3 ⋅ 1 = 3

Ustrój 3- krotnie statycznie niewyznaczalny

Układ podstawowy metody sił - powstaje przez usunięcie więzi

Jakie powinny być x₁ , x₂ , x₃ , aby przemieszczenie pionowe w punktach 1, 2, 3 były równe 0 ?

Stan x₁ = 1

Stan x₂ = 1

δ₁₁x₁ + δ₁₂x₂ +δ₁₃x₃ + Δ_1p = 0

Stan x₃ = 1 δ₂₁x₁ + δ₂₂x₂ +δ₂₃x₃ + Δ_2p = 0

δ₃₁x₁ + δ₃₂x₂ +δ₃₃x₃ + Δ_3p = 0

Stan p = 1

δ₁₁ δ_1n

D= macierz podatności

δ_n1 δ_nn

x₁

X= wektor niewiadomych

x₂

Δ_1p

D^F= wektor wyrazów wolnych

Δ_np

DX+D^F=0

M^h_ost = M^h₁x₁ + M^h₂x₂ + M^h₃x₃ + M^h_p

1.Wyznaczamy stopień statycznej niewyznaczalności

2.Tworzymy układ podstawowy metody sił (układ statycznie wyznaczalny- tworzymy przez usunięcie więzi nadliczbowych

3.Budujemy układ równań metody sił.Wyznaczamy współczynniki układu

4.Rozwiązujemy układ równań (wyznaczamy siły hiperstatyczne x_i)

5.Wyznaczamy rzędne ostatecznych wykresów M.,Q,N w punktach charakterystycznych

6.Sprawdzamy rozwiązanie

METODA PRZEMIESZCZEŃ

6. Metoda przemieszczeń

Procedura

*wyznaczenie stopnia kinematycznej (i geometrycznej) niezmienności układu

*UPMP

*układ równań MP (wyznaczamy współczynniki k)

*wyznaczamy M_ost

*sporządzamy wykres

8. Stateczność prętów prostych

Istota zjawiska utraty stateczności pręta prostego znana jest z kursu wytrzymałości materiałów.Występuje ono w przypadku działania na pręt siły osiowej S o tzw. wartości krytycznej S_kryt.Pręt znajduje się wówczas w stanie równowagi obojętnej; jego oś może pozostawać linią prostą,ale również nieskończenie mała dodatkowa przyczyna może wywołać jej wygięcie.Mówimy,że następuje wtedy wyboczenie pręta.Wartość krytyczną siły ściskającej dla swobodnie podpartego pręta o stałym przekroju poprzecznym wyznacza się na podstawie równania Euler'a:

w” + (SI²/EI)*w = 0

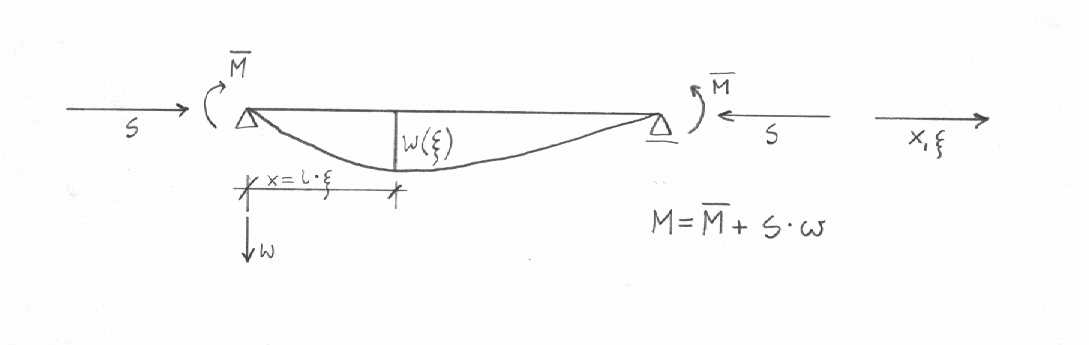
P_wyt = (Π²EI)/(μ*l²) - siła Eulerowska

Jeżeli smukłość rozważanego pręta jest większa od smukłości granicznej,to po osiągnięciu przez siłę S wartości krytycznej pręt ulega sprężystemu wyboczeniu.

Pręt ulegnie wyboczeniu przy dowolnejwartości obciążenia zewnętrznego.

W potocznym języku opór jaki stawia pręt zginany,przyjęto nazywać jego sztywnością.

Pręt rozciągany ma większą sztywność na zginanie niż pręt ściskany.

W przypadku gdy siła ściskająca ma wartość P_kr=Π²EI/(μ) sztywność pręta na zginanie jest równa 0.

Efekt polega na zmianie sztywności pręta na zginanie;ma to duże znaczenie w analizie statycznej złożonych ustrojów prętowych.

Stateczność płaskich ustrojów ramowych

K*Q=P

K-macierz sztywności

Q-wektor przmieszczeń

P-całkowity wektor obciążeń

Jeżeli założymy brak obciążeń wywołujących zginanie,wówczas wektor P=0, [K]=0

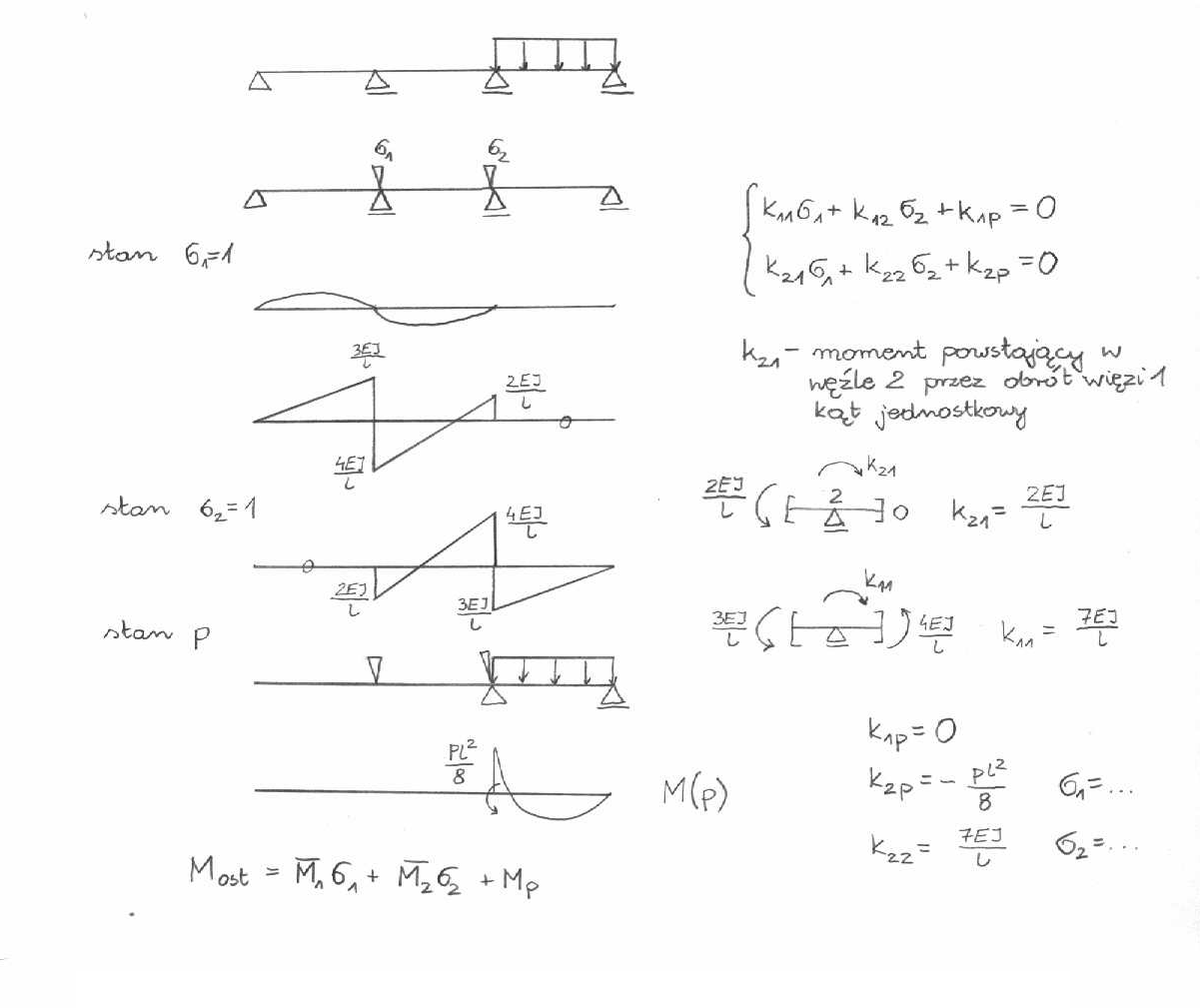
r₁₁б₁ + r₁₂Δ₂ = 0

r₂₁б₁ + r₂₂Δ₂ = 0

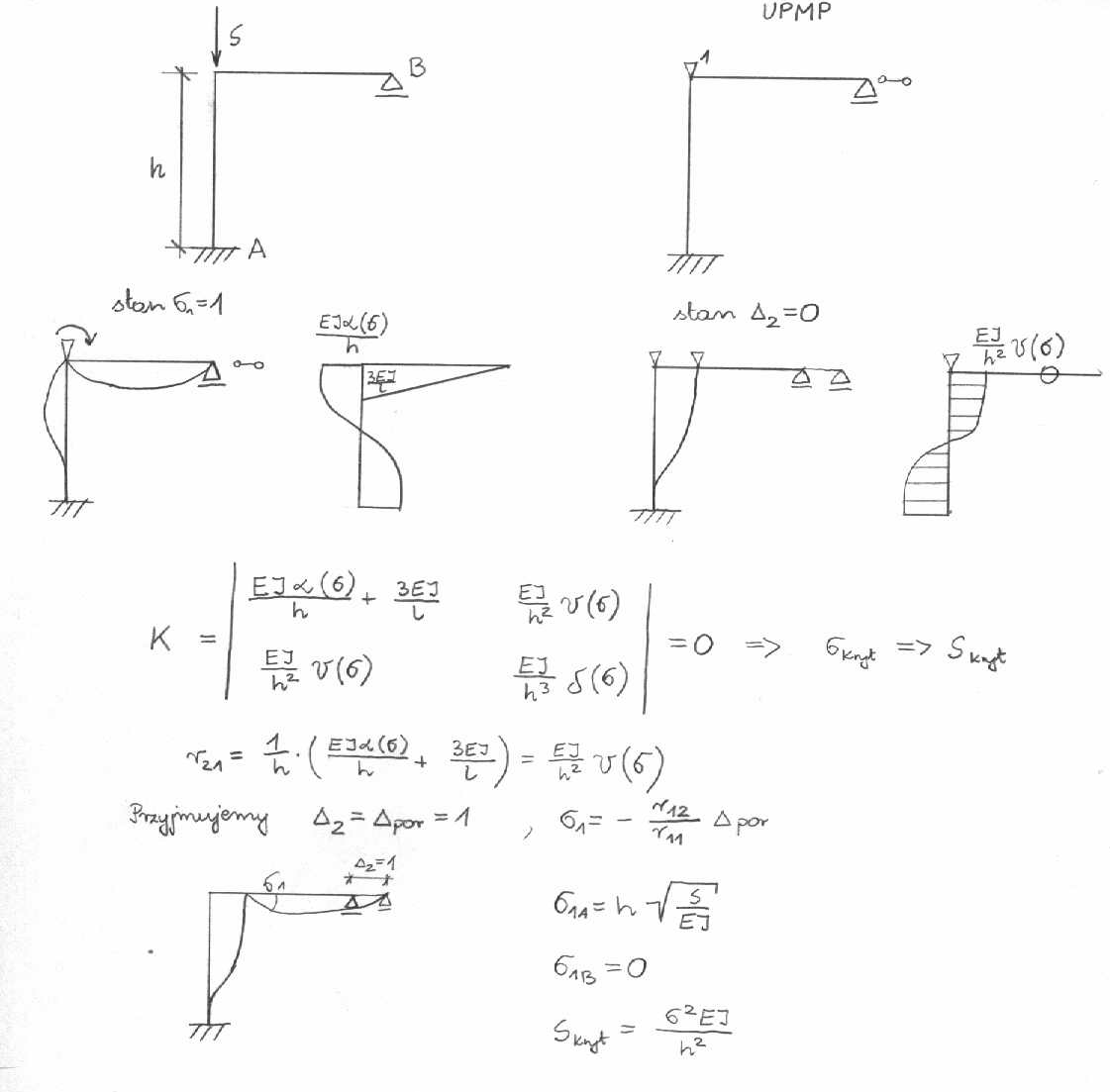
Postacie utraty stateczności

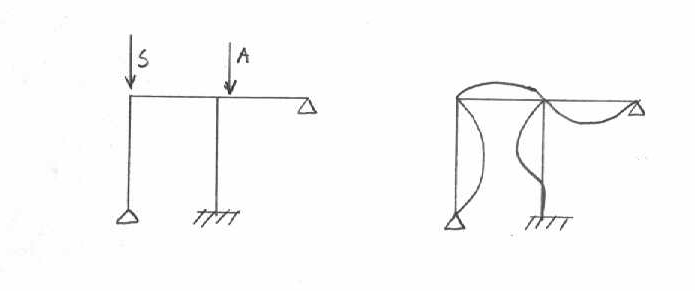
Konstrukcja znajduje się w stanie równowagi statycznej,jeśli po dowolnie małym odchyleniu od położenia pierwotnego konstrukcja wykazuje tendencje do powrotu do tego położenia pierwotnego.Utrata stateczności prowadzi do zniszczenia konstrukcji,gdyż pociąga za sobą duże odkształcenia i to w sposób nagły.

Aby konstrukcja znajdowała się w stanie równowagi statycznej muszą być spełnione warunki:

• konstrukcja musi być geometrycznie niezmienna

• obciążenie konstrukcji musi być mniejsze od P_kryt, przy którym następuje utrata stateczności

II.Postacie utraty stateczności:

Postać utraty stateczności zależy od przyłożonej siły oraz od geometrii ustroju

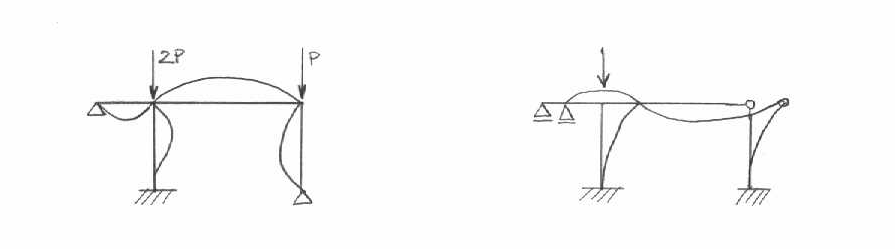
III.Metody określania sił krytycznych (zakres liniowo sprężysty)

* dla prętów prostych wzór Eulera P=Π²EI/l_w²

l_w - długość wyboczeniowa

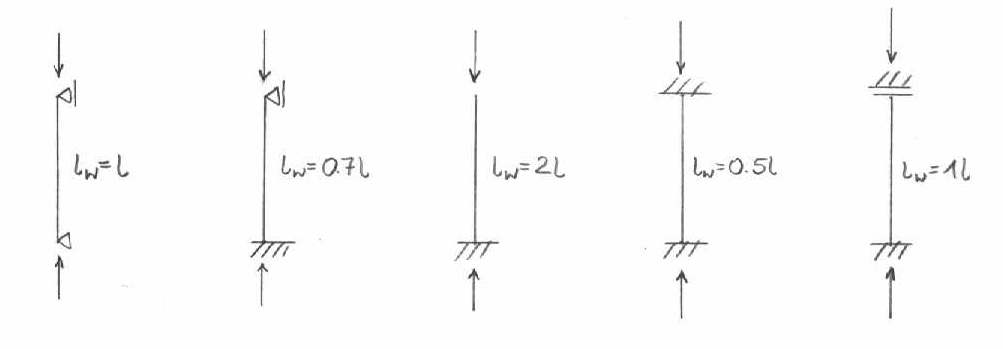
• dla płaskich ustrojów ramowych: metoda przemieszczeń

Schemat postępowania:

1.Dobór układu podstawowego MP

2.Układ równań MP

3.Wyznaczenie współczynników- nowe wzory transformacyjne dla prętów obciążonych siłą osiową

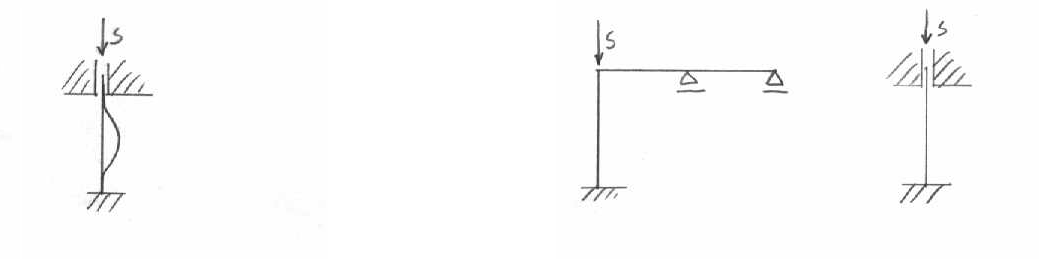
Stateczność prętów prostych i płaskich ustrojów ramowych

Stateczność

Pojedynczych prętów Układy złożone

Pręt idealny z imperfekcją idealny z imperfekcją

7. Obciążenia różnych typów; wpływ temperatury, przemieszczenia wymuszonego, uwzględnienie sprężystego podparcia punktowego i ciągłego, wykorzystanie symetrii układu i obciążeń.

I.Typy obciążeń:

• statyczne - wartość zwiększa się od zera do wartości końcowej,usuwanie obciążenia na statyczne można związać z największym okresem drgań własnych konstrukcji.Jeżeli czas zmiany obciążenia jest znacznie większy od największego okresu drgań własnych konstrukcji,to można to nazwać statycznym

• dynamiczne - wartość zmienia się nagle lub okresowo zmiennie lub w chwili przyłożenia do konstrukcji jest skończona

Zależnie od czasu trwania i sposobu działania:

• stałe - wartość,kierunek i położenie pozostają niezmienne w czasie użytkowania budowli,jej montażu i remontu

• zmienne - mogą zmieniać wartość,kierunek lub położenie w czasie użytkowania budowli

-w całości długotrwałe- np.parcie wody o stałym poziomie zwierciadła

-w części długotrwałe- np.ciężar pyłu,obciążenie od suwnic

-w całości krótkotrwałe- np.śnieg,wiatr

• wyjątkowe - występują w wyniku mało prawdopodobnych zdarzeń w czasie użytkowania budowli (powódz,pożar)

II.Wpływ temperatury

Zmiana temperatury w stosunku do temperatury montażu powoduje wydłużenie pręta w osi lub :zginanie pręta momentami powstałymi na skutek gradientu temperatur.

Siły wewnętrzne powstające pod wpływem tego rodzaju obciążenia można obliczać za pomocą metody przemieszczeń, gdzie zadane przemieszczenie wynosi α*t*l,

α- współczynnik rozszerzalności termicznej

t - temperatura

l - długość pręta

lub metodą sił, w której wpływ temperatury uwzględniony jest przez Δ_it

δ₁₁x₁ + δ₁₂x₂ + Δ_1t = 0

δ₂₁x₁ + δ₂₂x₂ + Δ_2t = 0

Δ_it = Σ [ ∫N_i*α*t_c*ds. + ∫M*α*(ΔT/h)ds. ]

h - wysokość przekroju

∫N_i*α*t_c*ds. - równomierne ogrzanie

∫M*α*(ΔT/h)ds. - nierównomierne ogrzanie

III.Wymuszone przemieszczenie

Siły wewnętrzne w układzie statycznie niewyznaczalnym,wynikłe z przemieszczenia podpór wylicza się za pomocą:

• metody przemieszczeń - przemieszczenie podpór f traktuje się jako obciążenie geometryczne stanowi osiadanie podpór lub wymuszone przemieszczenia węzłów

• metody sił - układ równań:

gdzie Δ_ip = 0 - brak obciążenia zewnętrznego

x₁δ₁₁ + x₂δ₁₂ + Δ_1p = -f

x₁δ₂₁ + x₂δ₂₂ + Δ_2p = 0

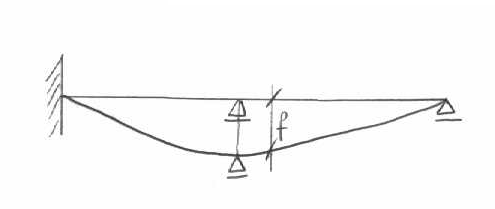
IV.Uwzględnienie sprężystego podparcia punktowego i ciągłego.

Podłoże sprężyste typu Winklera charakteryzuje parametr

k = c* b

c - moduł podatności podłoża

b - szerokość belki

np.

Podparcie ciągłe /podłoże Winklera/. Podstawowe założenia:

1.Podłoże składa się z nieskończenie wielu sprężyn,a odpór takiego podłoża jest wprost proporcjonalny do przemieszczenia

2.Brak siły tarcia między belką a podłożem /więzy gładkości/

3.Więzy przenoszą zarówno ściskanie jak i rozciąganie

Zgodnie z zał. zagadnienie sprowadza się do obliczenia belki obciążonej jak na rys.

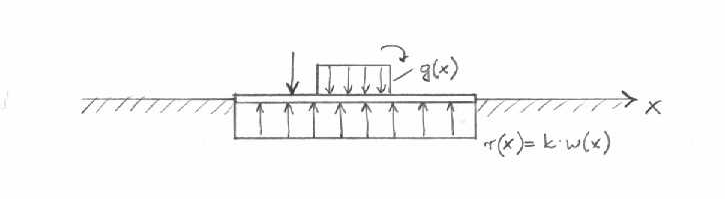
Pod wpływem przyłożonego obciążenia punkty belki doznają przemieszczeń,które związane są z momentami zginającymi EI*w''(x) = -M.(x)

Wiedząc,że M.''(x) = -q(x) + k*w(x) równanie różniczkujemy, przekształcamy itd. i w rezultacie otrzymujemy równania na w(x).

Mając dane obciążenie oraz warunki brzegowe, znamy przemieszczenia,znajdujemy funkcję momentów i sił poprzecznych.Tak rozwiązuje się belki o nieskończonej długości.

V.Wykorzystanie symetrii układu

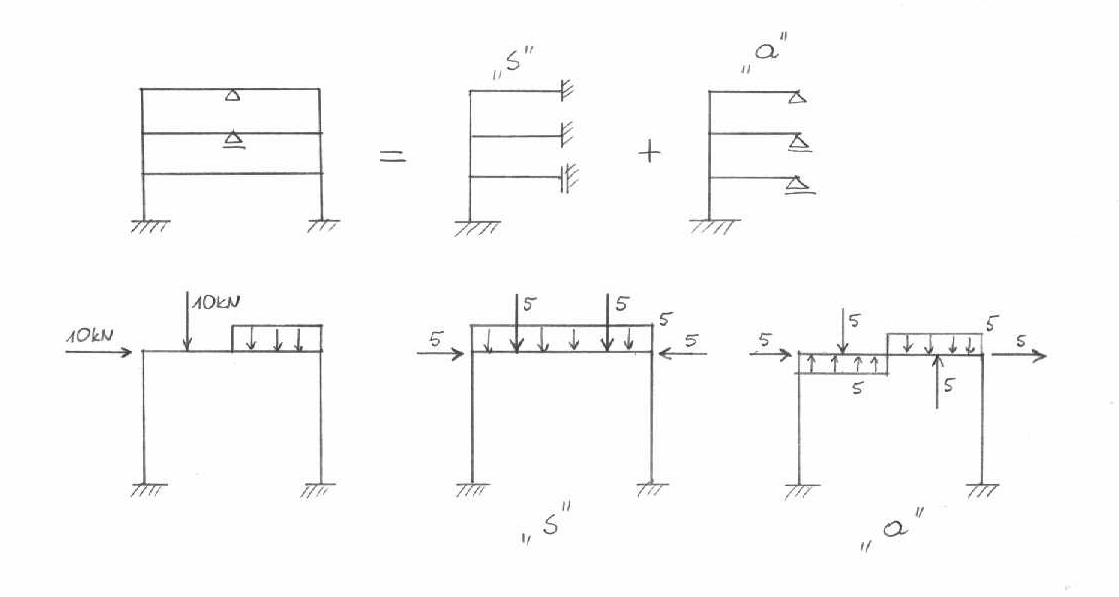
W przypadku układów symetrycznych stosuje się schematy połówkowe,które mają mniej stopni statycznej niewyznaczalności niż układ pierwotny.Schematy połówkowe obciąża się obciążeniem rozbitym na: obciążenie symetryczne i antysymetryczne .Ostateczny wykres sił wewnętrznych otrzymuje się przez zsumowanie wykresów z symetrii i antysymetrii.

---