ANNA POŁOWNIAK

FM2R2

Zespół 13

SPRAWOZDANIE Z LABORATORIUM 5.10.2008

Ćw. Nr 1: WAHADŁO FIZYCZNE

Wstęp:

Wahadło fizyczne.

Dowolne ciało sztywne zawieszone tak, że może się wahać dookoła pewnej osi przechodzącej przez to ciało, nazywamy wahadłem fizycznym. Wahadło proste, gdzie na nieważkiej nici zawieszony jest pojedynczy punkt materialny, jest szczególnym przypadkiem wahadła fizycznego. W rzeczywistości wszystkie realne wahadła są wahadłami fizycznymi.

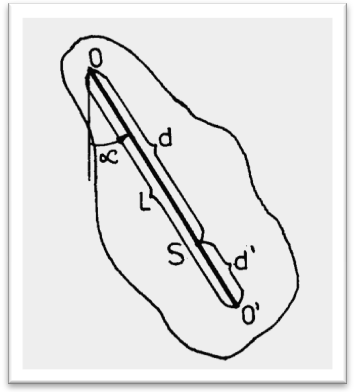
Rysunek przedstawia ciało o nieregularnym kształcie, które może się obracać dookoła poziomej osi przechodzącej przez punkt O , bez tarcia. Zostało ono odchylone od położenia równowagi o kąt α. Położenie równowagi, to takie położenie w którym środek masy ciała S leży w linii pionowej przechodzącej przez punkt O. Odległość między osią obrotu przechodzącą przez punkt O, a środkiem masy S oznaczamy przez d, a moment bezwładności względem osi obrotu przez I.

Wahadło odchylone od pionu o kąt α, a następnie swobodnie puszczone będzie wykonywać drgania zwane ruchem wahadłowym. W ruchu tym mamy do czynienia z obrotem bryły sztywnej wokół osi, co opisuje druga zasada dynamiki dla ruchu obrotowego:

M= I∙ε ,

M- moment siły

I - moment bezwładności

ε- przyspieszenie kątowe ( wiemy, że ε=
)

Dla wahadła moment siły M powstaje pod wpływem siły ciężkości. Dla wychylenia α jest on równy:

M= mgdsinα (d- odległość środka ciężkości S od osi obrotu O)

Równanie ruchu wahadła możemy zapisać jako:

Minus po prawej stronie uwzględnia, że moment siły jest skierowany przeciwnie do kierunku wychylenia.

Jeżeli ograniczymy ruch do małych kątów, to sinus kąta możemy zastąpić samym kątem w mierze łukowej (sinα
α ). Przy tym założeniu równanie ruchu przyjmuje postać:

+
α= 0 (gdzie
).

Okres drgań wahadła:

T=2π

1.Cel ćwiczenia:

-zapoznanie się z ruchem drgającym wahadła fizycznego,

-wyznaczenie momentu bezwładności brył sztywnych, przez pomiar ich okresu drgań,

-opis ruchu wahadła.

2. Przebieg ćwiczenia:

Po otrzymaniu przyrządów dodatkowych: w tym wypadku suwmiarki i stopera, skorzystaliśmy z przygotowanego układu pomiarowego, który składał się ze statywu, wagi, przymiaru liniowego, pręta i pierścienia.

Dokonaliśmy pomiaru masy, długości i odległości osi obrotu od środka ciężkości obu badanych przedmiotów, a także określiliśmy niepewność standardową dla pomiarów.

	Pomiar masy i długości
	Pręt			Pierścień
	masa [kg]	l [m]	a [m]	masa [kg]	Rw [m]	Rz [m]	a [m]
Wartość	0,665	0,746	0,275	1,362	0,125	0,14	0,109
Niepewność standardowa	0,001	0,001	0,001	0,001	0,001	0,001	0,001

Następnie dokonaliśmy wychylenia wahadła (najpierw w postaci pręta, później w postaci pierścienia) o kilka stopni (ok. 5) i mierzyliśmy czas kilkudziesięciu drgań (od 25 do 29), dla każdej wartości k (drgań) pomiar przeprowadzaliśmy dwukrotnie.

Wyniki pomiarów:

Pomiar czasu drgań dla pręta
Lp.	Liczba drgań k	Czas drgań t [s]	Okres drgań Ti [s]	Wartość średnia okresu Tśr [s]	niepewność standardowa u(T) [s]
1	25	33,18	1,3272
2	25	33,43	1,3372
3	26	34,81	1,338846154
4	26	34,96	1,344615385
5	27	35,84	1,327407407	1,330423857	0,008271403
6	27	35,82	1,326666667
7	28	37,1	1,325
8	28	37,29	1,331785714
9	29	38,58	1,330344828
10	29	38,14	1,315172414

Pomiar czasu drgań dla pierścienia
Lp.	Liczba drgań k	Czas drgań t [s]	Okres drgań Ti [s]	Wartość średnia okresu Tśr [s]	niepewność standardowa u(T) [s]
1	25	25,59	1,0236
2	25	25,81	1,0324
3	26	26,7	1,026923077
4	26	26,72	1,027692308
5	27	27,59	1,021851852	1,023164896	0,006513925
6	27	27,48	1,017777778
7	28	28,37	1,013214286
8	28	28,49	1,0175
9	29	29,54	1,01862069
10	29	29,93	1,032068966

Niepewność standardową wyliczamy ze wzoru:

u(T)=

gdzie n określa, liczbę wykonanych pomiarów.

Wyniki niepewności zaokrąglam do 0,001, ponieważ taką niepewność standartową pomiaru uzyskałam przy mierzeniu długości, masy i odległości osi obrotu od środka ciężkości pręta i pierścienia:

u(T)= 0,008 - dla pręta,

u(T)= 0,007 - dla pierścienia.

3.Opracowanie wyników pomiarów:

*Obliczam korzystając ze wzoru:

T=

Moment bezwładności dla pręta i pierścienia względem osi obrotu .

T=

- dla pręta:
0,081

-dla pierścienia:
=0,039

*Korzystając z twierdzenia Steinera obliczam moment bezwładności względem osi przechodzącej przez środek masy:

-

-dla pręta: 0,031

-dla pierścienia: 0,023

*Obliczam moment bezwładności względem osi przechodzącej przez środek masy znając masę i odpowiednie wymiary geometryczne:

-dla pręta:

0,030

-dla pierścienia:

Dla pręta:

	I0 wyznaczone z okresu drgań [ kg * m^2 ]	IS wyznaczone z twierdzenia Steinera [ kg * m^2 ]	IS wyznaczone z pomiarów geometrycznych [ kg * m^2 ]
Wartość	0,081	0,031	0,030
Niepewności	0,001	0,001	0,001

Dla pierścienia:

	Io wyznaczone z okresu drgań [ kg * m^2 ]	IS wyznaczone z twierdzenia Steinera [ kg * m^2 ]	IS wyznaczone z pomiarów geometrycznych [ kg * m^2 ]
Wartość	0,039	0,023	0,023
Niepewności	0,001	0,001	0,001

*niepewność złożona momentu bezwładności względem osi przechodzącej przez środek masy (znając masę i wymiary geometryczne przedmiotów):

- dla pręta:

u(
=

u(
=

u(
= 0,0003

-dla pierścienia:

u(
=

u(
=

u(
= 0,0007

u(m)=0,001- niepewność pomiaru masy;

u(l)=0,03- niepewność pomiaru długości l;

u(R)=0,003- niepewność pomiaru promienia R;

*Porównuję otrzymane wartości momentów bezwładności względem osi przechodzących przez środek masy (wyliczone z twierdzenia Steinera i ze znajomości masy oraz wartości geometrycznych obiektów)

W przypadku pręta mamy do czynienia z wartościami rzędu: 0,031 i 0,030 a w przypadku pierścienia: 0,023 i 0,023 . Wartości te są do siebie w jednym przypadku bardzo zbliżone a w drugim identyczne.

4.Wnioski z doświadczenia:

- zbliżone/identyczne wartości momentów bezwładności przechodzących przez środek masy świadczą o prawdziwości pomiarów geometrycznych;

- zbliżone wartości mierzonych wartości świadczą o rzetelności i dokładności wykonywanych pomiarów;

- w zależności od kąta okres drgań wahadła ulegał zmianie;

-Im dokładniejsze wyniki pomiarów tym dokładniejszy moment bezwładności z twierdzenia Steinera i z pomiarów geometrycznych i tym mniejsze niepewności standardowe.

---