Zagadnienia teoretyczne:

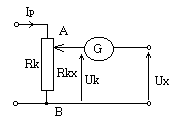
Pomiar metodą kompensacyjną polega na zrównoważeniu wartości mierzonej wartością znaną. Porównywalne są ze sobą dwa napięcia lub siła elektromotoryczna z napięciem. Zasadę pomiaru przedstawiono na rys. Napięciu mierzonemu Ux przeciwstawiony jest spadek napięcia między punktami AB. Napięcie to można regulować i wyznaczyć jego wartość. W chwili zrównania się napięcia Uk z napięciem Ux galwanometr wskaże wychylenie równe zero. Układ jest wtedy w stanie kompensacji i nie pobiera prądu z obiektu mierzonego. Jest to ważna zaleta metody kompensacyjnej. Napięcie Ux można skompensować napięciem Uk dwoma sposobami:

1. regulując prąd Ip przy zachowaniu stałej rezystancji Rkx;

2. zmieniając rezystancję Rkx przy zachowaniu stałej wartości prądu Ip.

Przebieg ćwiczenia:

1. Schemat układu do wyznaczenia charakterystyki obciążenia (prądowo-napięciowej) zasilacza stabilizowanego napięciowo o Uz = 5 V. Prąd 2 A.

2. Pomiary charakterystyki obciążenia (prąd.-nap.) zasilacza, zmieniając prąd rezystorem nastawnym w zakresie od 50 do 150 działek.

[mA]	50.0	60.0	70.0	80.0	90.0	100.0	110.0	120.0	130.0	140.0	150.0
[V]	4.987	4.984	4.980	4.977	4.973	4.970	4.966	4.962	4.958	4.955	4.950




3. Obliczenie rezystancji wewnętrznej Rw źródła dla I1 = 500.0mA i I2 = 1500.0mA i odpowiednio U1 i U2 oraz niepewność względną <δRw> i bezwzględną <ΔRw> rezystancji wewnętrznej.

U2=4.950 V U1=4.987 V I2=1500.0 mA I1=500.0 mA




<ΔU1>=0.05%·4.987+0.003=5.494·10^-3V

<ΔU2>=0.05%·4.950+0.003=5.475·10^-3V

<δU1>=1.102·10^-3

<δU2>=1.106·10^-3

<ΔI1>=0.2%·1.5=0.003A

<ΔI2>=0.2%·1.5=0.003A

<δI1>=0.006

<δI2>=0.002







<δ(U2-U1)> = 0.209

<δ(I2-I1)> = 0.009

<δ(Rw)> = |0.209|+|0.009| = 0.218

<ΔRw> = 0.008 Ω

Rw = (0.037±0.008)Ω

4. Metoda częściowej kompensacji.




[mA]	50.0	150.0
[mV]	96.7	60.9

U2=96.7 mV U1=60.9 mV I2=1500.0 mA I1=500.0 mA




<ΔU1>=0.05%·60.9+0.03=60.45·10^-3 mV

<ΔU2>=0.05%·96.7+0.03=78.35·10^-3mV

<δU1>=0.993·10^-3

<δU2>=0.810·10^-3

<ΔI1>=0.2%·1.5=0.003A

<ΔI2>=0.2%·1.5=0.003A

<δI1>=0.006

<δI2>=0.002







<δ(U2-U1)> = 3.015·10^-3

<δ(I2-I1)> = 0.009

<δ(Rw)> = |3.015·10^-3|+|0.009| = 12.015·10^-3

<ΔRw> = 0.430mΩ

Rw = (35.8±0.4)mΩ

Wnioski:

Przez zastosowanie metody częściowej kompensacji zwiększyliśmy dokładność pomiaru.




---