WMS	Imię i nazwisko: Bożena Skrzypek Tomasz Sumara			Zespół: 3	Grupa: Środa 14.45	Rok III
Nr ćwiczenia: 1	Temat: Wahadło fizyczne
Data wykonania: 14.10.09	Data oddania: 21.10.09	Zwrot do poprawy:	Data oddania:		Data zaliczenia:	Ocena:

1. CEL ĆWICZENIA:

Zapoznanie się z ruchem drgającym wahadła fizycznego oraz wyznaczenie momentu bezwładności pręta i pierścienia przez pomiar okresu drgań wahadła fizycznego.

2. WPROWADZENIE:

Wahadło matematyczne - punkt materialny zawieszony na nieważkiej i nierozciągliwej nici

Wahadło fizyczne - bryła sztywna, mogąca obracać się wokół osi obrotu nie przechodzącej przez środek masy

Wahadło fizyczne odchylone od pionu i puszczone swobodnie porusza się ruchem drgającym. Jest to ruch obrotowy wokół osi O pod wpływem momentu siły, powodowanego przez siłę ciężkości. Dla wychylenia θ moment siły jest równy:

Dla małych wychyleń, wartość
można przybliżać przez
, czyli:

Z kolei z II zasady dynamiki dla ruchu obrotowego:

Stąd:

Niech
, wtedy po rozwiązaniu równania różniczkowego:

Okres drgań wyliczamy z zależności:

Porównując oba równania otrzymujemy:

Czyli:

Zatem moment bezwładności możemy wyliczyć ze wzoru:

Aby obliczyć moment bezwładności względem osi przechodzącej przez środek masy, należy skorzystać z twierdzenia Steinera:

Moment bezwładności bryły sztywnej wyraża się jako całka oznaczona:

Dla pręta wynosi on:

Dla pierścienia:

3. UKŁAD POMIAROWY:

Statyw, stoper, waga, suwmiarka, przymiar liniowy, pręt, pierścień

4. OPIS ĆWICZENIA:

1. Pomiar masy pręta i pierścienia

2. Pomiar długości (l) pręta oraz promieni: wewnętrznego (R_w) i zewnętrznego (R_z) pierścienia

3. Pomiar odległości środka masy od osi obrotu (a)

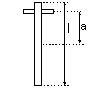
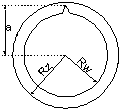
4. Wprowadzenie ciał w ruch drgający o nieznacznej amplitudzie i pomiar czasu 30 drgań (pomiar powtarzany 10-krotnie)

5. Obliczenie wartości średnich oraz niepewności standardowych według wzoru:

, gdzie n oznacza liczbę wykonanych pomiarów (10).

5. WYNIKI POMIARÓW:

Tabela 1: Pomiary masy i długości

	Pręt			Pierścień
	masa [kg]	I [m]	a [m]	masa [kg]	Rw [m]	Rz [m]	a [m]
wartość	0,665	0,75	0,275	1,346	0,125	0,14	0,129
niepewność standardowa

Tabela 2: Pomiary czasu drgań dla pręta:

Lp i	Liczba drgań k	Czas drgań t [s]	Okres drgań Ti [s]	Wartość średnia okresu T [s]	Niepewność standardowa u(T) [s]
1.	30	40,35	1,34500	1,3327	0,0016
2.	30	39,88	1,32933
3.	30	39,94	1,33133
4.	30	40,03	1,33433
5.	30	39,95	1,33167
6.	30	39,94	1,33133
7.	30	39,93	1,33100
8.	30	40,09	1,33633
9.	30	39,87	1,32900
10.	30	39,84	1,32800

Tabela 3: Pomiary czasu drgań dla pręta:

Lp i	Liczba drgań k	Czas drgań t [s]	Okres drgań Ti [s]	Wartość średnia okresu T [s]	Niepewność standardowa u(T) [s]
1.	30	30,93	1,03100	1,02760	0,00087
2.	30	31	1,03333
3.	30	30,79	1,02633
4.	30	30,75	1,02500
5.	30	30,81	1,02700
6.	30	30,75	1,02500
7.	30	30,81	1,02700
8.	30	30,78	1,02600
9.	30	30,88	1,02933
10.	30	30,78	1,02600

6. OPRACOWANIE WYNIKÓW POMIARÓW:

1. Moment bezwładności względem osi obrotu wyznaczyliśmy ze wzoru:

, gdzie T jest wartością średniego okresu .

2. W celu wyznaczenia momentu bezwładności względem osi przechodzącej przez środek masy I_s skorzystaliśmy ze wzoru Steinera:
   

3. Moment bezwładności względem osi przechodzącej przez środek masy obliczyliśmy na podstawie pomiarów geometrycznych ze wzorów odpowiednio dla pręta i pierścienia:

Niepewności złożone obliczyliśmy na podstawie wzoru ogólnego:

Ad.1)

Ad.2)

Ad.3)

Dla pręta:

Dla pierścienia:

Wyniki zamieszczone są w tabelach poniżej:

Tabela 4: Wyniki obliczeń momentów bezwładności dla pręta:

	I0 wyznaczone z okresu drgań	IS wyznaczone z twierdzenia Steinera	IS wyznaczone z pomiarów geometrycznych
Wartość		0,368127045	0,031171875
Niepewność standardowa

Tabela 5: Wyniki obliczeń momentów bezwładności dla pierścienia:

	I0 wyznaczone z okresu drgań	IS wyznaczone z twierdzenia Steinera	IS wyznaczone z pomiarów geometrycznych
Wartość		0,0231621844	0,023706425
Niepewność standardowa

2. WNIOSKI
   

Skopiowane z innych sprawozdań: (nie myślałam jeszcze nad tym, bo nie obliczyłam tego wszystkiego…czekam aż sprawdzisz, czy dobrze pochodne itp..:P!)

Źródłem błędów był opór ośrodka, w którym poruszało się wahadło oraz niedokładność przy włączaniu i wyłączaniu stopera przez osobę prowadzącą doświadczenie.

Porównując ze sobą wartości I_{s obl.} i I_s wyznaczone z twierdzenia Steinera

zauważamy, że różnią się między sobą. Różnica ta spowodowana jest

niedokładnością pomiaru co wykazaliśmy w punkcie pt. Błędy.

Rozpatrując błędy dla obydwóch prętów widzimy, że na wartość końcowego błędu wyliczonego z prawa przenoszenia błędów największy wpływ ma pomiar odległości „a” i masy „m”. Natomiast przy badaniu obu pierścieni największy wpływ na wartość błędu końcowego miał pomiar odległości „a” i okresu „T”.

Przy dokładnym pomiarze momentu bezwładności dla tych ciał należałoby zwrócić szczególną uwagę na dokładniejszy pomiar tych wartości, które wprowadzają największy błąd.

Metoda pomiaru momentu bezwładności za pomocą wahadła fizycznego okazała się niebywale dokładna, gdyż w małym stopniu odbiegała od wyników uzyskanych na podstawie pomiarów geometrycznych.

Zaobserwowaliśmy, że gdy zwiększymy ilość wahnięć wahadła to okres w mniejszym stopniu odbiega od wartości średniej.

Źródłem błędów był niewątpliwie opór ośrodka, w którym poruszało się wahadło. Opór tegoż ośrodka nie był założony w rozważaniach teoretycznych.

Strona 5 z 6

---