Ruch drgający

1. Drgania tłumione

2. Drgania swobodne

3. Przemiany energii w ruchu drgającym

4. Składanie drgań

5. Drgania wymuszone. Zjawisko rezonansu

Drgania tłumione

Z II zasady dynamiki:

równanie drgań tłumionych

rozwiązanie równania drgań tłumionych

gdzie:

A₀ - amplituda początkowa drgań

ၪ  początkowa faza drgań

ၷ  pulsacja drgań tłumionych

Jeśli = 0, to w chwili t = 0 mamy x = A₀

ၷ ma sens fizyczny, jeśli

Dekrement tłumienia:

gdzie:

δ  logarytmiczny dekrement tłumienia

stąd

metoda wyznaczania współczynnika tłumienia ၤ

b gliceryny = 13,9

b wody = 0,01

Czasem relaksacji ၴ nazywamy czas, po którym amplituda drgań zmaleje e-krotnie.

Czas relaksacji jest wprost proporcjonalny do masy ciała drgającego i odwrotnie proporcjonalny do współczynnika tłumienia.

Drgania swobodne

równanie drgań swobodnych

rozwiązanie równania drgań swobodnych

gdzie:

 pulsacja drgań swobodnych,

- maksymalne wychylenie ciała z położenia równowagi (amplituda

drgań, stała w czasie)

gdzie:

T - okres drgań swobodnych

Częstość drgań swobodnych

Związek między pulsacją drgań swobodnych i częstością:

Przemiany energii w ruchu drgającym

x = 0, to
,

x =
, to
,

Dla małych kątów ၪ ruch wahadła jest ruchem harmonicznym.

Okres wahań nie zależy od amplitudy - wahania są izochroniczne.

Przyśpieszenie w ruchu harmonicznym jest proporcjonalne do wychylenia x.

Składanie drgań

Drgania wzajemnie prostopadłe

Punkt A' wykonuje jednocześnie dwa drgania harmoniczne:

wzdłuż osi X

wzdłuż osi Y

Przypadek I

Przypadek II

Ruch wypadkowy punktu odbywa się po elipsie, której półosie równają się odpowiednio A i B.

Przypadek III

Ruch punktu B' można uważać za wynik złożenia dwóch ruchów harmonicznych o jednakowej amplitudzie i przesuniętych w fazie o
.

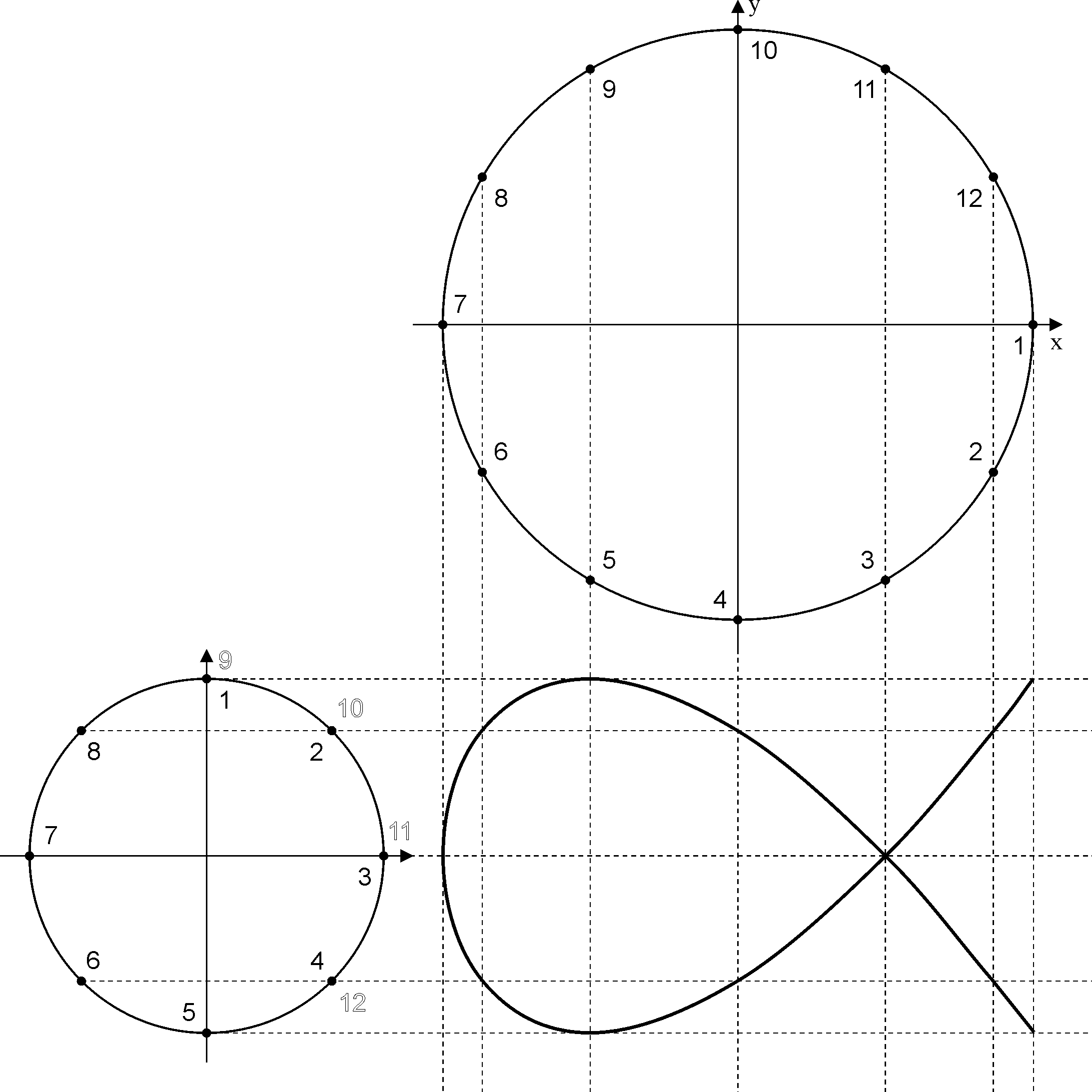
Krzywe Lissajous

Superpozycja drgań harmonicznych wzdłuż jednej prostej

Wprowadzamy pojęcie wektora amplitudy . Jest to wektor o długości A, wirujący z prędkością kątową ၷ, przeciwnie do ruchu wskazówek zegara. Rzut wektora amplitudy na oś OX zmienia się zgodnie z zależnością charakteryzującą drgania harmoniczne: .

Przykład 1

Cząstka uczestniczy równocześnie w dwóch drganiach harmonicznych o jednakowych pulsacjach
, amplitudach A₁ i A₂ oraz fazach
i
, zachodzących wzdłuż osi OX:

Kąt między wirującymi wektorami i jest stały w czasie:

Oznacza to, że wektor
również wiruje z prędkością kątową ၷ, a jego rzut na oś OX jest równy:

Obliczamy amplitudę drgania wypadkowego A oraz fazę początkową ϕ.

Rozważmy
. Kąt przy wierzchołku B wynosi
.

Bok OB = A₁, BC = A₂, OC = A.

Z twierdzenia cosinusów:

Z równania * wynika, iż amplituda drgania wypadkowego zależy od różnicy faz
.

Obliczamy fazę ϕ drgania wypadkowego:

Zatem:

Przypadek 2

Cząstka uczestniczy w dwóch drganiach harmonicznych o różnych pulsacjach
. Fazy początkowe
. Zatem:

Kąt między wirującymi wektorami
i
wynosi:

a więc zmienia się w czasie. Wypadkowy wektor amplitudy
ma zmienną w czasie długość (A zależy od czasu).

Rozważmy przypadek:
oraz
bardzo małe. Zatem:

ale
. Otrzymujemy:

Drganie wypadkowe można traktować (w przybliżeniu) jako harmoniczne o pulsacji ω i amplitudzie wolno zmieniającej się w czasie. W takim przypadku mówimy o dudnieniach, ω nazywamy pulsacją dudnień.

Amplituda drgania wypadkowego jest równa zero w momentach:

Dudnienia obserwujemy przy składaniu drgań o mało różniących się częstościach.

Drgania wymuszone. Zjawisko rezonansu.

Na punkt materialny wykonujący drgania tłumione wzdłuż osi X (a więc poddany działaniu siły sprężystości
i siły oporu
) działa siła zewnętrzna, zmienna w czasie
(
 amplituda siły,
 pulsacja siły wymuszającej drgania).

Z II zasady dynamiki:

równanie drgań wymuszonych

Rozwiązaniem tego równania jest wyrażenie:

Oznacza to, że pod wpływem siły wymuszającej drgania, ciało drga z pulsacją równą pulsacji siły wymuszającej drgania. Różnica faz wynosi Φ, zaś amplituda drgań określona jest wzorem:

Amplituda A zależy od pulsacji siły wymuszającej drgania.

Różnicę faz  możemy wyznaczyć ze wzoru:

Obliczmy z jaką pulsacją Ω powinna zmieniać się siła F, by amplituda osiągnęła wartość maksymalną, tzw. amplitudę rezonansową
. Badamy ekstremum funkcji pod pierwiastkiem.

Obliczmy amplitudę rezonansową.

Rodzaj drgań	Siły działające	Równanie ruchu	Rozwiązanie równania ruchu
Drgania swobodne
Drgania tłumione
Drgania wymuszone

Ruch drgający • Fizyka 2002 - 2003

2

---