EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH - WYKŁADY
Wykład z dnia 17.05.2014 r.
Analityczne wyrównanie
Do drugiej grupy należą metody pod ogólną nazwą analitycznego wygładzania. W podstawie tych metod leży hipoteza, że badamy szereg czasowy y1 , y2, … , yn . Ma pełną regułę czyli trend , który można określić pełną funkcją : yt = f(t).
Odnotujemy, że czas ten jest tutaj rozpatrywany jak niezależna zmienna a poziomy szeregu czasowego yi , i = 1,2, …,n są funkcjami tej niezależnej zmiennej. Przy tym w badaniach ekonomicznych uważa się niewykorzystanie dla określenia trendu funkcji z wielką ilością parametrów (wielomian dużego rzędu). Takie funkcje będą określać losowe drgania a nie podstawowe tendencje szeregu czasowego. Przy konstrukcji i modeli prognozy na podstawie yt = f(t) uważa się, że poziomy szeregów czasowych odzwierciedli oddziaływanie wielu czynników na socjalną ekonomiczną procesu. Ekstrapolacja yt = f(t) daje możliwość dostać wartość prognozy w konkretnym punkcie tzn. otrzymać punktowy progres. Takie oszacowanie jest szeregiem oszacowania dla prognozowania okresu tak jak faktyczny poziom szeregu czasowego. Prawie nigdy nie są te same co teoretyczne czy normatywne wartości
![]()
Określone na podstawie modeli prognozy to warto też określić przedziały ufności prognozy.
Takie przedziały są określone wzorem :
![]()
gdzie:
![]()
- teoretyczna wartość prognozowanej
![]()
- współczynnik prawdopodobieństwa obliczany przy danej wartości α i danej liczby
stopniu wolności (=2) z tablicami t - rozkładu czy tablicami Studenta
n - objętość szeregu czasowego
α - przedział prognozowanej
n + α - średnie kwadratowe odchylenie trendu
Będziemy rozpatrywać najprostsze konstrukcje trendu na podstawie ekstrapolacji liniowej i parabolicznej funkcji.
W jednym z najprostszych podejść do konstrukcji trendu jest metoda najmniejszych kwadratów.
Szereg czasowy
Y1 , Y2 , … , Yn (1)
Yn - objętość szeregu czasowego
Przypuszczamy, że poziomy szeregu czasowego są dane w jednakowych okresach czasu.
ti - ti-1 = tj - tj-1
Przypuszczamy dalej, że podstawowa tendencja dynamiki dość dobrze jest opisana przez pewien wielomian p -tego rzędu.
![]()
(2)
ai - parametry wielomianu
t2 - czas
Na podstawie metody najmniejszych kwadratów niewiadome parametrów są otrzymywane na podstawie:
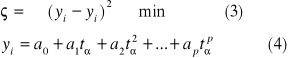
![]()
Podstawiając równanie 4 pod 3 otrzymujemy :
![]()
Z matematyki wiadomo, że funkcja z wieloma zmiennymi 5 będzie przyjmować wartości minimalne w tych punktach w których pochodne cząstkowe po odpowiednich parametrach są równe zero, tzn. że niewiadome parametry a0 , a1 , a2 są rozwiązaniem niewiadomego układu równań:
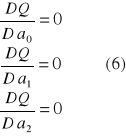
![]()
Po wykonaniu operacji różniczkowania otrzymujemy :
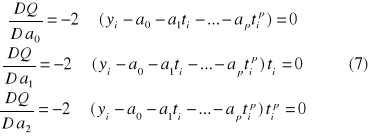
![]()
Po prostej transformacji w układzie 7 otrzymujemy :
![]()
![]()
} (8)
![]()
Układy równań 8 nazywa się normalnym układem równań dla znalezienia niewiadomych parametrów a0 , a1 , a2.
Rozpatrzymy wypadki szczególnych układów normalnych (8).
p = 1
tzn. że tendencja trendu ma postać liniową
![]()
Dla znalezienia niewiadomych parametrów a0 , a1 wypisujemy normalny układ dwóch równań z dwiema niewiadomymi.
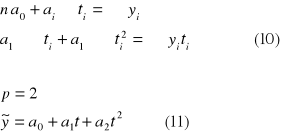
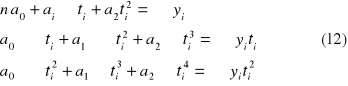
Układy równań 10 i 12 można istotnie uprościć jeśli zamiast zwykłego czasu ti wziąć uogólniony czas ![]()
, który powinien spełnić warunki:
![]()
Tzn. że sumy uogólnionych czasów z nieparzystymi potęgami powinny być równe zero. Na podstawie tej zamiany zamiast układu 9, 10 otrzymujemy :
![]()
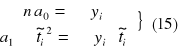
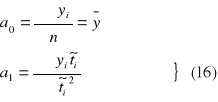
Na podstawie tej samej zamiany wypisujemy otrzymany układ
![]()
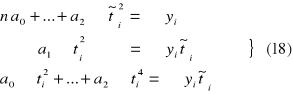
Rozpatrzymy teraz interpretację ekonomiczną parametru trendu.
Wartość parametru trendu a1 , przedstawia szybkość zmiany podstawionej tendencji dynamiki czyli szybkości zmiany trendu.
Wartość parametru trendu a2 przedstawia przyśpieszenie zmiany podstawionej tendencji dynamiki czyli przyśpieszenia zmiany trendu.
Dla wartości parametru trendu a0 nie ma żadnej interpretacji ekonomicznej. Podobno nie ma interpretacji dla parametru a3 , a4 itd.
1. Oceny prognozy przedstawione na podstawie liniowej metody trendu
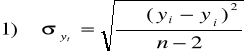
2. Oceny prognozy przedstawione na podstawie
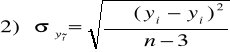
![]()
Wyszukiwarka
Podobne podstrony:
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 22.03.2014, IV rok, Wykłady, Ekonometria i progno
EKONOMIA MATEMATYCZNA 23.03.2014, IV rok, Wykłady, Ekonomia matematyczna
EKONOMIA MATEMATYCZNA 09.03.2014, IV rok, Wykłady, Ekonomia matematyczna
EKONOMIA MENADŻERSKA 04.04.2014, IV rok, Wykłady, Ekonomia menadżerska
EKONOMIA MENADŻERSKA 07.03.2014, IV rok, Wykłady, Ekonomia menadżerska
EKONOMIA MENADŻERSKA 08.03.2014, IV rok, Wykłady, Ekonomia menadżerska
MAKROEKONOMIA ZAAWANSOWANA 25.04.2014, IV rok, Wykłady, Makroekonomia zaawansowana
MAKROEKONOMIA ZAAWANSOWANA 08.03.2014, IV rok, Wykłady, Makroekonomia zaawansowana
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 05.04.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 27.04.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 22.03.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMIA MATEMATYCZNA 09.03.2014, IV rok, Ćwiczenia, Ekonomia matematyczna
EKONOMIA MATEMATYCZNA 23.03.2014, IV rok, Ćwiczenia, Ekonomia matematyczna
EKONOMIA MIĘDZYNARODOWA 16.11.2014-uzupełnienie, V rok, Wykłady, Ekonomia międzynarodowa
EKONOMIA MIĘDZYNARODOWA 30.11.2014-uzupełnienie, V rok, Wykłady, Ekonomia międzynarodowa
EKONOMETRIA 11.05.2012, II rok, Wykłady, Ekonometria
EKONOMIA MIĘDZYNARODOWA 16.11.2014-uzupełnienie, V rok, Wykłady, Ekonomia międzynarodowa
Test z neurologii - 29.05.09, IV rok, IV rok CM UMK, Neurologia, giełdy z maila, giełdy, giełdy neur
zebrane-opisówki-patomorfa-2010-2014, IV rok, IV rok CM UMK, Patomorfologia, rozwiązane
więcej podobnych podstron