LISTA 2 OPTYMALIZACJA
UWAGA funkcje:
1)Maple
* diff(fun,x) -pochodna
* subs(x=3,fun) -podstawianie wartości x do funkcji
*roots(fun) -pierwiastki równania
%%%%%%%%%%%% ćw 1 %%%%%%%%%%%%%%%
fun=inline('x.^2./2-sin(x)');
funprim=inline('x-cos(x)');
funbis=inline('1+sin(x)');
xinit=0.5
epsi=0.0001
maxiter=5
[x,f,ok,count]=newton1D(fun,funprim,funbis,xinit,epsi,maxiter)
x = 0.7391
f = -0.4005
ok =1 %minimum
count =2 %iteracje
%liczba iteracji może zostać przekroczona gdy zmieni się
punkt startowy
_____________________________________________
dla sinusa
fun=inline('sin(x)');
funprim=inline('cos(x)');
funbis=inline('-sin(x)');
[x,f,ok,count]=newton1D(fun,funprim,funbis,0.5,epsi,maxiter)
x =1.5708
f =1
ok =2 % maximum
count =4
[x,f,ok,count]=newton1D(fun,funprim,funbis,-0.5,epsi,maxiter)
x =-1.5708
f =-1
ok =1 %minimum
count =4
___________________________________________________
dla następnej funkcji
fun=inline('x.*atan(x)-0.5*log(1+x.^2)')
funprim=inline('atan(x)')
funbis=inline('1/(1+x.^2)')
[x,f,ok,count]=newton1D(fun,funprim,funbis,xinit,epsi,maxiter)
x =0
f =0
ok =1
count =4
______________
xinit=1.5
[x,f,ok,count]=newton1D(fun,funprim,funbis,xinit,epsi,maxiter)
Warning: przekroczona liczba iteracji w newton1D
> In c:\windows\pulpit\nasz\newton1d.m at line 30
Warning: One or more output arguments not assigned during call to 'newton1D'.
x =
3.8950e+006
ok =
0
count =
6
%%%%%%%%%%%%%% ćw 2 %%%%%%%%%%%%%%
f=inline('-x.^5./5-77.*x.^4./240+71.*x.^3./360-7.*x.^2./120+x./120')
f =
Inline function:
f(x) = -x.^5./5-77.*x.^4./240+71.*x.^3./360-7.*x.^2./120+x./120
» fmin(f,0,1)
ans =
0.9999
znalezione min globalne
zgodnie z obliczoną w treści pochodną są cztery punkty
stacjonarne.
????
%%%%%%%%%%%%%% ćw 3 %%%%%%%%%%%%%%%
a)
fun=inline('x.*(x-1).^2')
funprim=inline('(x-1).^2+2*x.*(x-1)')
funbis=inline('4.*(x-1)+2*x')
wybór xo=0 :
[x,f,ok,count]=newton1D(fun,funprim,funbis,0,epsi,maxiter)
x =0.333
f =0.1481
ok =2 % maximum
count =4
wybór x0=1.5:
[x,f,ok,count]=newton1D(fun,funprim,funbis,1.5,epsi,maxiter)
x =1.0000
f =1.2509e-024
ok =1 % minimum
count =4
b)
fun=inline('x/(x.^2+1)')
funprim=inline('(-x.^2+1)/(x.^2+1).^2')
funbis=inline('(2*x.^5-4*x.^3-6*x)/(x.^2+1).^4')
dla x0= 0.5
[x,f,ok,count]=newton1D(fun,funprim,funbis,0.5,epsi,maxiter)
x =1.0000
f =0.5000
ok=2 % maximum
count =4
dla x0= 1.5
[x,f,ok,count]=newton1D(fun,funprim,funbis,1.5,epsi,maxiter)
x=-1.0000
f =-0.5000
ok =1 % minimum
count =5
%%%%%%%%%%%% ćw4 %%%%%%%%%%%%%%%%
fun=inline('2.*sin(x)+3.*cos(x)')
funprim=inline('2.*cos(x)-3.*sin(x)')
funbis=inline('-2.*sin(x)-3.*cos(x)')
Dla (a=2,b=3)
[x,f,ok,count]=newton1D(fun,funprim,funbis,-1.5,epsi,maxiter)
x =-2.5536
f =-3.6056
ok =1
count =4
wartośćmin=-sqrt(4+9)=-3.6056
warośćmin(x=-2.5536)=feval(fun,x) =3.6056
dla(a=3,b=4)
fun=inline('3.*sin(x)+4.*cos(x)')
funprim=inline('3.*cos(x)-4.*sin(x)')
funbis=inline('-3.*sin(x)-4.*cos(x)')
[x,f,ok,count]=newton1D(fun,funprim,funbis,-1.5,epsi,maxiter)
x =-2.4981
f =-5
ok =1
count =3
wartośćmin=-sqrt(9+16)= -5
warośćmin(x=-2.4981)=feval(fun,x)= -5
zastosowanie funkcji fminu:
nm=fminu(fun,-1.5)
nm =-2.4981
lub funkcji fmins:
nm=fmins(fun,-1.5)
nm =-2.4981
do znalezienia minimum
w MAPLE
fun:=a*cos(phi)+b*sin(phi):
> diff(",phi); % pochodna
-a sin(phi) + b cos(phi)
> rozw:=solve(",phi); % rozwiązanie
rozw := arctan(b/a)
> subs(phi=-sqrt(a^2+b^2),fun); % podstawienie z phi podanej wartosci
2 2 1/2 2 2 1/2
a cos(-(b + a ) ) + b sin(-(b + a ) )
%%%%%%%%%%%%%% ćw5 %%%%%%%%%%%%%%%
fun=inline('x.^(2/3)-1')
funprim=inline('2/3.*x.^(-1/3)')
funbis=inline('-2/9.*x.^(-4/3)')
_ Warning: przekroczona liczba iteracji w newton1D
> In c:\windows\pulpit\nasz\newton1d.m at line 30
Warning: One or more output arguments not assigned during call to 'newton1D'.
x =-1.1529e+018 + 1.1909e+003i
ok = 0
count = 30
________
feval(fun,0)
ans =
-1
feval(funprim,0)
ans =
Inf
_________
pierwsza pochodna w punkcie x-0 w lim praw jest >0, a w lim le nie okreslona
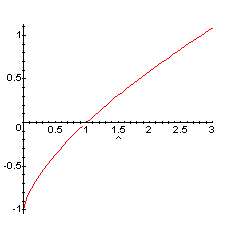
%%%%%%%%%%%% ćw6 %%%%%%%%%%%%%%%%%
fun=inline('abs(x)')
mn=fmins(fun,0)
mn =0
%%%%%%%%%%% ćw7 %%%%%%%%%%%%%%%%%
fun=inline('exp(-x)-cos(x)')
funprim=inline('-exp(-x)+sin(x)')
funbis=inline('exp(-x)+cos(x)')
[x,f,ok,count]=newton1D(fun,funprim,funbis,0.5,epsi,maxiter)
x =0.5885
f =-0.2766
ok=1 % minimum
count =2
[x,f,ok,count]=newton1D(fun,funprim,funbis,2,epsi,maxiter)
x =25.1327
f =-1.0000
ok =1
count =6
wniosek - patrz rysunek
minima w zależności od wybranego punktu początkowego
%%%%%%%%%%%%%%% ćw 8 %%%%%%%%%%%%%%%%
fun=inline('x.^4-14.*x.^3+60.*x.^2-17.*x')
funprim=inline('4.*x.^3-42.*x.^2+120.*x-17')
funbis=inline('12.*x^2-84.*x+120')
[x,f,ok,count]=newton1D(fun,funprim,funbis,1,epsi,maxiter)
x =0.1494
f =-1.2468
ok =1
count =4
____________________________
obliczanie pierwiastków funprim
a=[4,-42,120,-17]
» r=roots(a)
r =
5.1753+ 1.2923i % zespolone
5.1753- 1.2923i % zespolone
0.1494 % !!!
%%%%%%%%%%%%%%%% ćw 9 %%%%%%%%%%%%%%
równanaia:
Pp=(15-2x)*(9-2x)
v=Pp*h
v=(15-2*x)*(9-2*x)*x
fun=inline('4.*x.^3-48.*x.^2+135.*x')
funprim=inline('12.*x.^2-96.*x+135')
funbis=inline('24.*x-96')
[x,f,ok,count]=newton1D(fun,funprim,funbis,1,epsi,maxiter)
x =1.8206
f =110.8191
ok =2
count =3
%%%%%%%%%%%%%% ćw 10 %%%%%%%%%%%%%
równania:
obw=12
obw=2*x+2*y+pi/2*x
zatem
y=-x-pi/4*x+6
P=(pi*x)/4+x*y
zatem podstawiając y
P=-x^2+6*x
fun=inline('-x.^2+6*x')
funprim=inline('-2.*x+6')
funbis=inline('-2')
[x,f,ok,count]=newton1D(fun,funprim,funbis,1,epsi,maxiter)
x =3
f =9
ok =2
count =1
więc:
x=3
y=3-3/4*pi
%%%%%%%%%%%%%%%% ćw 11 %%%%%%%%%%%%%%%
równania:
z trójkąt prost. 7^2+x^2=y^2
y=sqrt(49+x^2)
zatem
dł= (12-x)*6000+9000*(sqrt(49+x^2))
fun=inline('72000-6000.*x+9000.*(49+x.^2).^(1/2)')funprim=inline('-6000+9000./(49+x.^2).^(1/2).*x')
funbis=inline('-9000./(49+x.^2).^(3/2).*x.^2+9000./(49+x.^2).^(1/2)')
[x,f,ok,count]=newton1D(fun,funprim,funbis,1,epsi,maxiter)
x =6.2610
f =1.1896e+005
ok =1
count =4
zatem
x=6.2610
%%%%%%%%%%%%%%% ćw 12 %%%%%%%%%%%%%%%%%%
?
%%%%%%%%%%%%%%%% ćw 13 %%%%%%%%%%%%%%%
UDOWODNIĆ Z DEFINICJI GRADIENDU I HESIANU ORAZ WARUNKÓW NA MAX DWÓCH ZMIENNYCH
%%%%%%%%%%%%%%%% ćw 14 %%%%%%%%%%%%
???
fun= 1/x+x>=2
funprim=-1/x^2+1>=0 => -1/x^2>= -1 => x^2>=1 => x>=1
%%%%%%%%%%%%%%% ćw 15 %%%%%%%%%%
_____ budowa grad _________
function g = grad(x)
g = [22*x(1)-2-20*x(2)^2 -40*(x(1)-x(2)^2)*x(2)];
_______________________________________________
_________ budowa hessian _____________
function H = hessian(x)
H = [ 22 -40*x(2) -40*x(2) 120*x(2)^2-40*x(1)];
_____________________________________________________
fun=inline('(x(1)-1).^2+10.*(x(1)-x(2).^2)^2')
fungrad=inline('grad(x)')
funhess=inline('hessian(x)')
_____dla :______
x=[3;2]
[x, f, ok, count] = newtonND(fun, fungrad, funhess, x, 0.0001, 16)
x =
1.0000
1.0000
f = 5.6264e-017
ok =1 %minimum
count =6
_____dla:_______
x=[3;-2]
[x, f, ok, count] = newtonND(fun, fungrad, funhess, x, 0.0001, 16)
x =
1.0000
-1.0000
f =5.6264e-017
ok =1 % minimum
count =6
____________ dla :_____
x=[0.5;0.2]
[x, f, ok, count] = newtonND(fun, fungrad, funhess, x, 0.0001, 16)
x =
0.0909
0.0000
f = 0.9091
ok =3 % punkt siodłowy
count =5
rysunek maple
plot3d((x1-1)^2+10*(x1-x2^2)^2,x1=0.08..0.1,x2=-0.01..0.01);
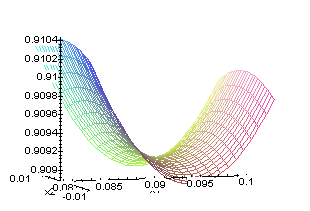
%%%%%%%%%%%%% ćw 16 %%%%%%%%%%%%%%%
Maple:
f=x1^2+4*x1*x2+5*x2^2;
2 2
f = x1 + 4 x1 x2 + 5 x2
> diff(",x1);
>
0 = 2 x1 + 4 x2
> diff(",x2);
0 = 4 x1 + 10 x2
solve({0 = 2*x1+4*x2,0 = 4*x1+10*x2},{x1,x2});
{x2 = 0, x1 = 0}
wykres Maple
plot3d(x1^2+4*x1*x2+5*x2^2,x1=-10..10,x2=-10..10);
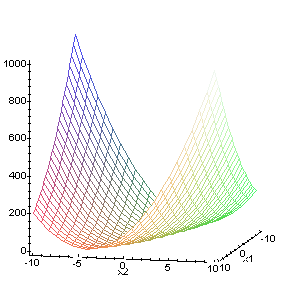
%%%%%%%%% ćw 17 %%%%%%%%%%%%%%
W Maple
f=-x1^2-6*x2^2-23*x3^2-4*x1*x2+6*x1*x3+20*x2*x3;
2 2 2
f = -x1 - 6 x2 - 23 x3 - 4 x1 x2 + 6 x1 x3 + 20 x2 x3
> diff(",x1);
0 = -2 x1 - 4 x2 + 6 x3
> diff(",x2);
0 = -12 x2 - 4 x1 + 20 x3
> diff(",x3);
0 = -46 x3 + 6 x1 + 20 x2
> solve({0 = -2*x1-4*x2+6*x3,0 = -12*x2-4*x1+20*x3,0 = -46*x3+6*x1+20*x2},{x1,x2,x3});
{x3 = 0, x2 = 0, x1 = 0}
%%%%%%%%%%% ćw 18 %%%%%%%%%%%%%%
w Maple
ff=x1^2+x2^2+b*x1*x2+x1+2*x2;
>
2 2
ff = x1 + x2 + b x1 x2 + x1 + 2 x2
> a=diff(",x1);
a = (0 = 2 x1 + b x2 + 1)
> b=diff(",x2);
b = (0 = 2 x2 + b x1 + 2)
> solve({0 = 2*x1+b*x2+1,0 = 2*x2+b*x1+2},{x1,x2});
-1 + b -4 + b
{x1 = -2 -------, x2 = - -------}
2 2
-4 + b -4 + b
__________drugie pochodne _________
diff(2*x1+b*x2+1,x1); % x1,x1
2
> diff(2*x1+b*x2+1,x2); % x1,x2
b
diff(2*x2+b*x1+2,x1); % x2,x1
b
> diff(2*x2+b*x1+2,x2); % x2,x2
2
warunek b<>2 i b<>-2 (dziedzina pochodnej)
delta=4-b^2
jeśli delta > to min
4-b^2>0
b należy do przedziału (-2,2)
jeśli delta < 0 to max
4-b^2<0
%%% rozw z Maple %%%%
diff(2*x2+b*x1+2,x2);
2
> as=solve(4-b^2<0);
as = (RealRange(-infinity,Open(-2)), RealRange(Open(2),infinity))
%%%%%%%%%%%%%%%%%%%%%
b należy do przedziału (-nieskończ,-2)sum(2,=nieskoończ)
%%%%%%%%%%%%% ćw 19 %%%%%%%%%%%%%
w Maple
f=(x1^2-4)^2+x2^2;
2 2 2
f = (x1 - 4) + x2
> diff(",x1);
2
0 = 4 (x1 - 4) x1
> diff(",x2);
0 = 2 x2
> solve({0 = 4*(x1^2-4)*x1,2*x2=0},{x1,x2});
{x2 = 0, x1 = 2}, {x2 = 0, x1 = -2}, {x2 = 0, x1 = 0}
zatem trzy punktystacjonarne
_________________________________________________
kod funkcji :
function h=funhess(x)
h=[ 12.*x(1).^2-16 0
0 2];
_______________
function g=fungrad(x)
g=[4.*(x(1).^2-4).*x(1)
2.*x(2)];
fun=inline('(x(1).^2-4).^2+x(2).^2')
funhess1=inline('funhess(x)')
fungrad1=inline('fungrad(x)')
_______dla :______
x=[2;0]
x =
2
0
[x, f, ok, count] = newtonND(fun, fungrad1, funhess1, x, 0.0001, 16)
x =2 0
f =41
ok =1 %minimum
count =0
_______dla :______
x=[0;0]
x =
0
0
[x, f, ok, count] = newtonND(fun, fungrad1, funhess1, x, 0.0001, 16)
x = 0 0
f =1
ok =3 %punkt stacjonarny !!!!!
count =3
_______dla :______
x=[-2;0]
x =
-2
0
[x, f, ok, count] = newtonND(fun, fungrad1, funhess1, x, 0.0001, 16)
x =-2 0
f =49
ok =1 %minimum
count =0
%%%%%%%%%%% ćw 20 %%%%%%%%%
______funkcje________
function g=fungrad(x)
g=[1.0.*x(1)+cos(x(2))
-x(1)*sin(x(2))];
____________
function h=funhess(x)
h=[ 1.0 -sin(x(2))
-sin(x(2)) -x(1)*cos(x(2))];
__________________________
x=[-2;0]
x =
-2
0
[x, f, ok, count] = newtonND(fun, fungrad1, funhess1, x, 0.0001, 16)
x =-1 0
f =-0.5000
ok =1
count =1
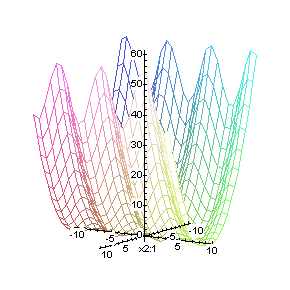
Wyszukiwarka
Podobne podstrony:
L2 Cwiczenia
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
cwiczenia 9 kryzys
Ćwiczenia 1, cz 1
Ćwiczenie 8
9 ćwiczenie 2014
Cwiczenie 1
Ćwiczenie 2 Polska w europejskim systemie bezpieczeństwa
więcej podobnych podstron