Nr ćwiczenia 302	Data 17/04/2012	Imię i nazwisko Mateusz Kaczor	Wydział BMiZ	Semestr II	Grupa ZP3
Prowadząca dr			Przygotowanie	Wykonanie	Ocena

Wyznaczenie stałej siatki dyfrakcyjnej

1. Podstawy teoretyczne

Światło jest falą elektromagnetyczną, tzn. falą polegającą na rozchodzeniu się w przestrzeni zmian natężenia pola elektrycznego i magnetycznego. W zjawiskach optycznych decydującą rolę odgrywa wektor natężenia pola elektrycznego E i to określenie tego wektora w funkcji czasu i współrzędnych przestrzennych wystarcza do opisania fali świetlnej:

Dyfrakcją nazywamy zmianę kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Zjawisko zachodzi dla wszystkich wielkości przeszkód, ale wyraźnie jest obserwowane dla przeszkód o rozmiarach porównywalnych z długością fali.

Interferencją nazywamy nakładanie się dwóch lub większej liczby fal. Prowadzi to do zwiększenia się lub zmniejszenia amplitudy fali wypadkowej. Warunki interferencji można wyrazić zarówno przez różnicę faz
, jak i przez różnicę dróg
:

• maksimum:
  
  
  

• minimum:
  
  
  

Interferencja zachodzi dla dowolnych fal, a ale stały w czasie obraz interferencyjny można zaobserwować tylko wtedy, gdy nakładają się fale spójne (koherentne), tzn. takie, których różnica faz nie zmienia się w czasie.

Dowolny rodzaj fali może ulec zjawisku dyfrakcji lub interferencji. Podstawę wyjaśnienia tych zjawisk stanowi zasada Huyghensa, która mówi, że każdy punkt, do którego dochodzi fala, staje się źródłem nowej fali.

Siatką dyfrakcyjną nazywamy układ równych, równoległych i jednakowo rozmieszczonych szczelin. Urządzenie to służy do przeprowadzania analizy widmowej.

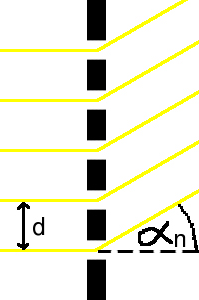
d - stała siatki

α_n - kąt ugięcia fali

Stałą siatki dyfrakcyjnej d nazywamy odległość między środkami sąsiednich szczelin. W celu znalezienia tej wielkości zastosujemy wzór:

d - stała siatki dyfrakcyjnej

λ - długość fali

m = 1, 2, 3...

2. Wyniki pomiarów:

Pomiar położenia prążka zerowego (dla obu siatek):

α_o = 0^o00'

Pomiar położenia prążków po lewej i po prawej stronie:

SIATKA DYFRAKCYJNA „A”		SIATKA DYFRAKCYJNA „B”
LEWA STRONA	PRAWA STRONA	LEWA STRONA	PRAWA STRONA
α1=2^o 50'	α14=2^o 30'	α1=6^o 50'	α4=6^o 45'
α2=5^o 30'	α15=5^o 10'	α2=13^o 40'	α5=13^o 35'
α3=8^o 10'	α16=7^o 50'	α3=20^o 35'	α6=20 ^o 25'
α4=10^o 55'	α17=10^o 30'
α5=13^o 35'	α18=13^o 20'
α6=16 ^o 25'	α19=16 ^o
α7=19^o 20'	α20=18^o 40'
α8=22^o 10'	α21=21^o 30'
α9=25^o 10'	α22=24^o 15'
α10=28^o 15'	α23=27^o 15'
α11=31^o 25'	α24=30^o 10'
α12=34^o 40'	α25=33^o 15'
α13=38^o	α26=36^o 25'

3. Obliczenia

*Obliczenie kątów ugięcia siatki dyfrakcyjnej „A”:

| α0- α1|=|0^o00'-2^o50'|=2^o 50' | α0- α2|=|0^o00'-5^o 30'|=5^o 30' | α0- α3|=8^o 10' | α0- α4|=10^o 55' | α0- α5|=13^o 35' | α0- α6|=16 ^o 25' | α0- α7|=19^o 20' | α0- α8|=22^o 10' | α0- α9|=25^o 10' | α0- α10|=28^o 15' | α0- α11|=31^o 25' | α0- α12|=34^o 40' | α0- α13|=38^o

| α14- α0|=|2^o 30'-0^o00'|=2^o 30' | α15- α0|=|5^o 10'-0^o00'|=5^o 10' | α16- α0|=7^o 50' | α17- α0|=10^o 30' | α18- α0|=13^o 20' | α19- α0|=16 ^o | α20- α0|=18^o 40' | α21- α0|=21^o 30' | α22- α0|=24^o 15' | α23- α0|=27^o 15' | α24- α0|=30^o 10' | α25- α0|=33^o 15' | α26- α0|=36^o 25'

*Obliczenie kątów ugięcia siatki dyfrakcyjnej „B”:

| α0- α1|=|0^o00'-6^o 50'|=6^o 50' | α0- α2|=|0^o00'-13^o 40'|=13^o 40' | α0- α3|=20^o 35'

| α4- α0|=6^o 45' | α5- α0|=13^o 35' | α6- α0|=20 ^o 25'

*Obliczenie stałej siatki dyfrakcyjnej z każdego pomiaru siatki dyfrakcyjnej A:

Długość fali lampy sodowej λ=589,6 nm

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie stałej siatki dyfrakcyjnej dla

Obliczenie wartości średniej stałej siatki dyfrakcyjnej:

4. Dyskusja błędów

Obliczenie odchylenia standardowego:

Pomnożenie odchylenia standardowego przez współczynnik Studenta-Fishera:

5. Wnioski

Obliczone stałe siatki dyfrakcyjne dla poszczególnych prążków nie różnią się znacznie od siebie. Odchylenie standardowe, czyli błąd pomiarów stałej siatki dyfrakcyjnej jest bardzo małe. Stałą siatki dyfrakcyjnej za pomocą przyrządów w laboratorium można określić bardzo precyzyjnie.

2

---