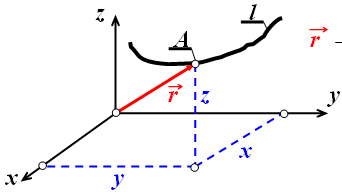
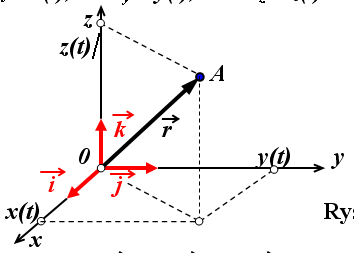
RUCHEM CIAŁA nazywamy zachodzącą w czasie zmianę jego położenia względem innego ciała, które umownie przyjmujemy za nieruchome. RÓWNANIE RUCHU PUNKTU WE WSPÓŁRZĘDNYCH PROSTOKĄTNYCH. r - promień wektor W przypadku gdy punkt porusza się, czyli zmienia z upływem czasu swoje położenie wówczas x = f1(t), y = f2(t), z = f3(t) TOR RUCHU - linia będąca miejscem geometrycznym chwilowych położeń punktu (linia l) Jeśli torem punktu jest linia płaska to może być np. z = con. wtedy: x = f1(t), y = f2(t) PROMIEŃ WEKTOR - jest fukcją wektorową czasu i oznaczamy to r = r(t). Jeśli początek r pokrywa się z początkiem układu 0xyz to rx = x(t), ry = y(t), rz = z(t) r = i x(t) + j y(t) r = i x(t) + j y(t) + k z(t) +kz(t)

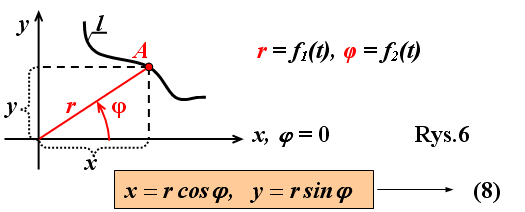
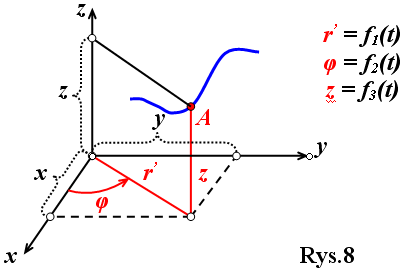
Torem punktu A jest parabola przedstawiona na rys.5. Jak wynika z równań ruchu (6), współrzędne poruszającego się punktu muszą spełniać następujące warunki: -a ≤x ≤ a , 0 ≤ y ≤ b Torem punktu nie jest cała parabola a tylko jej łuk A1,Ao,A2. W chwili początkowej tj. t = 0 punkt znajduje się w wierzchołku paraboli Ao. 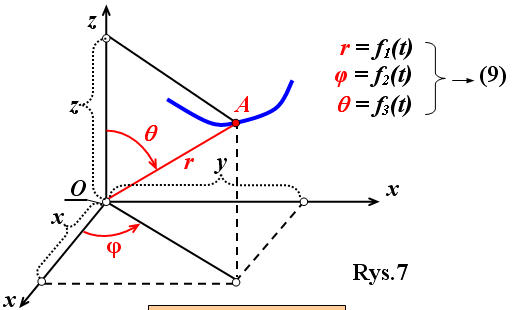Równania ruchu punktu we współrzędnych krzywoliniowych Współrzędne biegunowe na płaszczyźnie Współrzędne biegunowe w przestrzeni x= r sinθ cosφ y= r sinθ sinφ z = rcosθ

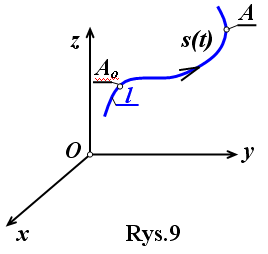
Współrzędne walcowe Równanie ruch punktu na torze Gdy punkt A porusza się po torze, współrzędna s jest pewną funkcją czasu. Równanie ruchu ma wtedy postać: s= ƒ(t) równanie to nosi nazwę równanie ruchu punktu na torze. Jeśli dla t = 0 jest s = 0 i s(t) jest rosnące to s jest drogą punktu A w czasie t.

---