17. Pęd, energia i masa w Szczególnej Teorii Względności

i. Nowe spojrzenie na pęd

Wyobraźmy sobie, że kilku obserwatorów - każdy w innym inercjalnym układzie odniesienia - bada izolowane zderzenie dwóch cząstek. W przypadku nierelatywistycznym każdy z obserwatorów mierzy różne prędkości zderzających się cząstek, ale wszyscy twierdzą, że spełniona jest zasada zachowania pędu. Zgodnie stwierdzają oni, że pęd po zderzeniu cząstek jest taki sam, jak przed zderzeniem.

Jak wygląda to z punktu widzenia teorii względności?

Troszkę inaczej ;)

Rozważmy cząstkę poruszającą się ze stałą prędkością v w dodatnim kierunku osi x

-w ujęciu nierelatywistycznym pęd cząstki ma wartość:

-z kolei w ujęciu relatywistycznym pęd cząstki będzie wyglądał:

gdzie m_r to masa relatywistyczna - wielkość względna (jej wartość zależy od układu odniesienia), może ona zmieniać się bez zmiany zachodzącej w samym obiekcie fizycznym, wyłącznie przez zmianę układu odniesienia

wzór na masę relatywistyczną wygląda następująco:

gdzie m₀ to masa spoczynkowa (in. masa niezmiennicza lub po prostu masa) - wielkość fizyczna w fizyce relatywistycznej, charakteryzująca ciało bądź układ ciał, która nie zależy od układu odniesienia. W dowolnym układzie odniesienia, masa spoczynkowa jest wyznaczona przez energie i pędy wszystkich ciał

Tak więc właściwie pęd relatywistyczny różni się od pędu nierelatywistycznego zaledwie obecnością współczynnika Lorentza γ:

Pęd relatywistyczny dąży do nieskończoności gdy prędkość v dąży do prędkości światła c

Równanie na pęd relatywistyczny
poprawnie definiuje pęd dla wszystkich fizycznie dozwolonych prędkości. W przypadku prędkości znacznie mniejszych od prędkości światła redukuje się do znanej z mechaniki postaci
.

ii. Nowe spojrzenie na energię

a. Energia spoczynkowa

Chemia bardzo długo rozwijała się w założeniu, że w reakcjach chemicznych energia i masa są zachowywane niezależnie od siebie. W 1905 Einstein wykazał w opracowanej przez siebie teorii względności że masę należy rozpatrywać jako jedną z postaci energii, a zasada zachowania energii jest tak naprawdę zasadą zachowania masy i energii.

Zmianę masy można wyraźnie dostrzec podczas reakcji jądrowych w których wyzwalana jest gigantyczna energia.

Masa m i równoważna jej energia E₀ są powiązane ze sobą zależnością:

Energia związana z masą ciała nosi nazwę energii spoczynkowej. Nazwa ta mówi że energię E₀ ma ciało wtedy kiedy spoczywa i jest wyłącznie konsekwencją tego że ciało ma masę.

Wartości energii spoczynkowej wybranych ciał
Ciało	Masa ciała [kg]	Energia spoczynkowa [eV]
elektron	kg	511 keV
proton	kg	938 MeV
atom uranu	kg	225 GeV

b. Energia całkowita
Równanie
wyraża energię spoczynkową związaną z masą ciała m. Energia ta nie zależy od tego czy ciało spoczywa czy porusza się. Kiedy natomiast ciało jest w ruchu ma dodatkową energię w postaci energii kinetycznej E_k. Jeżeli założymy że energia potencjalna jest równa 0 to energia całkowita E będzie równa sumie energii spoczynkowej i kinetycznej:

Energię całkowitą E można również zapisać równaniem:

Zasada zachowania energii całkowitej obowiązuje niezależnie od tego co się dzieje z energią spoczynkową

Zmianę energii spoczynkowej układu, spowodowaną zachodzącą w nim reakcją chemiczną lub jądrową, przyjęło się oznaczać symbolem Q i nazywać energią reakcji. Wartość Q można obliczyć posługując się następującym równaniem:

wiedząc że
dostajemy

czyli:

gdzie

oznacza zmianę masy układu w wyniku reakcji

Jeżeli część energii spoczynkowej ulega przemianie na przykład w energię kinetyczną, przekazywaną produktom w reakcji to całkowita energia spoczynkowa E₀ układu zmniejsza się a energia reakcji Q jest dodatnia. Przeciwnie się dzieje jeśli reakcja wymaga aby energia zamieniła się w energię spoczynkową, wtedy całkowita energia spoczynkowa E₀ układu rośnie a energia reakcji Q jest ujemna.

c. Energia kinetyczna

Wzór znany dobrze z mechaniki na energie kinetyczną ma postać:

Wzór ten ma tylko wtedy rację bytu gdy prędkość ciała jest znacznie zmniejsza od prędkości światła

Przekształcając wzór na energię całkowitą E dostajemy wzór na energię kinetyczną relatywistyczną:

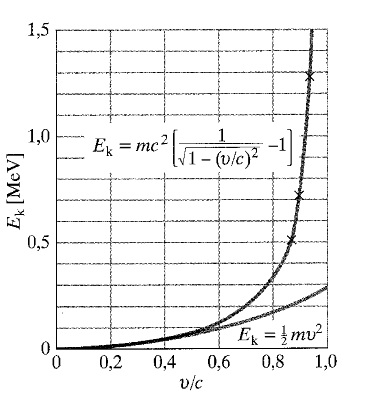
Na wykresie po lewej przedstawiono zależność energii kinetycznej elektronu od stosunku
w przypadku definicji relatywistycznej oraz wobec przybliżenia nierelatywistycznego. Zwróćmy uwagę, że w lewej części wykresu - na obszarze małych prędkości, obydwie krzywe się pokrywają i przybliżenie nierelatywistyczne jest dobre. Jednak kiedy prędkość ciała zbliża się do prędkości światła, krzywe się rozbiegają. Stąd wniosek że wzór nierelatywistyczny jest dobry tylko dla prędkości ciał znacznie mniejszych od prędkości światła.

iii. Pęd a energia kinetyczna
W fizyce nierelatywistycznej pęd cząstki p wyraża się wzorem
, a energia kinetyczna E_k wzorem
. Eliminując prędkość v z obydwu tych wyrażeń można wyznaczyć zależność między pędem a energią kinetyczną:

Podobną zależność można otrzymać w fizyce relatywistycznej analogicznie eliminując prędkość v ze wzoru na pęd i energię kinetyczną:

Korzystając z równania na energię całkowitą możemy powyższe równanie przekształcić tak aby wyrażało zależność między pędem p a całkowitą energią E cząstki

Stąd pęd ciała poruszającego się z prędkością relatywistyczną można wyrazić wzorem:

---