Skalowanie termopary i wyznaczanie temperatury krzepnięcia stopu

Ćwiczenie 20

Cel ćwiczenia: poznanie zjawisk termoelektrycznych oraz przykładów ich zastosowań, a w szczególności zapoznanie się z budową, zasadą działania i pomiarem temperatury za pomocą termopary oraz wyznaczenie temperatury krzepnięcia stopu.

1. Wstęp teoretyczny

1. Skalowanie termopary

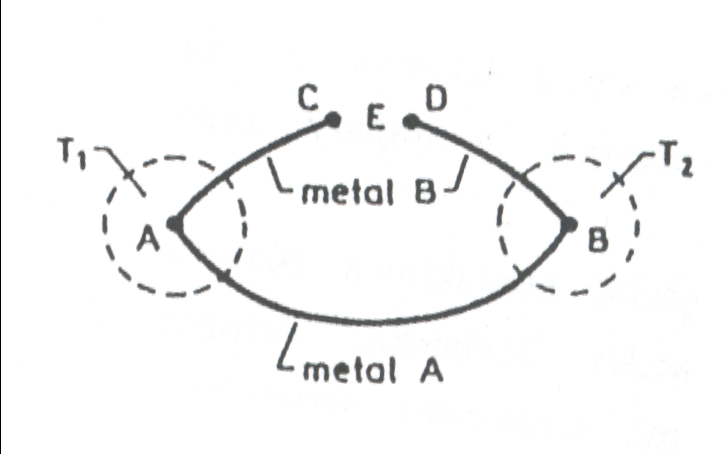
Zjawisko termoelektryczne polegające na powstawaniu różnicy potencjałów na styku dwóch różnych metali jest wykorzystywane do budowy termopar. Termoparą (termoelementem lub termoogniwem) nazywamy obwód zbudowany z dwóch różnych metali lub półprzewodników, którego schemat przedstawiono na rysunku.

Rys.1 Schemat termopary

Jeżeli temperatury złącz różnią się między sobą (T₁≠T₂), to między punktami C i D powstaje siła termoelektryczna E. Siłą ta jest wypadkową różnicy potencjałów Galvaniego oraz Thomsona. Dla niezbyt dużych różnic temperatur między złączami możemy założyć, że siła termoelektryczna jest proporcjonalna do różnicy temperatur T₁ - T₂.

Aby wyznaczyć siłę termoelektryczną E, do obwodu musimy dołączyć miernik. Przewody łączące miernik z termoparą oraz połączenia wewnątrz miernika mogą być wykonane z różnych materiałów. Jeżeli w obwód termopary włączymy inne przewodniki tak, aby temperatury dodatkowych spojeń były jednakowe, to siła termoelektryczna nie ulegnie zmianie (jest to prawo „trzeciego metalu”).

Termopary najczęściej wykonane są z:

• miedzi i konstantanu (40% Ni i 60% Cu) - zakres pomiarowy od 70 K do 800 K

• platyny i platynorodu (90% Pt i 10% Rh) - zakres pomiarowy do 1300 K

• irydu i stopu irydu z rodem - zakres pomiarowy do 2300 K

Warto zwrócić uwagę na to, że siła termoelektryczna termopary zależy od czystości (ilości i rodzaju domieszek) oraz obróbki mechanicznej metali, z których została wykonana. Z tych powodów bardzo istotny jest staranny dobór metali, z których wykonuje się termopary. Bardzo istotne jest także staranne wyskalowanie termopary.

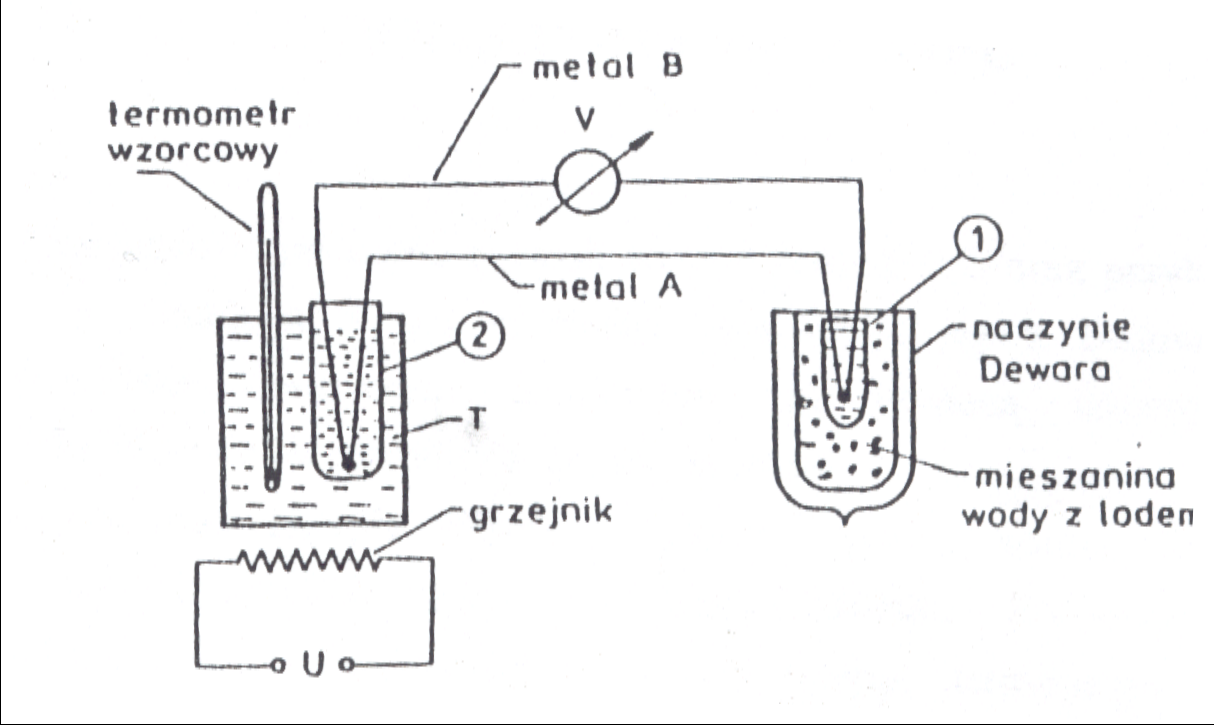
Rys. 2 Schemat układu pomiarowego służącego do skalowania termopary

Skalowanie termopary polega na wyznaczeniu zależności siły termoelektrycznej od różnicy temperatur między spojeniami. Najczęściej jako temperaturę odniesienia przyjmuje się temperaturę 0°C, którą łatwo uzyskać wykorzystując mieszaninę wody z lodem

2. Wyznaczanie temperatury krzepnięcia stopu

Temperaturę krzepnięcia stopu wyznaczamy mierząc zależność temperatury stopu od czasu (podczas stygnięcia). Jeżeli podczas stygnięcia ciała zachodzi przemiana fazowa pierwszego rodzaju, np. krzepnięcie ciała, to z przemianą tą związany jest efekt polegający na wydzielaniu ciepła bez zmiany temperatury ciała.

Ciepłem przemiany fazowej (krzepnięcia, topnienia, parowania, skraplania lub innej) nazywamy ilość ciepła wydzieloną lub pochłoniętą podczas przemiany fazowej bez zmiany temperatury ciała. W temperaturze przemiany fazowej na krzywej stygnięcia pojawia się plateau - pozioma część wykresu. Temperatura, w której jest obserwowane plateau odpowiada temperaturze przemiany fazowej. Długość plateau związana jest z ciepłem przemiany fazowej. Na rysunku przedstawiono schematycznie krzywą stygnięcia dla ciała, w którym zachodzi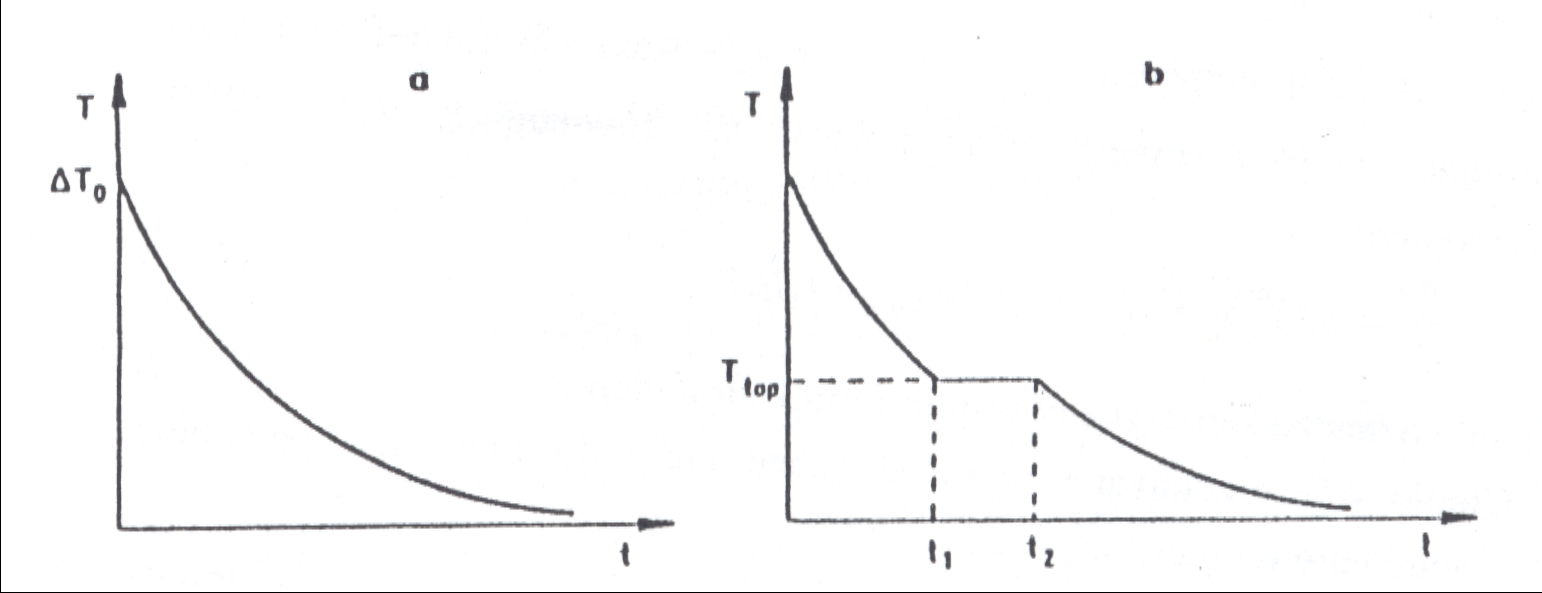
przemiana fazowa pierwszego rodzaju.

Rys. 3 Zależność temperatury stygnącego ciała od czasu: a) wynikająca z równania Newtona; b) dla ciała, w którym występuje przemiana fazowa pierwszego rodzaju

2. Tabele pomiarów

1. Cechowanie termopary

Lp	T1[°C]	T2[°C]	Tśr[°C]	U[mV]	Lp	T1[°C]	T2[°C]	Tśr[°C]	U[mV]
1	26	25	25,5	0,940	18	60	59	59,5	2,399
2	28	27	27,5	1,018	19	62	61	61,5	2,481
3	30	29	29,5	1,104	20	64	63	63,5	2,568
4	32	31	31,5	1,180	21	66	65	65,5	2,658
5	34	33	33,5	1,265	22	68	67	67,5	2,749
6	36	35	35,5	1,348	23	70	69	69,5	2,846
7	38	37	37,5	1,433	24	72	71	71,5	2,931
8	40	39	39,5	1,519	25	74	73	73,5	3,014
9	42	41	41,5	1,602	26	76	75	75,5	3,120
10	44	43	43,5	1,684	27	78	77	77,5	3,201
11	46	45	45,5	1,768	28	80	79	79,5	3,293
12	48	47	47,5	1,868	29	82	81	81,5	3,385
13	50	49	49,5	1,947	30	84	83	83,5	3,490
14	52	51	51,5	2,035	31	86	85	85,5	3,584
15	54	53	53,5	2,125	32	88	87	87,5	3,670
16	56	55	55,5	2,216	33	90	89	89,5	3,765
17	58	57	57,5	2,304

2. Wyznaczanie temperatury krzepnięcia stopu

Lp	U [mV]	t [s]
1	3,88	0
2	3,691	20
3	3,47	40
4	3,259	60
5	3,071	80
6	2,91	100
7	2,777	120
8	2,684	140
9	2,629	160
10	2,609	180
11	2,604	200
12	2,599	220
13	2,594	240
14	2,585	260
15	2,573	280
16	2,563	300
17	2,557	320
18	2,549	340
19	2,54	360
20	2,529	380
21	2,516	400
22	2,496	420
23	2,465	440
24	2,414	460
25	2,341	480
26	2,272	500
27	2,208	520
28	2,152	540
29	2,104	560
30	2,059	580
31	2,018	600
32	1,978	620
33	1,941	640
34	1,91	660
35	1,88	680
36	1,851	700
37	1,826	720
38	1,801	740
39	1,778	760
40	1,757	780
41	1,738	800
42	1,721	820
43	1,705	840
44	1,689	860
45	1,675	880
46	1,659	900
47	1,645	920
48	1,632	940
49	1,619	960

3. Spostrzeżenia i wnioski

• Przy cechowaniu termopary można zauważyć, że napięcie odczytywane na miliwoltomierzu cyfrowym rośnie wprost proporcjonalnie do wzrastającej temperatury.

• Odczytaną z wykresu krzywej stygnięcia stopu wartością napięcia było U = 2,9 mV - jest to tzw. plateau.

• Temperatura, w której jest obserwowane plateau jest równocześnie temperaturą przemiany fazowej.

• Skalowanie termopary służy do wycechowania danej termopary, którą można zastosować do rejestrowania temperatury w dowolnym przetworniku analogowo-cyfrowym. Termopara jest przetwornikiem T/U - temperatura/napięcie.

• Przy użyciu jednej z funkcji arkusza kalkulacyjnego, która daje w wyniku przewidywaną wartość w oparciu o liniową regresję znanych ciągów danych otrzymałem wartość temperatury równą 70,6 °C - jest to temperatura krzepnięcia stopu.

• Badanym stopem był stop Wooda, który zawierał 50% Bi, 25% Pb, 12,5% Cd, 12,5% Sn.

• Doświadczenie dotyczyło badania zjawiska Seebecka. Jako temperaturę odniesienia przyjęto 0 °C

• Błąd pomiaru temperatury był mierzony z dokładnością do 0,5 °C - pomiar był przeprowadzany przy użyciu dwóch termometrów.

• Rezystancja wejściowa miliwoltomierza była bardzo duża i nie miała wpływu na wartości napięcia termoelektrycznego.

1

---