2. ELEMENTARNE WIADOMOŚCI Z RACHUNKU WEKTOROWEGO

Skalar jest to wielkość, którą można określić za pomocą jednej liczby rzeczywistej.

np: masa, temperatura, czas, praca, energia kinetyczna itp.

Wektor jest to wielkość określona liczbą oraz mająca kierunek i zwrot w przestrzeni.

np: siła, prędkość, przyspieszenie itp.

Wektor oznacza się: jedną literą wygrubioną, np. a, lub symbolem AB, gdzie A oznacza początek, zaś B koniec wektora.

Długość odcinka odpowiada, w obranej skali, wartości liczbowej wektora.

Prosta l, na której leży wektor a, nazywa się linią działania wektora.

Wartość bezwzględna wektora nazywa się modułem wektora, który odpowiada długości odcinka .

Moduł wektora oznaczamy następująco:
.

Rodzaje wektorów

• wektory związane z punktem lub wektory uczepione.

• wektory związane z prostą.

• wektory swobodne.

Do określenia wektorów potrzebne są:

• linia działania,

• moduł,

• zwrot

• położenie początku wektora

Wektor związany z punktem lub wektor zaczepiony:

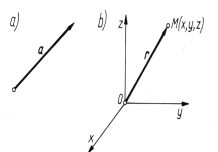
Wektor związany z punktem lub wektor zaczepiony.

• Takich wektorów nie można ani przenosić z miejsca na miejsce, arii nie można przesuwać wzdłuż prostej.

• Jeżeli punkt O uczepienia takiego wektora będzie znajdował się w początku układu współrzędnych, to wektor taki może służyć m.in. do jednoznacznego określenia dowolnego punktu M w przestrzeni — r (promień-wektor)

Wektory związane z prostą:

Do określenia potrzebne są: linia działania, moduł i zwrot.

• Wektora takiego nie można przenosić w dowolne miejsce przestrzeni, lecz można jedynie przesuwać wzdłuż prostej określającej jego położenie (linii działania).

• Wektory tego rodzaju nazywają się: wektorami ślizgającymi się lub wektorami posuwnymi

Wektory swobodne:

• 
  Do określenia nich potrzebne są: moduł, zwrot i kierunek równoległy do linii działania.

• Oprócz tego zasadniczego podziału rozróżniamy następujące rodzaje wektorów swobodnych: równoległe, równe, przeciwne, równoważne, zerowe i jednostkowe (wersory).

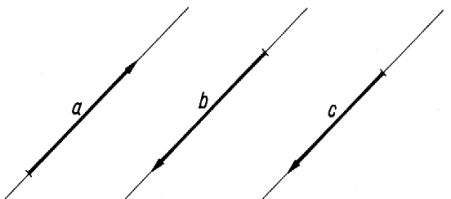
Rodzaje wektorów swobodnych:

• Na rysunku pokazano wektory równoległe, które mają ten sam kierunek w przestrzeni:

• Dwa wektory równoległe, które mają równe moduły oraz te same zwroty, nazywa się wektorami równymi b = c.

• Dwa wektory równoległe mające równe moduły, a przeciwne zwroty nazywa się wektorami przeciwnymi a = - b. Wektory równe b=c mające wspólną siłę działania nazywa się wektorami równoważnymi b=c

Wektor zerowy - wersor

Wektorem zerowym nazywa się wektor, którego moduł jest równy zeru.

Wektor, który ma ten sam kierunek, co wektor dany a, lecz którego moduł równa się jedności, nazywa się wektorem jednostkowym (wersorem) i oznacza się najczęściej takim samym symbolem jak i dany wektor, lecz z indeksem „o”. Na przykład wektorem jednostkowym wektora a jest a₀.

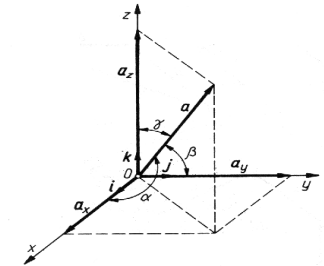
Analityczne przedstawienie wektora wymaga przyjęcia odpowiedniego układu współrzędnych. Najwygodniejszym układem współrzędnych jest układ kartezjański (prostokątny), określony przez trzy wzajemnie prostopadłe osie x, y, z o odpowiednich wersorach i, j, k.

Pokazany na rysunku układ kartezjański jest prawoskrętny, tzn. przy obrocie wersora i w kierunku j wersor k jest skierowany zgodnie z regułą śruby prawoskrętnej. We współrzędnych kartezjańskich wektora jest określony równaniem:

a=a_xi + a_yj + a_zk

gdzie: a_x, a_y, a_z - współrzędne wektora

Wartość wektora a (moduł) jest równa:

a cosinusy kątów, jakie wektor a tworzy z osiami współrzędnych x,y,z wynoszą:

Po wyrażeniu wektora a przez iloczyn jego modułu a i wersora a⁰ równanie a=a_xi + a_yj + a_zk przyjmuje postać:

aa⁰=a_xi + a_yj + a_zk

Następnie po podzieleniu obu stron równania przez a oraz uwzględnieniu zależności
otrzyma się:

a⁰=icosα + jcosβ + kcosγ

A więc wersor dowolnego kierunku ma następujące składowe wzdłuż osi x,y,z:

Dodawanie i odejmowanie wektorów

Dodawanie geometryczne

Dodawanie wektorów podlega następującym prawom:

- przemienności: a+b=b+a

- łączności: a+b+c=a+(b+c)=(a+b)+c

Odejmowanie wektorów

Różnicą dwóch wektorów a i b nazywa się wektor d = a =(-b), ktory otrzymamay przez dodanie do wektora a wektora (-b), przeciwnego do wektora b

Mnożenie wektorów:

Iloczyn skalarny a ∙ b = ab cos(a,b)

Iloczyn skalarny spełnia prawa:

• przemienności: a ∙ b = b ∙ a

• rozdzielności: (a + b) ∙ c = a ∙ c + b ∙ c

• łączności mnożenia iloczynu skalarnego przez liczbę m: m∙ ( a ∙ b) = (m ∙ a) ∙ b = a ∙ (m ∙ b)

Prawo łączności

Jeżeli m i n oznaczają skalary, to prawo łączności wynika z równania:

(m ∙ a) ∙ (n ∙ b) = (m ∙ n) ∙ (a ∙ b)

Na podstawie: a ∙ b = ab(cos a,b), można rozpatrzyć:

a ↓↓ b cos(a,b)=1 a ∙ b = ab

a ↓↑ b cos(a,b)=-1 a ∙ b = -ab

a _|_ b cos(a,b)=0 a ∙ b = 0

a = b cos(a,b)=1 a ∙ b = a²

Z własności iloczynu skalarnego wynikają następujące związki między wektorami jednostkowymi ( wersorami):

i∙i = j∙j = k∙k = 1

i∙j = j∙k = k∙i = 0

a∙b = (a_xi+a_yj+a_zk)(b_xi+b_yj+b_zk) = =a_xb_xii+a_xb_yij+a_xb_zik+a_yb_xji+a_yb_yjj+a_yb_zjk+a_zb_xki+a_zb_ykj+a_zb_zkk = a_xb_x+a_yb_y+a_zb_z

Iloczyn wektorowy

Iloczyn wektorowy dwóch wektorów ( a x b) jest to wektor, którego moduł równa się iloczynowi modułów wektorów składowych przez sinus kąta zawartego między nimi:

c = a x b, c = ab sin (a,b)

Iloczyn wektorowy spełnia :

- prawo rozdzielności ( w odniesieniu do sumy wektorów),

(a+b)×c = a × c + b× c

c × (a + b) = c × a + c × b

lub:

(a + b) × (c + d) = a × c + a × d + b × c + b × d

Moduł iloczynu wektorowego wzrośnie m - krotnie, jeżeli jeden z jego czynników pomnożymy przez skalar m lub wzrośnie (mn) - krotnie, jeżeli jeszcze drugi czynnik pomnożymy przez skalar n.

m (a×b) = (ma) × b = a × (mb)

(ma) × (nb) = (mn) (a×b)

Iloczyn wektorowy nie spełnia prawa przemienności: a × b = - (b × a)

Moduł iloczynu wektorowego równa się liczbowo polu równoległoboku zbudowanego na wektorach składowych.

F_ABCD = ab sinα

c = a × b, c = ab sin(a,b)

Na postawie wzoru: a + b = b + a można napisać:

a || b sin(a,b) = 0 a × b = 0

a = b sin(a,b) = 0 a × b = 0

a _|_ b sin(a,b) = 1 a × b = ab(a⁰ × b⁰), |a × b| = ab

Z własności iloczynu wektorowego wynikają związki między wektorami jednostkowymi (wersorami):

i×i = j×j = k×k = 0

i×j = k j×k = i k×i = j

j×i = -k k×j = -i i×k = -j

Analityczne wyrażenie iloczynu wektorowego dwóch wektorów a i b ma postać:

Wyznacznik:

Rozwinięcie:

a×b = (a_xi+a_yj+a_zk) × (b_xi+b_yj+b_zk) = a_xb_x(i×i) + a_xb_y(i×j) + a_xb_z(i×k) + a_yb_x(j×i) + a_yb_y(j×j) + +a_yb_z(j×k) + a_zb_x(k×i) + a_zb_y(k×j) + a_zb_z(k×k) = (a_yb_z - a_zb_y)i + (a_zb_x - a_xb_z)j + (a_xb_y - a_yb_x)k

Iloczyn mieszany

Iloczyn ten zwany iloczynem mieszanym jest skalarem; z faktu tego wynikają następujące wnioski:

• jeżeli dwa wektory iloczynu mieszanego są równe, to iloczyn mieszany jest równy zeru (dwa wiersze wyznacznika jednakowe)

• w iloczynie mieszanym można cyklicznie przestawiać wektory, co odpowiada dwukrotnemu przestawieniu wierszy w wyznaczniku:

a∙(b×c) = b∙(c×a) = c∙(a×b)

• inne przestawienia wektorów powodują zmianę znaku na przeciwny:

a∙(b×c) = -a∙(c×b) = -b∙(a×c) = -c∙(b×a)

• iloczyn mieszany równa się liczbowo objętości równoległościanu zbudowanego na wektorach składowych.

14

a

b

c = a x b

A

B

C

D

α

α

D

C

B

A

-c = a x b

b

-a

a)

b)

---