1. Rozkład sygnału okresowego w zespolony szereg Fouriera oraz całkowe przekształcenie Fouriera. Widma sygnałów okresowych, prawie okresowych i impulsowych

Zespolony szereg Fouriera	Całkowe przekształcenie Fouriera
(wzór syntezy)	(wzór analizy)
(wzór analizy)	(wzór syntezy)

W rozwiązaniach zadań należy zwracać szczególną uwagę na różnicę w rysowaniu widm {X_k} i X(jΩ).

1.1 Oblicz i narysuj widmo {X_k} sygnału okresowego o okresie T (rozkładając sygnał w zespolony szereg Fouriera) a) prostokątnego o wypełnieniu D i amplitudzie A; b) trójkątnego symetrycznego o amplitudzie A, c) piłokształtnego o wartości międzyszczytowej 2A (rysunki poniżej).

Odp.

a)
,

dla D = 1/2 sygnał można zapisać w postaci:

b)
, sygnał można zapisać w postaci:

c)
, sygnał można zapisać w postaci:

1.2 Oblicz i narysuj widmo X(jΩ) impulsu a) prostokątnego
; b) trójkątnego symetrycznego o amplitudzie A
; c)
.

Odp.

Dla przykładu a)

.

W przykładzie b) aby uniknąć całkowania przez części i żmudnych obliczeń, należy zauważyć, że symetryczny impuls trójkątny o czasie trwania 2T i amplitudzie A jest splotem własnym impulsu prostokątnego o czasie trwania T i amplitudzie
. Następnie należy skorzystać z właściwości przekształcenia Fouriera i zastąpić splatanie w dziedzinie czasu wymnażaniem widm. Ostatecznie więc
. W każdym przypadku warto sprawdzić, czy wartość otrzymanej funkcji w zerze jest równa polu „pod” sygnałem:
.

1.3 Oblicz widmo symetrycznie przyciętej kosinusoidy:
, przyjmując Ω₀ = 4π/T.

Odp.

Metoda 1 (z definicji przekształcenia Fouriera)

Otrzymaliśmy zatem sumę dwóch funkcji samplujących przesuniętych względem zera o +Ω₀ i -Ω₀.

Metoda 2 (z wykorzystaniem właściwości przekształcenia Fouriera)

Sygnał x(t) można potraktować jako iloczyn nieskończenie długiej kosinusoidy
i okna prostokątnego
. Widmo iloczynu dwóch sygnałów jest splotem ich widm, ważonym przez współczynnik 1/2π:

Ponieważ widmem kosinusoidy s(t) jest para delt Diraca:
, natomiast widmem impulsu (okna) prostokątnego funkcja samplująca:
, więc

.

Splot funkcji z przesuniętą deltą Diraca przesuwa funkcję z zachowaniem jej wartości, ponadto splot jest rozdzielny względem dodawania, zatem ostatecznie

.

1.4 Udowodnij, że na wyjściu filtru o rzeczywistej odpowiedzi impulsowej i znanej transmitancji H(s) przy pobudzeniu sygnałem
pojawi się sygnał
. Wykorzystaj symetrię Hermite'a: H(jΩ)= H*(-jΩ).

Odp.

Sygnał wyjściowy y(t) jest splotem odpowiedzi impulsowej h(t) i pobudzenia x(t), gdzie h(t) jest rzecz jasna transformatą odwrotną transmitancji H(s):

Po podstawieniu w miejsce sygnału x(t) mamy:

Korzystamy ze wzorów Eulera, zamieniając funkcję kosinus na parę zespolonych eksponent:

Pod obiema całkami zmienna t pełni rolę parametru, a zatem

Porównując obie całki z definicją przekształcenia Fouriera, dostajemy:

Liczby zespolone
i
są wartościami charakterystyki amplitudowo-fazowej dla pulsacji Ω₀ i -Ω₀. Ponieważ zgodnie z warunkami zadania odpowiedź impulsowa systemu, h(t), była rzeczywista, zatem charakterystyka amplitudowo-fazowa wykazuje właściwość symetrii Hermite'a: charakterystyka amplitudowa jest funkcją parzystą
, charakterystyka fazowa jest funkcją nieparzystą
. Wynika z tego, że

z czego ostatecznie otrzymujemy:

Zastanówmy się jeszcze nad interpretacją powyższego wzoru. Współczynnik przed funkcją kosinus jest nową amplitudą; sygnał został zatem wzmocniony
razy. Wyraz wolny w argumencie kosinusa jest nowym przesunięciem początkowym; sygnał wyjściowy jest więc przesunięty o
radianów w stosunku do sygnału wejściowego.

Wypływa stąd ważny wniosek, że odpowiedzią systemu liniowego na pobudzenie sinusoidalne jest również sinusoida, a z trzech wielkości, które ją opisują, tj. amplitudy, pulsacji i fazy początkowej, zmianie mogą ulec wyłącznie amplituda i faza.

1.5 Narysuj i zapisz wzorem widmo sygnału x(t) = 1 + sin(t) + cos(πt) + exp(j5t) oraz widmo odpowiedzi y(t) tzw. filtru analitycznego o charakterystyce częstotliwościowej
na pobudzenie x(t).

Odp.

Widmo pobudzenia:

Widmo odpowiedzi:

(sygnał wyjściowy y(t) = 1 + exp(j(t-π/2)) + exp(jπt) + 2exp(j5t))

Filtr analityczny jest przykładem filtru specjalnego, którego zasadniczym zadaniem jest zamiana sinusoidy rzeczywistej (lub sumy sinusoid) w zespoloną (lub w sumę sinusoid zespolonych) z zachowaniem składowej stałej. Sygnał wyjściowy jest nazywany równoważnikiem analitycznym sygnału rzeczywistego x(t), jego moduł
- amplitudą chwilową, natomiast pochodna fazy po czasie
- pulsacją chwilową. Wymienione wielkości mają fundamentalne znaczenie w teorii modulacji. Sygnał y(t) można bowiem przedstawić w postaci:
, czyli jako iloczyn zawsze nieujemnego sygnału
i tzw. fazora zespolonego o - w ogólnym przypadku - zmieniającej się pulsacji chwilowej. Każdy sygnał można traktować jako wynik jednoczesnej modulacji amplitudy i częstotliwości lub fazy. Sinusoida zespolona Aexp(jΩ₀t) jest szczególnym przypadkiem sygnału o stałej amplitudzie chwilowej a(t) = A i stałej pulsacji chwilowej Ω(t) = Ω₀.

2. Próbkowanie

	Min	Max
Częstotliwość sygnału przed próbkowaniem [Hz]	- ∞	+∞
Częstotliwość unormowana [1/Sa]
Częstotliwość po rekonstrukcji [Hz]

2.1 Podaj twierdzenie o próbkowaniu. Jakie zjawisko wystąpi w przypadku niespełnienia jego założeń? Co to jest częstotliwość Nyquista, a co oznacza szybkość Nyquista?

2.2 Falę prostokątną o amplitudzie A, częstotliwości podstawowej F₀ i wypełnieniu D = 50% (patrz: zad. 1.1a)) spróbkowano z szybkością F_S = 8F₀. Wyznacz sygnał po rekonstrukcji. Wskazówka: Narysuj widmo sygnału przed próbkowaniem i po spróbkowaniu, a następnie po rekonstrukcji.

Odp.

2.3 Symetryczny sygnał trójkątny o amplitudzie A i częstotliwości podstawowej F₀ (patrz: zad. 1.1b)) spróbkowano z szybkością F_S = 4F₀. Wyznacz sygnał po rekonstrukcji.

Odp.

Ponieważ

a składowe o częstotliwościach większych niż 2F₀ zostaną zaliasowane, więc sygnał po rekonstrukcji będzie równy:

Tak prosty wynik nie powinien dziwić. Próbkując naszą falę trójkątną dostajemy bowiem następujący ciąg próbek: x[n] = {…, A, 0, -A, 0, A, 0, -A, 0, A, …}. Ciąg ten może być zapisany za pomocą funkcji kosinus:
, co po rekonstrukcji daje sygnał
.

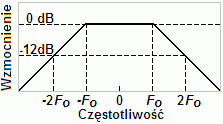
2.4 Sygnał x(t) = 5cos(6000πt) + 4cos(12000πt) + 8cos(24000πt) spróbkowano z szybkością F_S = 8000 Sa/s (próbek na sekundę). Podaj postać sygnału x[n] po spróbkowaniu. Wyznacz amplitudy i częstotliwości składowych tego sygnału po rekonstrukcji. Jaka jest częstotliwość Nyquista? Co się zmieni, gdy sygnał przed próbkowaniem poddamy filtracji antyaliasingowej w filtrze dolnoprzepustowym o charakterystyce amplitudowej jak na rysunku i zerowej charakterystyce fazowej (F₀ = 3 kHz) ?

Zwróć uwagę na dobór częstotliwości granicznej filtru. Jaki ma to związek z szybkością próbkowania i z tym, że filtr aby być realizowalny fizycznie, nie może być idealny?

Odp.

Sygnał po spróbkowaniu:

W powyższym sygnale tylko pierwsza składowa ma częstotliwość unormowaną nie większą od
. Pozostałe składowe wymagają przekształcenia, w którym skorzystamy z tego, że kosinus jest funkcją okresową z okresem 2π.

Sygnał po rekonstrukcji:

W przypadku użycia filtru antyaliasingowego zmienią się amplitudy dwóch składowych. Ze względu na spadek wzmocnienia powyżej częstotliwości F₀ = 3 kHz, wynoszący -12 dB/okt, amplituda składowej o częstotliwości 6 kHz zmniejszy się czterokrotnie, natomiast amplituda składowej o częstotliwości 12 kHz 16 razy. Ostatecznie sygnał po rekonstrukcji będzie miał następującą postać:

W rozwiązaniu należy sprawdzić, czy częstotliwości składowych po rekonstrukcji są nie większe od częstotliwości Nyquista (F_S/2).

Idealny filtr antyaliasingowy powinien mieć prostokątną charakterystykę amplitudową (lub nawet amplitudowo-fazową) o częstotliwości granicznej równej częstotliwości Nyquista. Ponieważ odpowiedź impulsowa takiego filtru jest obustronnie nieskończona, zatem filtru nie można zrealizować fizycznie. W rzeczywistych realizacjach konieczne jest więc użycie filtru, w którym zbocze charakterystyki w paśmie przejściowym ma skończone nachylenie, a częstotliwość graniczna filtru (przeważnie definiowana jako tzw. częstotliwość 3-decybelowa ma mniejszą wartość od F_S/2.

3. Splot (liniowy)

3.1 Oblicz splot sygnałów x[n] i h_k[n], metodą graficzną i metodą algebraiczną, korzystając z właściwości delty Kroneckera. Zwróć uwagę na różnice w sygnałach. Jakie ogólne prawo obrazują?

a) h₁[n] = δ[n] + 2δ[n-1] + 3δ[n-2], x[n] = {1, 2}

b) h₂[n] = δ[n+1] + 2δ[n] + 3δ[n-1], x[n] = {1, 2}

c) h₃[n] = δ[n-1] + 2δ[n-2] + 3δ[n-3], x[n] = {1, 2}

Odp.

Dla przykładu a)

Czyli y₁[n] = {1, 4, 7, 6}. Skorzystaliśmy tu z rozdzielności splotu względem dodawania. Właściwość tę można wykorzystać w przypadku dowolnych sygnałów.

3.2 Znajdź odpowiedzi systemów cyfrowych o danych odpowiedziach impulsowych h[n] na podane sygnały pobudzające x[n], stosując jedną z dwóch metod graficznych. Czy systemy te są typu FIR (SOI) czy IIR (NOI)? Czy są przyczynowe? Które są stabilne?

1. h[n] = u[n], x[n] = u[n] - u[n-N], N > 0;

2. h[n] = u[n] - u[n-N], x[n] = u[n] - u[n-M], 0 < N < M;

3. h[n] = aⁿu[n], x[n] = u[n], 0 < a < 1;

4. h[n] = nu[n], x[n] = u[n] - u[n-N], N > 0;

5. h[n] = aⁿu[n], x[n] = u[n] - u[n-N], N > 0, 0 < a < 1;

6. h[n] = n(u[n] - u[n-N]), x[n] = n(u[n] - u[n-M]), 0 < N < M;

7. h[n] = ၤ[n] - ၤ[n-N], x[n] = u[n] - u[n-M], 0 < N < M;

8. h[n] = ၤ[n] - ၤ[n-N], x[n] = u[n] - u[n-M], 0 < M < N;

9. h[n] = ၤ[n] - ၤ[n-N], x[n] = nu[n], N > 0;

10. h[n] = ၤ[n] + ၤ[n-N], x[n] = nu[n], N > 0;

11. h[n] = ၤ[n+N] - ၤ[n], x[n] = n(u[n] - u[n-M]), 0 < N < M;

12. h[n] = ၤ[n+N] + ၤ[n], x[n] = n(u[n] - u[n-M]), 0 < N < M;

13. h[n] = ၤ[n+N] - ၤ[n], x[n] = n(u[n] - u[n-M]), 0 < M < N;

14. h[n] = ၤ[n+N] + ၤ[n], x[n] = n(u[n] - u[n-M]), 0 < M < N.

Zastanów się, jak zapisać sygnały h[n] i x[n], stosując symbol sumowania.

Odp.

a)
. Oba zapisy (z nawiasem klamrowym i za pomocą skoków jednostkowych) są oczywiście równoważne. W rozwiązaniach wystarczy podać jeden z nich.

System jest typu IIR i jest niestabilny, ponieważ
.

b)

, system typu FIR, stabilny, gdyż suma
jest skończona

c)
, system typu IIR, stabilny dla

i)
, system typu FIR, stabilny

j)
, system typu FIR, stabilny

Systemy z przykładów od a) do j) są przyczynowe, cztery ostatnie - nieprzyczynowe.

3.3 Oblicz odpowiedzi filtrów grzebieniowych o odpowiedziach impulsowych a) h₁[n] = {1, 1}; b) h₂[n] = {1, -1} na sygnał
.

Odp.

a)

Wniosek:
jest nową amplitudą przefiltrowanej sinusoidy, natomiast
jej fazą początkową.

3.4 W kaskadę połączono dwa systemy, jeden o odpowiedzi impulsowej
, drugi o odpowiedzi impulsowej
. Wyznacz wypadkową odpowiedź impulsową h[n].

Odp.

Odpowiedź impulsowa kaskady systemów jest splotem ich odpowiedzi impulsowych:

A stąd

Splot z pierwszym składnikiem h₂[n] wynosi:

Splot z drugim składnikiem:

Odpowiedź impulsowa jest sumą powyższych splotów:

3.5 Wyznacz i naszkicuj odpowiedź systemu o odpowiedzi impulsowej
na pobudzenie ciągiem „rzadkich” delt Kroneckera, opisanym wzorem
, gdzie M > N oznacza odstęp między kolejnymi deltami.

3.6 Zamodeluj w dziedzinie czasu dyskretnego odbicia dźwięku od dwóch równoległych nieskończenie długich i nieskończenie wysokich ścian „pomieszczenia”. Opisz zjawisko wielokrotnego echa za pomocą odpowiedzi impulsowej. Jaki charakter powinna mieć (jaką funkcją należy ją wyrazić), aby odpowiadała zjawisku fizycznemu? Jak obliczyć odpowiedź „pomieszczenia” na dowolny sygnał pobudzający?

3.7 Udowodnij, że wynikiem splotu sygnału z opóźnioną deltą Kroneckera jest opóźnienie sygnału:

Odp.

Dowód przeprowadzimy wprost z definicji:

Ponieważ
, to po rozpisaniu powyższej sumy dostajemy:

,

co należało wykazać.

4. Przekształcenie Z

(proste)

(odwrotne)

4.1 Oblicz transmitancje systemów z zadania 3.2. Napisz równania różnicowe opisujące te systemy.

Odp.

1. 
   , obszar zbieżności (ROC):
   ,
   

2. 
   , obszar zbieżności (ROC):
   ,

3. 
   , obszar zbieżności (ROC):
   ,
   

4. Korzystamy z następującej właściwości: Jeżeli
   , to
   . Wówczas szukana transmitancja wynosi:
   , obszar zbieżności (ROC):
   ,
   

7. 
   , obszar zbieżności (ROC):
   ,
   

12. 
    , obszar zbieżności (ROC):
    ,
    

4.2 Stosując przekształcenie Z, wyznacz odpowiedź systemu o odpowiedzi impulsowej h[n]=(1/3)ⁿu[n] na pobudzenie sygnałem x[n] = (1/2)ⁿu[n]. Czy system jest przyczynowy i czy jest stabilny? Podaj jego równanie różnicowe.

Odp.

Transmitacja systemu:
, transformata pobudzenia:
. Transformata odpowiedzi:

,

gdzie
,

Odpowiedź impulsowa systemu przyjmuje wartości zerowe dla ujemnych chwil n, zatem system jest przyczynowy. W równaniu różnicowym,
, nie występują składniki typu x[n+1], x[n+2] itd. Transmitancja systemu jest funkcją wymierną, w której stopień licznika jest nie większy niż stopień mianownika.

Aby system był stabilny, jego odpowiedź impulsowa musi być bezwzględnie sumowalna lub sumowalna z kwadratem (drugi warunek oznacza, że jej energia jest skończona). Ponieważ

więc system jest stabilny. Aby wykazać, że system jest stabilny na podstawie transmitancji H(z) wystarczy sprawdzić położenie jej biegunów. Jeżeli wszystkie bieguny transmitancji leżą wewnątrz okręgu jednostkowego, czyli ich moduły są nie większe od jedności, system jest stabilny. W naszym przypadku mamy pojedynczy biegun
, więc system jest stabilny.

4.3 Oblicz odpowiedź y[n] systemu DLS y[n] = x[n] + ay[n-1] na pobudzenie sygnałem x[n]=10u[n]. Przyjmij a=1/2. Sprawdź poprawność rozwiązania za pomocą splotu. Oblicz transmitancję H(z) i odpowiedź impulsową h[n] systemu. Czy ten system jest przyczynowy? Czy jest stabilny? (zadanie z egzaminu z PCPS z 2003r., E. Hermanowicz)

Odp.

Z równania różnicowego wyprowadzamy równanie transformat (równanie operatorowe):

,

z którego otrzymujemy transmitancję:

, obszar zbieżności

Wyprowadzamy wzór na transformatę pobudzenia:

, obszar zbieżności

Transformata odpowiedzi jest iloczynem transformaty pobudzenia i transmitancji, zatem:

, obszar zbieżności

Stąd sygnał wyjściowy jest równy:

Jedyny biegun transmitancji H(z),
, leży wewnątrz okręgu jednostkowego, więc system jest stabilny. Ponadto z równania różnicowego, transmitancji lub odpowiedzi impulsowej:
wynika, że jest przyczynowy.

4.4 Wyznacz odpowiedź y[n] systemu o transmitancji H(z) na pobudzenie x[n]. Narysuj schemat systemu. Czy system jest stabilny? Czy jest przyczynowy?

a)
,

b)
,

c)
,

Odp.

a)
, stabilny (biegun transmitancji leży wewnątrz okręgu jednostkowego)

b)
, stabilny (jw.)

c)
, niestabilny (co najmniej jeden z biegunów nie leży wewnątrz okręgu jednostkowego, w tym przypadku żaden z biegunów nie spełnia tego warunku)

Wszystkie systemy są przyczynowe, ponieważ stopnie liczników transmitancji są nie większe od stopni mianowników.

4.5 Dane są sygnały:

a)
,

b)
,

Jaką transmitancję ma system, który pobudzony sygnałem x[n] daje na wyjściu odpowiedź y[n]? Podaj równanie różnicowe opisujące ten system i jego odpowiedź impulsową. Następnie sprawdź metodą splotu, że
. Który z filtrów jest typu FIR, a który IIR? Kiedy są stabilne?

Odp.

a)
,
,

b)
,
,

Metodą splotu rozwiążemy drugi przykład z tego zadania jako mniej trywialny. Skorzystamy tu ze wzoru definicyjnego:

Wymnożenie przez skok jednostkowy otrzymaliśmy z warunku, że suma typu
ma sens tylko wtedy, gdy górna granica sumowania jest nie mniejsza od dolnej. W tym przypadku n musi być nieujemne. Pierwsza próbka sygnału
ma wartość zero, z czego wynika równość sygnałów
i
.

D. Tkaczuk. Zadania z Przetwarzania Sygnałów, rok 2011/2012 (wersja z dn. 7.11.2011)

3

---