Udowodniono, że światło można traktować zarówno jako zbiór cząstek (fotonów) wylatujących ze źródła światła i poruszających się po liniach prostych (korpuskularna teoria światła wyjaśniająca np. bardzo dobrze zjawisko fotoelektryczne czy efekt Comptona), jak też jako falę z wszystkimi charakterystycznymi dla niej własnościami (np. dyfrakcja, interferencja, polaryzacja).
W tym drugim ujęciu światło jest falą elektromagnetyczną, poprzeczną, rozchodzącą się przestrzeni z bardzo dużą prędkością. Do najbardziej spektakularnych zjawisk falowych należą zjawiska związane z interferencją fal świetlnych.
Aby nastąpiła interferencja muszą się spotkać co najmniej dwa ciągi falowe, które są ze sobą spójne.
Do niedawna (zanim nie wymyślono laserów), uzyskanie dwóch spójnych wiązek światła nie było proste. Aby to wyjaśnić należy przypomnieć jaki jest mechanizm powstawania światła.
Otóż elektrony w atomach i cząsteczkach posiadają pewną energię (potencjalną i kinetyczną) związaną z oddziaływaniem z jądrami atomów. Energia ta nie jest dowolna, lecz może przybierać tylko pewne określone wartości (mówimy, że energie elektronów są skwantowane). Elektron może zmienić swą energię tylko wtedy, gdy oddaje do otoczenia (lub pobiera z otoczenia) ściśle określoną porcję energii. Mówimy, że gdy elektron spada z wyższej orbity na niższą (bliższą jądra) to oddaje energię, a gdy przechodzi na orbitę wyższą, musi pobrać energię. Porcja oddawanej lub pobieranej energii musi być dokładnie równa różnicy energii dozwolonych dla tego elektronu orbit.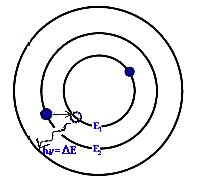

Innymi słowy, tak jak to widać na rysunku obok, elektron przeskakuje z jednego poziomu energetycznego dozwolonego (na którym ma energię E₂)  na inny, niższy (o energii E₁),  oddając porcję energii

odpowiada dokładnie różnicy
E = E₂ - E₁ między dozwolonymi poziomami energetycznymi elektronu.
W ten sposób powstaje światło. Lecz światło z klasycznych źródeł światła nigdy nie jest spójne. Po pierwsze dla tego, że większość źródeł nie daje światła monochromatycznego (o jednej długości fali), lecz określone widmo (bardzo często ciągłe, jak np. żarówka). Po drugie, nawet światło ze źródła monochromatycznego, jak np. używana w tym ćwiczeniu lampa sodowa nie daje światła spójnego. Otóż wiązka światła składa się z fal pochodzących z bardzo wielu promieniujących atomów ciała świecącego. Są one spolaryzowane w zupełnie przypadkowy sposób, a pnadto nakładają się wszystkie na siebie w zupełnie przypadkowych fazach. Aby więc można było zaobserwować interferencję, należy z takiej wiązki wydzielić te fale, które są spójne. Jedną z metod jest rozdzielenie jednej fali na dwie wiązki, a następnie doprowadzenie do ich nałożenia się w odpowiednich fazach. Efekt ten uzyskuje się na przykład w przypadku interferencji światła w cienkich warstwach. "Cienkich" oznacz tu" taką grubość, przy której nie jest przekroczony tzw. zakres spójności fal interferujących, to znaczy, mówiąc w skrócie, aby fala po przejściu owej "cienkiej warstwy" zdążyła jeszcze spotkać się z tą samą wiązką,od której została oddzielona. Zasadę interferencji w cienkiej warstwie omówię w oparciu o rysunek:

Promień monochromatycznego światła padający na płytkę w punkcie A ulega częściowo odbiciu (i biegnie dalej jako promień 1), a częściowo załamaniu. Promień załamany ulega kolejnym odbiciom i załamaniom w punktach B,C i E W rezultacie możemy uzyskać po dwa promienie po każdej stronie płytki. Jeżeli warstwa jest dostatecznie cienka (dla światła widzialnego powinna być rzędu ułamka milimetra), promienie 1 i 2 oraz 3 i 4 mogą ze sobą interferować.
Korzystając z prawa załamania i z prawa odbicia
można wyprowadzić wzór określający warunki, przy których w świetle odbitym powstają ciemne prążki (interferencyjne osłabienie):

lub wzór opisujący powstawanie jasnych prążków:

Jak widać, wynik interferencji zależy zarówno od kąta padania jak i od grubości warstwy.
Powstające prążki interferencyjne nazywamy prążkami jednakowej grubości, gdyż odpowiadają ściśle określonej grubości h warstwy ośrodka. Jeszcze lepiej wyjaśnić tę nazwę omawiając powstawanie pierścieni Newtona. Rolę cienkiej warstwy pełni warstwa powietrza między soczewką a płytką szklaną :

Interferować mogą tylko promienie 3 i 4, gdyż grubość soczewki jest zbyt duża, aby pozostałe promienie były spójne.
Wybierzmy np. prążki ciemne (otrzymamy nieco krótszy wzór) i zastosujmy podaną wyżej zależność przyjmując jako wartość współczynnika załamania n=1 (cienką warstwą jest tu powietrze) oraz sinus równy 0 (promienie padają na soczewkę pionowo z góry, czyli kąt padania jest równy zero). Otrzymamy więc wzór:

h = ¹/₂ k 

Z drugiej strony, z warunków geometrycznych przedstawionych na rysunku:

otrzymujemy:

(R-h)² + r² = R²

a stąd:

r² = 2hR - h²

a ponieważ warstwa jest bardzo cienka, a promień soczewki bardzo duży (u nas promień wynosi ok. 4,3m a grubość warstwy ułamek milimetra) możemy pominąć h² jako bardzo małe.
Tak więc mamy dwa wzory:

r² = 2hR  

   h = ¹/₂ k 

z których otrzymujemy:

r² = k R 

i ostatecznie:

CEL ĆWICZENIA.

Celem ćwiczenia jest wyznaczenie długości fali światła emitowanego przez monochromatyczne żródło światła. Źródłem tym może być np. lampa sodowa, lub dioda elektroluminescencyjna.

WYKONANIE ĆWICZENIA.

1. Włączyć lampę sodową i odczekać około 5min.

2. Ustawić w mikroskopie ostry obraz górnej powierzchni płytki płaskorównoległej (przy pomocy bocznego pokrętła).

3. Aby obraz pierścieni był jasny i kontrastowy, wyregulować oświetlenie za pomocą przesłony, a za pomocą okularu dobrać ostrość widzenia do własnego wzroku.

4. Ustawić soczewkę w taki sposób, aby środek układu pierścieni widocznych w okularze mikroskopu znalazł się na skrzyżowaniu nici i przy ruchu stolika (poziomym i pionowym) przesuwał się wzdłuż nici. Obie śruby mikrometryczne powinny być ustawione w połowie swojej długości (prawa na ok. 25 mm, przednia na ok. 12 mm).

5. Zmierzyć promienie kilkunastu ciemnych pierścieni, przesuwając stolik przy pomocy śruby mikrometrycznej w dół i w górę (pomiar nr 1), a także w prawo i w lewo (pomiar nr 2) w stosunku do środka układu pierścieni. Wewnętrzne pierścienie są dość szerokie, dlatego proponujemy wykonać pomiary dla pierścieni wyższych rzędów, np. poczynając od piątego.

6. Obrócić soczewkę o około 45^o i powtórzyć czynności z punktów 4 i 5 (pomiary nr 3 i 4); powód: wyeliminowanie ewentualnej niesferyczności soczewki.

7. Obliczyć - średnią arytmetyczną z uzyskanych pomiarów dla poszczególnych pierścieni.

Tabela I.
Uwaga: S₂ i S₂ to odczyty ze śruby mikrometrycznej przy położeniach nici pajęczej takich jak na poniższym rysunku ( przedstawione na przykładzie pierścienia piątego (k = 5) i dla prawej śruby mikrometrycznej).


OPRACOWANIE WYNIKÓW POMIARÓW.

METODA I Sporządzić wykres:

(na osi y) od k (oś x).
Stosując metodę regresji liniowej (metodę najmniejszych kwadratów), znaleźć parametr
występujący w równaniu prostej
najlepiej aproksymującej rezultaty pomiarów:

Miarą błędu jest odchylenie standardowe:

Długość fali można wtedy wyznaczyć z równania:

a niepewność pomiarową
z obliczonego wcześniej
.

METODA II

Ponieważ odczyt wartości promienia prążka jest obarczony dość dużym błędem ze względu na niepunktowe przyleganie soczewki do płytki płaskorównoległościennej, lepiej jest zmierzyć promienie dwóch różnych pierścieni, o numerach k₁ i k₂. Pisząc dla tych prążków równanie na kwadrat promienia prążka k₁ i odejmując od niego równanie na kwadrat promienia prążka k₂ (mogą to być dwa jasne lub dwa ciemne prążki) otrzymamy po odjęciu stronami i przekształceniu wzór:

Wówczas należy wypełnić tabelę II.

Tabela II.

Potrzebne do obliczeń dane proszę pobrać z tabeli I (pamiętając o zamianie "r_k" na metry).
obliczyć jako odchylenie standardowe wartości średniej .

UWAGA

Można tu także ściągnąć pełną postać instrukcji stanowiskowej zapisaną w formacie WORD-a





Powrót do
Strony tytułowej

---