AKADEMIA GÓRNICZO - HUTNICZA W KRAKOWIE			Grupa B Rafał Szemraj
EAIiE	2001/2002		Rok II Semestr IV	Elektrotechnika		Rok B Grupa 8
Temat: Reprezentacja stacjonarnych układów liniowych w dziedzinie zmiennej zespolonej s.
Data wykonania: 2002-04-12		Data zaliczenia:			Ocena:

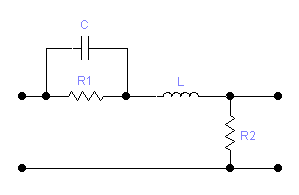
Dane: R1 = 2Ω; R2 = 1Ω; L = 0,2H; C = 0,0001F

Model matematyczny dla powyższego układu:

1. 2.

⇒

z 2-go układu mamy:

a dalej:

Po podstawieniu danych mamy:

Schemat blokowy układu:

Transmitancję zastępczą układu można przedstawić jako równoległe połączenie dwóch członów:

Oscylacyjnego i szeregowego połączenia członu oscylacyjnego (takiego samego jak poprzedni) z członem idealnym różniczkującym:

Wzmocnienie członu różniczkującego idealnego wynosi
a drugiego członu oscylacyjnego

Dla członu oscylacyjnego mamy T = 3,65 ms, tłumienie ξ = 9,14 (tłumienie duże, w odpowiedzi układu brak oscylacji mimo takowego charakteru układu). Ponieważ transmitancja G₂(s) jest członem proporcjonalnym o k = 1 postacie odpowiedzi i(t) i y(t) będą identyczne.

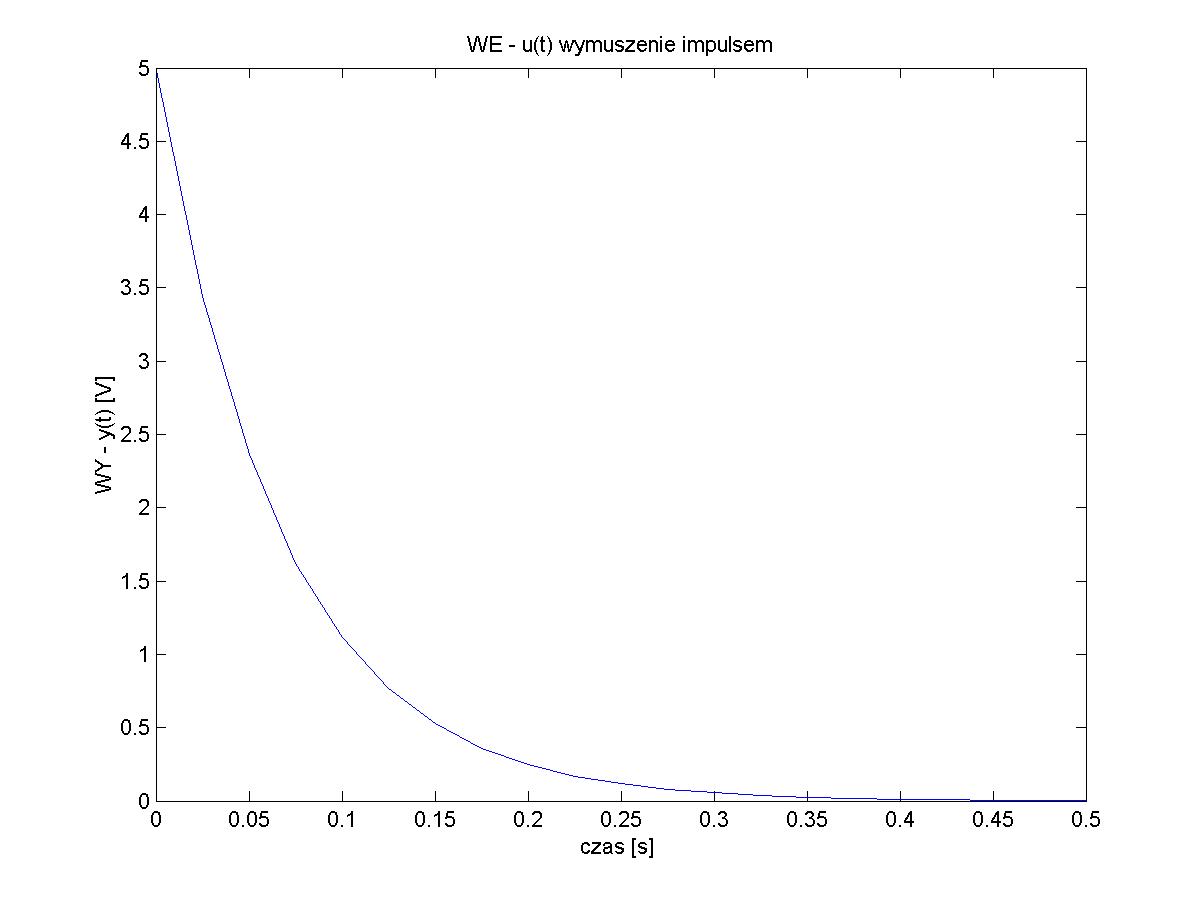
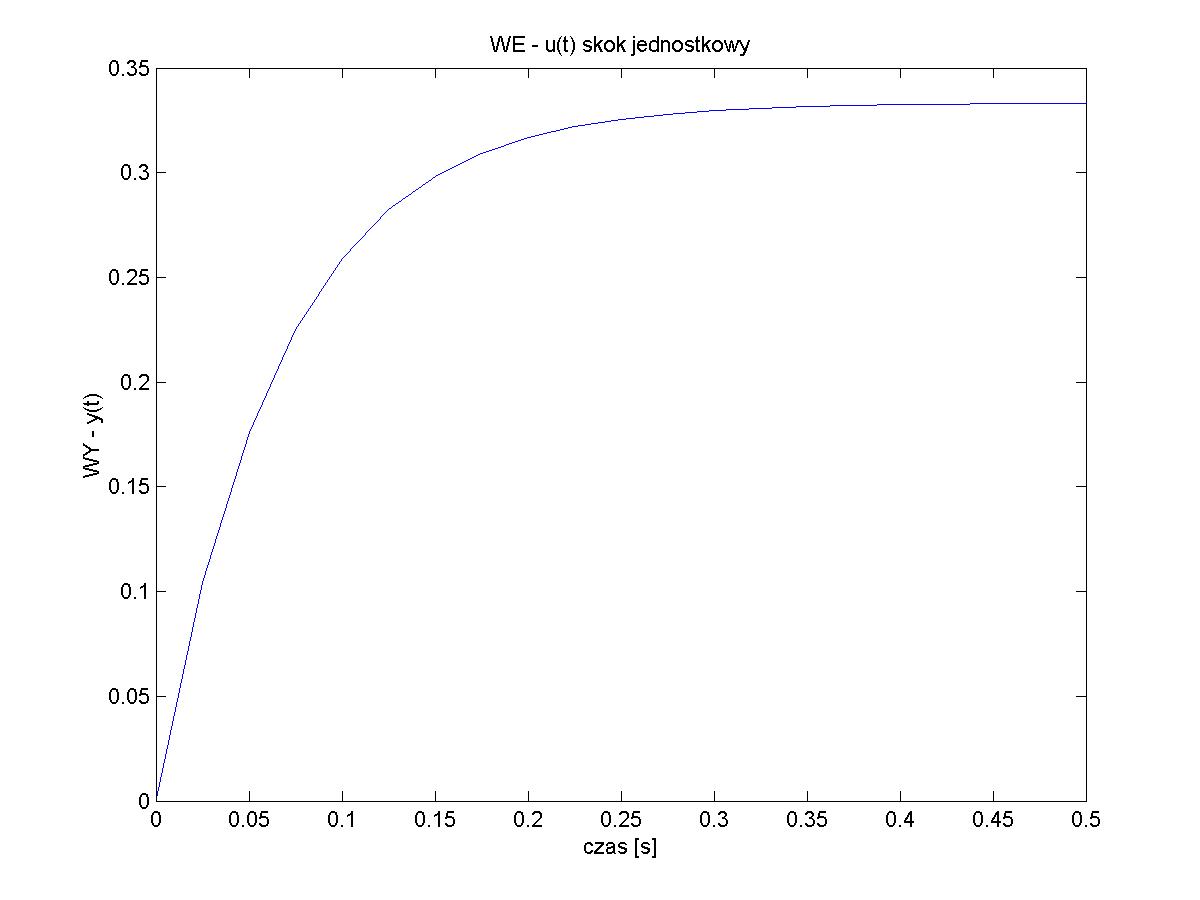
Rys.1 i Rys.2 - odpowiedzi układu na wymuszenie impulsowe i jednostkowe

Układ przy wymuszeniu jednostkowym po ustaleniu się odpowiedzi osiągnie amplitudę równą 0,333.. amplitudy wymuszenia (Wynika to bezpośrednio z twierdzenia o wartości końcowej dla badanej transmitancji). Przy wymuszeniu impulsowym odpowiedź układu dąży wykładniczo do zera. Postać obydwu przebiegów jest podyktowana tym, że przy dużym tłumieniu człony oscylacyjne zachowują się w rzeczywistości jak człony inercyjne.

u(t)

y(t)

u(t)

i(t)

y(t)

G₁(s)

G₂(s)

u(t)

y(t)

G(s)

I(t)

I₁(t)

I₂(t)

---